قوة

Forces are often described as pushes or pulls. They can be due to phenomena such as gravity, magnetism, or anything else that causes a mass to accelerate.

تعرف القوة Force في الفيزياء على أنها مؤثر يؤثر على الأجسام فيسبب تغييراً في حالته أو اتجاهه أو موضعه أو حركته. وهي نسبة تغير الزخم بالنسبة للزمن. القوى هي كميات متجهة (لها مقداراً واتجاهاً)، وتسبب في تعجيل الجسم بمقدار معين. عرف القوة أولاً أرشيميديس في القرن الثالث قبل الميلاد، ولكن إسحاق نيوتن علم بمبادئ القوة الرياضية في القرن 17. تقاس القوى بوحدة النيوتن.

حسب قانون نيوتن الثاني، لمعرفة القوة تستخدم المعادلة التالية:

القوة = الكتلة × العجلة

إذا كانت العجلة تساوي عجلة الجاذبية الأرضية (9.8 متر/ثانية)، يمكن حساب الوزن كالتالي:

الوزن = 9.8 × الكتلة

القوة هي أيضاً نسبة تغير الزخم بالنسبة للزمن:

${\vec {F}}={\mathrm {d} {\vec {p}} \over \mathrm {d} t}=m{\vec {a}}$

حيث: F = القوة، p = الزخم، t = الزمن، m = الكتلة، a = العجلة.

Aristotle famously described a force as anything which causes an object to undergo "unnatural motion"

للقوة أنواع كثيرة، منها القوة الميكانيكية التي تعمل عندما تكون الأجسام في حالة تلامس. فدفع الكرة وتحريك بدال الدراجة ينتجان عن إعمال قوة ميكانيكية، في حين أن الكهرباء والجاذبية والمغنطيسية قوى تعمل دون تلامس بين الأجسام، وتنشأ من مجال القوة. فالمجالات الكهربائية التي تنشأ حول الجسيمات المشحونة على سبيل المثال، تسبب إما تجاذبها أو تنافرها. وتتناول هذه المقالة أساسًا القوة الميكانيكية.

Though Sir Isaac Newton's most famous equation is $\scriptstyle {{\vec {F}}=m{\vec {a}}}$, he actually wrote down a different form for his second law of motion that did not use differential calculus.

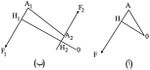
ويمكن للقوة أن تؤثر عن بعد أو عن طريق التماس، كما يمكن أن تأخذ أشكالاً مختلفة كقوة الثقالة gravitationnelle، أو الكهراكدة électrostatique، أو الكهرمغنطيسية électromagnétique أو المرنة élastique أو الهيدرودينامية hydrodynamique وغير ذلك. تتصف جميع القوى في أن لها نقطة تطبيق point d’application واتجاهاً direction وشدة intensité. ويمكن تمثيلها بشعاع أو متّجهة يعتمد طولها على سلّم القياس المختار. إن تركيب قوتين يعني استبدال قوة وحيدة تسبب الفعل ذاته بهما؛ وتسمى القوى المكافئة محصِّلة résultante. وتُجمع القوى تماماً كما تجمع الأشعة. فمجموع قوتين متلاقيتين هو قطر متوازي الأضلاع الممثِّل لهما، وكذلك فإن محصلة قوتين متوازيتين في الحالة العامة هو قوة موازية، ويبين الشكلان (1ـ ب) و(1ـ جـ) ذلك، والشروط التي يجب أن تحققها النقطة A، نقطة تطبيق المحصلة F. وقد تتساوى شدتا القوتين F1 و F2، وتتعاكسان في الاتجاه (الشكل 1ـ د) فعندئذ تكون محصلة القوتين صفراً، ويتعذر عندها تحديد موضع نقطة التطبيق A، ويقال عندئذ: إن جملة القوتين تكافئ مزدوجة couple.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 قياس القوة

A Feynman diagram for the decay of a neutron into a proton. The W boson is between two vertices indicating a repulsion.

لكي تقاس القوة يتحتم معرفة كتلة الجسم وتسارعه. وكتلة الجسم هي كمية المادة التي يحويها. وتقاس الكتلة بالكيلوجرام أو الرطل. ويصف التسارع مقدار تغير السرعة الاتجاهية للجسم ووحداته هي وحدات المسافة مقسومة على مربع وحدات الزمن. فمثلاً يمكن أن تتغير السرعة الاتجاهية للجسم بمعدل متر واحد في الثانية لكل ثانية، ويكون التسارع مترًا لكل ثانية مربعة. ويمكن أيضًا التعبير عن هذه الكمية بأنها التسارع المساوي لمتر واحد في الثانية في ثانية.

يمكن استخدام النظام المتري أو وحدات النظام الإنجليزي في قياس القوة. ففي النظام المتري يعبر عن القوة بدلالة النيوتن. والنيوتن الواحد هو القوة المطلوبة لإحداث تسارع قدره متر واحد في الثانية المربعة لجسم كتلته كيلوجرام واحد. والوحدة الأساسية للقوة في النظام الإنجليزي هي البوندال. والبوندال الواحد هو القوة المطلوبة لإحداث تسارع مقداره قدم واحدة في الثانية المربعة لجسم كتلته رطل إنجليزي واحد.

وكان العالم الفيزيائي الإنجليزي السير إسحق نيوتن هو أول من وصف العلاقة بين القوة والكتلة والتسارع، وذلك في القرن السابع عشر الميلادي. فقد نص على أن القوة الكبيرة تحدث تسارعًا أكبر مما تحدثه القوة الصغيرة، وأن تسارع الأجسام الثقيلة أقل من تسارع الأجسام الخفيفة. وقد عبر نيوتن عن العلاقة بين التسارع والقوة والكتلة بالمعادلة: ق = ك × ت. وفي هذه المعادلة ترمز (ق) للقوة المؤثرة على الجسم، (ك) لكتلته و (ت) للتسارع الذي يحدث للجسم. وتعرف هذه العلاقة بالقانون الثاني للحركة.

Galileo Galilei was the first to point out the inherent contradictions contained in Aristotle's description of forces.

 تفاعل القوى

An initially stationary object which is allowed to fall freely under gravity drops a distance which is proportional to the square of the elapsed time. An image was taken 20 flashes per second. During the first 1/20th of a second the ball drops one unit of distance (here, a unit is about 12 mm); by 2/20ths it has dropped a total of 4 units; by 3/20ths, 9 units and so on.

في أحوال كثيرة تؤثر أكثر من قوة واحدة على الجسم في الوقت نفسه. وينتج عن هذه القوى المتلاقية قوة تسمى المحصلة.

والقوة المتلاقية التي تُحدث حركة عند تفاعلها تسمى القوة غير المتوازنة. فمثلاً عندما يدفع شخصان سيارة واقفة إلى الأمام فإن مجموع القوة المبذولة تتغلب على الاحتكاك بين الطريق وإطارات السيارة، فتبدأ السيارة في التحرك إلى الأمام.

والقوة التي لا تُحدث حركة عندما تتفاعل تسمى القوة المتوازنة. فمثلاً عندما تجلس على كرسي تجذب قوة الجاذبية جسمك نحو الأرض، وفي الوقت نفسه يدفعك الكرسي إلى أعلى، بعيدًا عن الأرض. فالقوة الناشئة من الكرسي تلغي قوة الجذب وتظل في مكانك ساكنًا. ويقال عن الجسم الذي تؤثر عليه القوة المتوازنة إنه في حالة اتزان.

F_N represents the normal force exerted on the object.

 حساب القوة المحصلة

When the drag force ($F_{d}$) associated with air resistance becomes equal in magnitude to the force of gravity on a falling object ($F_{g}$), the object reaches a state of dynamical equilibrium at terminal velocity.

حساب القوة المحصلة يحتاج المرء إلى معرفة اتجاه ومقدار القوى المتلاقية. فإذا كانت هذه القوى تعمل في اتجاه واحد فإن القوة المحصلة سوف تعمل أيضًا في الاتجاه نفسه. وفي هذه الحالة يساوي مقدار القوة المحصلة مجموع مقادير القوى المتلاقية. وإن كانت هناك قوتان غير متساويتين في المقدار، وتعملان في اتجاهين متضادين، فإن القوة المحصلة تعمل في اتجاه القوة الأكبر. ويكون مقدار القوة المحصلة مساويًا للفرق بين مقداري القوتين.

ويعمل كثير من القوى المتلاقية على زاوية تقع بينها. وتستخدم كميات تسمى المتجهات (الكميات المتجهة) لحساب محصلة القوة. وفي هذه الحالة يعبر المتجه عن مقدار واتجاه القوة بسهم يشير إلى اتجاه القوة. ويعطي طول هذا السهم مقدار القوة، ويمكن اختيار أي مقياس عند رسم المتجهات. وينتهي السهم بنقطة تسمى الرأس، وتسمى النهاية المقابلة الذيل.

وهناك طرق ثلاث رئيسية لاستخدام المتجهات في تعيين القوة المحصلة: 1- طريقة متوازي الأضلاع 2-طريقة المضلع 3- الطريقة التحليلية.

أ ـ مقاييس الأوزان: يمثل وزن أي جسم قوة؛ هي قوة الثقالة، أي قوة جذب الأرض للجسم، وهي قوة تسبب التسارع ذاته g لجميع الأجسام. وينتج من القانون الأساسي للتحريك أن جسماً كتلته m يخضع إلى قوة تساوي mg هي ثقله. ويمكن تحديد قيمة g بدقة فائقة بوساطة مقياس الثقالة gravimètre، كما يمكن تحديد الأوزان بمقارنتها بكتل عيارية معلومة باستخدام الموازين.

ب ـ مقاييس القوى dynamomètres: يستخدم في مقاييس القوى التشوُّه المرن الذي يخضع له جسم صلب، وهو تشوُّه تمكن معايرته؛ ليعطي القوى المطبقة، وذلك بفضل أوزان كتل معلومة. إن معرفة قيمة g في موقع المعايرة بدقة مطلوب بالطبع، بيد أنه يكفي عادة أن تعرف قيمة g بدقة مقبولة. ولدى خضوع مقياس القوى لقوة ما يحدث تشوه في المقياس يتناسب مع هذه القوة. ففي مقاييس القوى النابضية يتشوه النابض بفعل القوة المقيسة، فيمتط، أو ينكمش بحسب تصميم المقياس، ويقاس مقدار ذلك على سلَّم مدرَّج، ويتناسب مقدار الامتطاط أو الانكماش مع القوة المقيسة.

تستخدم في مقياس القوى الصفيحي صفيحة من الفولاذ بشكل الحرف V تنزلق نهايتاها على قوس دائرة. وتقرأ القوة المطبقة على إحدى النهايتين.

وفي مقاييس القوى الحَلَقية تستخدم قطعة وحيدة دائرية أو على هيئة قطع ناقص. وهنا يؤدي تطبيق القوة إلى تقلص في القطر الخاضع للتشوه، أو تباعد في القطر الآخر العمودي عليه، ومن ثم يمكن قراءة شدة القوة المطبقة على سلَّم مدرَّج ومعاير.

ج ـ قياس الضغط: إن تطبيق قوة F على مكبس مساحته S يحتوي على سائل يولد ضغطاً P على سطح السائل، يعطى بالعلاقة. يسمى مقياس القوى من هذا النوع مقياس القوى الهيدرولي، وهو يسمح بقياس قوى شدتها عالية جداً.

كما تسمح الإفادة من المفعول الكهرضغطي الذي تخضع له صفيحة من الكوارتز بقياس القوة المؤثرة فيها عن طريق قياس الشحنة أو فرق الكمون (الجهد الكهربائي) المتولِّد بين طرفيها.

 قياس المزدوجات

 مقياس الفتل

يتألف مقياس الفتل إما من سلك فتل أو من نوابض لولبية وذلك بحسب مقدار العزم المراد قياسه. وبالمثل يمكن تحقيق ذلك بوسائل ضوئية أو ميكانيكية أو كهربائية عديدة. إحدى هذه الطرق. ويستخدم فيها مقياس تشوهjauge de contrainte مؤلف من أسلاك مقاومة. يُلصق مقياس التشوه هذا بحيث يصنع زاوية مقدارها 45 ْ مع محور العمود؛ وبحيث يشكل جسر وطسطن غير حساس بتغيرات درجات الحرارة أو بالتشوهات الطولانية. ويوصل منبع التغذية وجهاز القراءة بالنقاط التي تخضع للانزلاق.

 مكابح الامتصاص

تكبح هنا حركة المحرك المطلوب قياس عزمه بالاحتكاك الصلب، أو بالاحتكاك السائل، أو بتيارات فوكو، وتقاس القوة المطبقة على بعدٍ محدَّد والتي تؤدي إلى إيقاف المحرك عن الدوران. ويكون عزم المحرك مساوياً جداء هذه القوة ببعدها عن محور الدوران.

 طريقة متوازي الأضلاع

تستخدم في حساب محصلة قوتين فقط في كل مرة. في هذه الطريقة يُستخدم المتجهان اللذان يمثلان القوتين المتلاقيتين لرسم متوازي أضلاع. افترض مثلاً أن بين القوتين زاوية. باختيار مقياس رسم مناسب نرسم هاتين القوتين كمتجهين يلتقي ذيلاهما في نقطة واحدة. هذه النقطة تمثل الجسم الذي تعمل عليه القوتان. بعد ذلك ارسم متوازي الأضلاع بحيث يشكل المتجهان ضلعين فيه. ثم ارسم قطر المتوازي من نقطة تلاقي المتجهين إلى ركن متوازي الأضلاع المقابل، واجعل من القطر متجهًا يؤشر سهمه بعيدًا عن الجسم. يكون هذا المتجه ممثلاً للمحصلة. لتعيين مقدار المحصلة

F_k is the force that responds to the load on the spring.

 المضلع

تستخدم لتعيين المحصلة عندما تعمل أكثر من قوتين على الجسم. في هذه الطريقة تستخدم متجهات تمثل القوى المتلاقية لعمل مضلع، وترسم هذه المتجهات بالتتابع كل بعد الآخر، بحيث يكون رأس كل متجه متصلاً بذيل المتجه الذي يليه، وهكذا. ثم يرسم متجه جديد يصل رأس المتجه الأخير مع ذيل المتجه الأول. ويكون المتجه الجديد في هذه الحالة ـ والذي يكمل المضلع ـ هو الذي يمثل المحصلة. ويجب أن يكون اتجاهه بحيث يشير من ذيل المتجه الأول إلى رأس المتجه الأخير.

Relationship between force (F), torque (τ), and momentum vectors (p and L) in a rotating system.

 الطريقة التحليلية

تستخدم أيضًا لإيجاد المحصلة عندما تؤثر أكثر من قوتين على الجسم. هذه الطريقة تقوم على حقيقة أن كل متجه يمكن أن يُمثل بمحصلة متجهين صغيرين متعامدين. فعلى سبيل المثال يمكن تمثيل متجه مقداره 5 نيوتن بمتجهين متعامدين مقدارهما 4 نيوتن و 3 نيوتن. في هذا المثال يكون المتجه الذي مقداره 5 نيوتن وترًا للمثلث قائم الزاوية الذي يشكل المتجهان 4 نيوتن و3 نيوتن ضلعيه الآخرين. لذلك فإن مربع المتجه 5 نيوتن، وهو 25 يساوي مجموع مربعي المتجهين الآخرين (9 + 16).

وفي الطريقة التحليلية تمثل كل قوة متلاقية أولاً كمتجه، ويُحلّل كل من المتجهات فيما عدا واحد فقط إلى متجهين صغيرين متعامدين. ويرسم متجه من كل زوجين متعامدين موازيًا للمتجه الذي لم يُحلّل. بعد ذلك تضاف المتجهات التي تشير إلى اتجاهات متوحدة أو متعاكسة. هذه الإضافة ستؤدي في النهاية إلى زوجين من المتجهات متعامدين. ويمكن حساب محصلة هذين الزوجين حينئذ بطريقة متوازي الأضلاع. وهذه المحصلة هي محصلة القوى الأصلية المتلاقية.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 عزم القوى

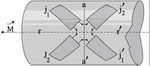
يسمى عزم القوى moment حول نقطة كما في الشكل (2) الجداء المتجه لهذه القوى ببعد النقطة عن حامل القوة. كما يعرّف عزم مزدوجة بأسلوب مماثل بالنسبة لأي نقطة. ويمثل العزم بمتجهة. ويمكن رد مجموعة قوى إلى قوة وحيدة مكافئة وإلى مزدوجة لها عزم يسمى عزماً محصّلاً moment résultant.

 القوى الأساسية

يعتبر الفيزيائيون أن جميع القوى في الكون أشكال لأربع قوى. هذه القوى الأربع مرتبة من الأضعف إلى الأقوى هي: 1- الجاذبية 2- القوة النووية الضعيفة. 3- القوة الكهرومغنطيسية 4- القوة النووية القوية. وتسمى القوة النووية الضعيفة التفاعل الضعيف والقوة النووية القوية التفاعل القوي.

وتؤثر قوة الجاذبية على مسافات طويلة في الفضاء. وهي أكثر تأثيرًا على الكتل الكبيرة. على سبيل المثال تثبت جاذبية الشمس الأرض في مدارها. وتعمل القوة الكهرومغنطيسية على مسافة أقل بكثير من مدى قوة الجاذبية. وهي تحفظ الجزيئات متماسكة. وتؤثر القوى النووية الضعيفة والقوية داخل نويات الذرات.

 قانون التحريك الأساسي

ينص قانون التحريك الأساسي في الميكانيك على أنه إذا خضع جسم كتلته m إلى قوة فإنه يكتسب تسارعاً ويكون. تقاس F في الجملة الدولية بالنيوتن، ويرمز له بـ N؛ وهو بالتعريف القوة التي إذا أثرت في كتلة مقدارها كيلوغرام واحد سببت تسارعاً قدره 1م/ثا2، ولا توجد تسمية لعزم المزدوجة، وإنما تقاس بواحدة هي جداء واحدة طول بواحدة قوة أي بواحدة نيوتن ـ متر.

==

 المصادر

الموسوعة المعرفية الشاملة

 أنظر أيضا

• central force
• Modified Newtonian dynamics

 ببليوگرافيا

• Corbell, H.C. (1994). Classical Mechanics p 28,. New York: Dover publications. ISBN 0-486-68063-0. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Cutnell, John d. (2004). Physics, Sixth Edition. Hoboken, NJ: John Wiley & Sons Inc. ISBN 041-44895-8. {{cite book}}: Check |isbn= value: length (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Feynman, R. P., Leighton, R. B., Sands, M. (1963). Lectures on Physics, Vol 1. Addison-Wesley. ISBN 0-201-02116-1.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Halliday, David (2001). Physics v. 1. New York: John Wiley & Sons. ISBN 0-471-32057-9. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Parker, Sybil (1993). Encyclopedia of Physics, p 443,. Ohio: McGraw-Hill. ISBN 0-07-051400-3.
• Sears F., Zemansky M. & Young H. (1982). University Physics. Reading, MA: Addison-Wesley. ISBN 0-201-07199-1.
• Serway, Raymond A. (2003). Physics for Scientists and Engineers. Philadelphia: Saunders College Publishing. ISBN 0-534-40842-7.
• Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.
• Verma, H.C. (2004). Concepts of Physics Vol 1 (2004 Reprint ed.). Bharti Bhavan. ISBN 81-7709-187-5.

 وصلات خارجية

• Video lecture on Newton's three laws by Walter Lewin from MIT OpenCourseWare
• A Java simulation on vector addition of forces
• Force Unit Converter