مرونة

ميكانيكا الاستمرارية

الحفاظ على الكتلة الحفاظ على العزم معادلات ناڤييه–ستوكس الميكانيكا الكلاسيكية إجهاد · إنفعال · Tensor ميكانيكا الجوامد صلب· المرونة اللدونة · قانون هوك Rheology · مرونة لزجة ميكانيكا الموائع الموائع · استاتيكا الموائع ديناميكا الموائع · لزوجة · موائع نيوتونية موائع غير نيوتونية شد سطحي العلماء نيوتن · ستوكس · كلود-لوي ناڤييه · كوشي· هوك · غيرهم

رسم توضيحي للدونة

المرونة Elasticity هى خاصية الأجسام التى لها القدرة على الرجوع إلى شكلها و أبعادها الأصلية بعد تشكيلها ، أى: عدم بقاء الجسم على الشكل الذى تشكل به بعد زوال الحمل المؤثر و رجوعه إلى شكله الأصلى .

إن المرونة هي الخاصية التي تمتلكها بعض الأجسام للعودة إلى هيئتها وأشكالها الأصلية بعد التوقف من تأثير القوة التي أدت إلى التغيير في أشكالها.

فلنأخذ سلكين أحدهما من الصلب والآخر من الألمونيوم ملفوفين بصورة حلزونية (على شكل زنبرك).

فنلاحظ تمدد وتشوه السلكين عند جذبهما بلطف.

ونلاحظ عند إفلاتهما أن السلك الفولاذي يعود إلى وضعه وشكله الأصليين، بينما يبقى السلك المصنوع من الألمونيوم على هيئته المشوهة.

مما يعني أن الفولاذ (الصلب) يمتلك خاصية المرونة على عكس حال الألمونيوم؛ والمرونة هي تحول قابل للانعكاس.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 قابلية التشكيل (الطواعية)

إن معظم المواد تكون قابلة للتشكيل حسب الضغوط (القوى) التي تتعرض لها؛ ورجوعا إلى مثال السلك الفولاذي يمكن تغيير شكله هذه المرة بطريقة غير قابلة للانعكاس عند جذبه بقوة أكبر من المرة السابقة وبالتالي يحتفظ السلك بهيئته الجديدة حتى بعد التخلص من الضغط (عند إفلاته) وهذه هي خاصية الطواعية (التحول غير القابل للانعكاس) والتي تناقض خاصية المرونة والتى تسمى بخاصية اللدونة والتى يجب أن نفرق بينها وبين المرونةفالدونة هى قابلية الجسم للتشكل

 الانفعال

هو استجابه الجسم النسبية للإجهاد المؤثر.

• الانفعال الطولي هو التغيير في الطول بالنسبه للطول الأصلي.
• الانفعال الحجمي هو التغير في حجم الجسم بالنسبه للحجم الاصلي.
• انفعال القص

 قانون هوك

يتناسب الانفعال تناسبا طرديا مع الاجهاد المؤثر من بدايه التحميل إلى حد معين يسمى بحد المرونه اى ان النسبه بين الاجهاد و الانفعال = مقدار ثابت و يسمى ثابت التناسب بمعامل المرونه.

 العلاقة بين الإجهاد والتشوه

يعنى مهندسو الإنشاءات بتحليل حالة الإجهادات في البنية الإنشائية، حيث يصعب قياس حالة الإجهادات مباشرة، إنما يمكن قياس حالة التشوهات والسعي إلى صياغة علاقة بين الإجهادات والتشوهات. تسمى هذه العلاقة بالمعادلة الأساسية، ويعدّ قانون هوك العام المعادلة الأكثر شيوعاً التي تعبر عن علاقة خطية بين الإجهاد والتشوه على النحو الآتي: σij= Cij εkl حيث يسمى Cijkl موتر المتانة (الجسأة) stiffness الذي يعبر عن مقاومة المادة للتشوه. يمثل هذا القانون ست معادلات تربط بين الإجهاد والتشوه ويعطى الإجهاد σ23 على سبيل المثال وفق العلاقة:

σ23 = C2311 ε11+ C2312 ε12 + C2313 ε13+ C2322 ε22+ C2323 ε23+ C2333 ε33

تمثل الثوابت Cijkl موتراً من الدرجة الرابعة يتضمن 36 مركبة بدلاً من 81، ويعود ذلك إلى تناظر كل من موتر الإجهادات σij وموتر التشوهات εij. من جهة أخرى، يتميز موتر المتانة Cijkl بخاصة التناظر (Cijkl = C klij)، وهذا ما يخفض عدد المركبات إلى 21 في موتر المتانة. ينطبق ذلك على المواد عديمة التناظر، أما المواد التي تمتلك خواص تناظر، فإن عمليات التناظر تسهم في تقليل عدد مركبات موتر المتانة. فمن أجل جسم متماثل المناحي isotrope حيث تتساوى ثوابت المتانة في كل الاتجاهات، يقتصر موتر المتانة على ثابتين فقط؛ هما معامل المرونة E وثابت بواسون uυ ويُشتق منهما ثابتا لامي λ Lamé وμ حيث:

يمكن أيضاً صياغة قانون هوك بحيث تعطى التشوهات بدلالة الإجهادات: εijkl = Sijkl σkl حيث يسمى Sijkl موتِّر المطاوعة compliance الذي يشترك - من أجل المادة نفسها - مع موتر المتانة في عدد المركبات ومنهجية التعامل، ويختلفان في الواحدة (واحدة ثوابت موتر المطاوعة هي مقلوب واحدة ثوابت موتر المتانة).

 نظرية المرونة

تقتصر خاصة المرونة على إجهادات محدودة أصغر من حد المرونة σE الذي يترافق في معظم المواد مع تشوهات صغيرة. من هنا اقترن تعبير المرونة بنظرية أساسية تسمى نظرية المرونة theory of elasticity التي تعنى بدراسة التشوهات الصغيرة والمستمرة والعكوسة للأجسام المرنة والمتجانسة.

تستند نظرية المرونة إلى عمومية قانون هوك وإلى مبدأ الجمع الذي ينص على أن محصلة التشوهات الناجمة عن مجموعة قوى تساوي مجموع التشوهات الناجمة عن كل منها. تتناول نظرية المرونة تحليل الإجهادات والتشوهات في كل نقطة من الجسم المعرض لجملة من القوى، كما تسعى إلى إنقاص عدد المعاملات أو الثوابت في المعادلات التي تربط بين الإجهادات والتشوهات بالاعتماد على عمليات التناظر التي تتميز بها المادة.

الشكل (3)

 مفهوم الإجهاد

هو القوة المؤثرة على وحدة المساحات P=F/A

تتعرض المواد والعناصر الإنشائية والبنى عند التشكيل forming أو الاستخدام أو الراحة لعدد من القوى أو الأحمال التي تسهم مع عوامل أخرى في تحديد أدائها وسلوكها وشروط انهيارها fracture وفترة خدمتها. وينتج من هذه القوى ما يطلق عليه إجهادات التحميل loading stress. لكن غياب القوى الخارجية لا يعني بالضرورة انعدام الإجهادات في الأجسام وذلك بسبب قوى الجاذبية أو القوى المغنطيسية التي ينتج منها ما يسمى الإجهادات الذاتية. ومهما كانت طبيعة هذه القوى؛ فهي تسبب حركة الأجسام المعرضة لها، أو تشوهها.

عندما يتعرض جسم إلى قوة خارجية فإنها تؤثر في سطحه، وينتقل تأثيرها إلى داخله؛ لأن كل عنصر حجم يؤثر في العنصر المجاور. تتعامل نظرية المرونة مع مفهوم الإجهاد σ الذي يعبر عن القوة في واحدة السطح (σ = F/S) S. وحيث يمكن تقسيم متجه القوةF^→∆ المؤثرة في سطح إلى مركبة ناظمية F^{→</supn>∆ومركبة مماسية F→</supt>∆(الشكل -3)، فإذا كانت القوة ناظمية، يقال: إن الإجهاد ناظمي σ، وإذا كانت مماسية، يقال: إنه إجهاد قص τ. إن التوصيف الكامل للإجهادات المؤثرة يتطلب ليس فقط تحديد قيم القوى المؤثرة واتجاهاتها؛ وإنما أيضاً اتجاهات السطوح المعرضة للقوى؛ لأن تغير اتجاه السطح يؤدي إلى تغير مركبات القوة وبالنتيجة الإجهاد المؤثر فيه. بناءً على ذلك، يصبح التعريف العام للإجهاد على النحو الآتي:}

حيث يشير j إلى محور الإحداثيات الموازي للقوة

وi إلى محور الإحداثيات العمودي على السطح ∆Si.

بتعبير آخر: من أجل قوة محددة الاتجاه والمقدار، يتعلق الإجهاد في نقطة معينة بإحداثيات موقعها واتجاهي متجه القوة والمتجه الناظمي على السطح المعتبر المار من هذه النقطة. من هنا يشكل مفهوم الإجهاد كياناً رياضياً يربط بين متجه القوة المطبق على سطح ما والمتجه الناظمي عليه. وباعتبار المتجهات موترات من الدرجة الأولى، تكون الإجهادات من الطبيعة الرياضية نفسها ويمثل الإجهاد σij موتراً من الدرجة الثانية يتضمن، في جملة إحداثيات ثلاثية الأبعاد، تسع مركبات للإجهاد، ثلاث منها ناظمية σii وست مماسية τii.

 مفهوم التشوه

تتشوه الأجسام بفعل القوى التي تتعرض لها، ويحصل التشوه نتيجة انتقال المادة وما ينجم عنه من تغير في الطول أو التواء ناتج من تغير في الزوايا. يعرف انتقال نقاط المادة ضمن جملة إحداثيات (xyz) بوساطة متجه الانتقال ، الذي يتعلق بإحداثيات النقطة ، ومركباته (uvw). فإذا عددنا قطعة مستقيمة تصل بين نقطتين A وB من جسم صلب يتعرض للتشوه، تصبح هذه القطعة بعد التشوه B' A' ويكون تشوهها النسبي

إذا كان ε موجباً، نتحدث عن استطالة، وإذا كان سالباً، نتحدث عن تقلص. وبما أن انتقال النقطتين AوB يتعلق بإحداثيات كل منهما، فإن B' A' ليس بالضرورة موازياً لـ AB، وتسمى الزاوية بين اتجاه AB واتجاه 'B' A بالانتقال الزاوي. من هنا يصبح التشوه مرتبطاً باتجاه انتقال النقطة (اتجاه التغير في الطول) واتجاه الطول الأصلي، فعندما يكون الاتجاهان متطابقين، نتحدث عن تشوه طولي (شد، انضغاط، تمدد، تقلص)، وعندما يتعامدان، نتحدث عن تشوه قص shear deformation.

في حالة أحادية البعد على المحور ox، فإن استطالة قطعة مستقيمة صغرية AB طولها dx تساوي الفرق بين انتقال النقطة B وانتقال النقطة A. فإذا كان انتقال النقطة A يساوي uA، فإن انتقال النقطة B سيكون

أما التشوه النسبي فهو

وبالطريقة نفسها يكون التشوه النسبي للقطعة نفسها إذا كانت على المحور oy أو oz مساوياً إلى

على الترتيب.

الشكل (4)

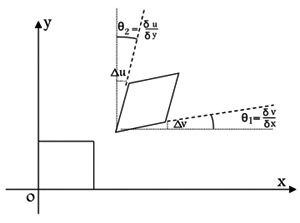
في حالة تشوه القص، يمكن عد تشوه مربع صغري توازي أضلاعه محوري الإحداثيات في المستوي xoy يتحول بفعل تشوه القص إلى معين تميل أضلاعه بزاويتين صغريتين θ1 وθ2 على كل من المحورين ox وoy (الشكل-4). يعرف تشوه القص بالعلاقة:

وبعدّ الزاويتين θ1 وθ2 صغيرتين، يكون:

ويعطى تشوه القص للمربع وفق الاتجاهين ox وoy بالعلاقة :

حيث (uv) تمثل مركبات شعاع الانتقال في المستوي xoy.

بناءً على ذلك يعطى التشوه عموماً بالعلاقة

فإذا تطابق اتجاه التشوه مع اتجاه الطول الأصلي، كان التشوه طولياً

وإذا اختلفا، كان تشوه القص

ينتج التشوه εij من العلاقة بين متجه الانتقال

ومتجه الطول الأصلي، لهذا يعدّ التشوه εij موتراً من الدرجة الثانية يتميز بالتناظر لأن εij = εji.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 السلوك الميكانيكي المرن

عند تطبيق قوةF^→ على جسم ومراقبة التشوه ε، يقال إن الجسم يتمتع بقدر من المرونة عندما يتناقص التشوه بمجرد تناقص القوة (الـشكل-1 أ-). إذا تطـابق منحني التحميل المرافق لزيادة القـوة(F^→,ε) مع المنحني (F^→,ε) المرافق لتناقص القوة، يقال: إن المرونة كاملة، أو مثالية، وإن العلاقة F = f (ε) تمكن من تحديد القوة بمجرد معرفة التشوه وبالعكس (الشكل -1 ب-)؛ وإن المادة لا تحتفظ بتشوه دائم، وإنما تعود إلى أبعادها وشكلها الابتدائيين. عندما تكون العلاقة F = f (ε) خطية (الشكل -1 جـ -)؛ تصبح المرونة كاملة وخطية F = k ε حيث يمثل k ثابتاً يميز المادة. أما إذا احتفظ الجسم - بعد تحميله قوة تفوق عتبة معينة وإزالة هذه القوة - بتشوه دائم؛ فيقال: إنه يتميز بسلوك لدن (الشكل -1 أ -).

الشكل (1)

أما ما يتعلق بالسلوك اللزج لبعض الأجسام، مثل السوائل والبوليميرات polymers والمعادن عند درجات الحرارة العالية؛ فيتم توصيف السلوك من خلال علاقة تربط بين معاملات القوى ومعاملات سرعة التشوه؛ أي مشتق التشوه بدلالة الزمن e واللزوجة η.

يستنتج مما سبق أن المرونة سمة تصف السلوك الميكانيكي للمواد كاملاً أو جزئياً وفق استجابتها لفعل القوى المؤثرة فيها.

 توصيف السلوك المرن - اختبار الشد

يعدّ اختبار الشد tensile test من أكثر الاختبارات شيوعاً لتوصيف السلوك الميكانيكي للمواد، ويتضمن هذا الاختبار إخضاع عينة أسطوانية أو موشورية محددة الأبعاد والشكل لقوة متزايدة موازية لمحورها حتى انهيارها وتسجيل منحني زيادة القوةF^→ بدلالة زيادة التشوه (استطالة العينة) (F^→,ε). تسمح دراسة هذا المنحني باستنتاج سلوك المادة المدروسة وتحديد عدد من المواصفات الميكانيكية المهمة في التطبيقات الهندسية. ولاختلاف أشكال العينات وأبعادها، ومن أجل معايرة منهجية الدراسة؛ يتم عموماً - بالاعتماد على تجانس توزيع القوى على سطح مقطع عينة الشد - استخدام مفهوم الإجهاد stress الذي يعبر عن القوة المطبقة على واحدة السطح والتشوه النسبي strain الذي يعبر عن استطالة واحدة الطول. فعندما تتعرض عينة سطح مقطعها S وطولها الابتدائي L لقوة شد F^→ موازية لمحورها؛ يكون الإجهاد الناظمي σ المطبق على سطح مقطعها العمودي على اتجاه القوة مساوياً إلى σ = F/S ويكون التشوه النسبي ε الناجم عن استطالة قدرها ∆L مساوياً إلى ε = (∆L/L) x 100. يسمح ذلك بتحويل المنحني (F^→,ε) إلى منحني إجهاد- تشوه (σ, ε) يتميز بالعمومية التي لا تتعلق بأبعاد العينة. يعطي (الشكل -2) عدة نماذج من منحنيات الشد الممثلة لعدد من المواد التي تظهر أنماطاً مختلفة في سلوكها الميكانيكي.

يبين منحني الشد للمواد القَصِفة brittle، مثل المواد الزجاجية والسيراميكية (الشكل -2 ب -) السلوك المرن المتميز لهذه المواد حيث يزداد الإجهاد خطياً بدلالة التشوه حتى الانهيار الذي يحصل عند إجهاد الكسر σ1 دون إنذار مسبق ودون أي تشوه دائم. فإذا أزيلت قوة التحميل F^→ من أجل إجهاد σ أصغر من σ1، تناقص منحني الإجهاد - تشوه على منحني التحميل نفسه، وعادت العينة إلى أبعادها الابتدائية. يُعدّ روبرت هوك Robert Hooke مابين(1635-1703) من الرواد الأوائل في علم الميكانيك ودراسة السلوك الميكانيكي للمواد، وينسب إليه قانون التناسب بين الإجهاد σ والتشوه ε في المواد ذات السلوك المرن (قانون هوك):

σ = F/S = E ∆L/L = Eε

حيث يشير E إلى معامل المرونة elastic modulus أو معامل يونغYoung مابين(1773-1829) الذي يساوي ميل المنحني الخطي إجهاد - تشوه.

يبين منحني الشد للمواد اللدنة - مثل المعادن وسبائكها (الشكل -2 جـ)- أن السلوك الميكانيكي لهذه المواد هو سلوك مركب يتضمن عدة مراحل متميزة. في المرحلة الأولى، يكون التشوه مرناً ما بقي الإجهاد أصغر من حد المرونة σE، فإذا تعرضت عينة الشد إلى إجهاد σ أصغر من σE، وأزيل هذا الإجهاد؛ عادت العينة إلى أبعادها الابتدائية. أما إذا تجاوز الإجهاد حد المرونة دون بلوغ إجهاد الكسر σf، فإن إزالة الإجهاد تسبب تعرض العينة إلى تشوه دائم. وكما أشير سابقاً، يعطي ميل المنحني إجهاد - تشوه في المنطقة الخطية معامل المرونة E للمادة المدروسة.

الشكل (2)

يتميز منحني الإجهاد - تشوه لمادة مطاطية (الشكل -2د) بصغر حد المرونة σE وصغر معامل المرونة E وارتفاع التشوه النسبي قبل الانهيار وعنده (100 - 1000٪) ويعود ما يشاع عن تميز مرونة المطاط إلى قابليته العالية للتشوه العكوس بفعل إجهادات صغيرة مع أن قسماً كبيراً من هذا التشوه لا يتسم بالسلوك المرن.

يشير قانون هوك إلى ارتباط التشوه بخواص المادة ولاسيما معامل المرونة وإلى استقلال الإجهاد عنها وارتباطه بأبعاد الجسم ولاسيما السطح المطبق عليه (سطح مقطع عينة الشد).

يرتبط معامل المرونة E مباشرة بالمرونة (السلوك الميكانيكي المرن)، فكلما كان E كبيراً، ازدادت المقاومة الميكانيكية؛ أي صغر التشوه، وازدادت عتبة إجهاد حد المرونة σE الذي يبدأ بعده التشوه اللدن. وكلما كان E صغيراً؛ ازدادت قابلية التشوه بفعل قوى أو إجهادات صغيرة.

تصنف المواد التي تنسجم مع قانون هوك ضمن المواد المرنة والخطية المرفقة. وإذا كانت كل مادة مرنة ليست خطية بالضرورة؛ فإن كل مادة خطية السلوك ليست بالضرورة مرنة؛ لأن استجابتها للإجهاد قد لا تكون آنية (المواد المرنة اللزجة، مثل البوليميرات والمعجونة والمعلقات ).

يشير تعبير المرونة إلى نمط من أنماط السلوك الميكانيكي لعدد من الأجسام الصلبة التي تتشوه تحت تأثير الإجهادات على نحو آني ومرن وعكوس حيث يتناسب التشوه مع الإجهادات المطبقة وينعدم تماماً وآنياً بمجرد زوالها طالما بقيت هذه الاجهادات أصغر من قيمة حدية تسمى حد المرونة σE.

 معامل المرونة

 معامل يونج

إذا ثبت سلك من أحد طرفيه و جذب من الطرف الآخر بقوة F عمودية على مساحة مقطعه A₀ و زاد طوله الاصلى L₀ بمقدار ΔL فأن معامل يونج و يرمز له بالرمز Y و يعرف بإنه النسبة بين الاجهاد و الانفعال و يعطى بالعلاقة الآتية :

$Y\equiv {\frac {\mbox{tensile stress}}{\mbox{tensile strain}}}={\frac {\sigma }{\varepsilon }}={\frac {F/A_{0}}{\Delta L/L_{0}}}={\frac {FL_{0}}{A_{0}\Delta L}}$

 معامل المرونه الحجمى

توجد الاجسام عادة تحت تأثير الضغط الجوى P_{0 و بالتالى فإن أبعاد هذه الاجسام تكون مقاسة تحت تأثير الضغط الجوى, و لكن إذا أثرنا بقوة منتظمة F على جسم مساحته A0 فإنه سوف ينشأ زيادة في الضغط مقدارها Δp و يصير الضغط الواقع على الجسم في هذه الحالة P0+Δp و يحدث تغيرا في ابعاد الجسم. في هذه الحالة يكون الجسم تحت تأثير إجهاد}

• معامل الصلابه

 المرونة الضوئية

الشكل (5)توزع الإجهادات ضمن عينة ذات فتحة مستديرة

تهدف المرونة الضوئية photoelasticity إلى تمثيل حالة الإجهادات في بنية ميكانيكية حقيقية وتفحّصها؛ وذلك عبر إخضاع نموذج شفاف مصغر لهذه البنية لحالة إجهادات مماثلة واستخدام ظاهرة الانكسار المضاعف المحرضة بفعل الإجهاد في مادة النموذج لدراسة توزع هذه الإجهادات فيه. ولدى مرور حزمة من الضوء المستقطب ضمن النموذج يتم الحصول على مجموعة من أهداب التداخل (الشكل -5) التي تتعلق بالإجهادات المطبقة في كل نقاط النموذج وتسمح بتحديد شدة هذه الإجهادات واتجاهاتها. تتميز طريقة المرونة الضوئية بإمكانية توفير تمثيل مجسم لحالة الإجهادات وتقييم شكل البنية وأبعادها ونقاط الضعف المحتملة قبل استنتاج المعطيات الرقمية.

 التوجهات المعاصرة في مجال المرونة

ما تزال نظرية المرونة تشكل العمود الفقري لميكانيك الجسم الصلب وتطبيقاته المتعددة. وتتمحور تطبيقات المرونة الراهنة حول اتجاهات مختلفة من أبرزها:

• هندسة الميكانيك الإنشائي،
• دراسة الخواص الميكانيكية للمواد والأجسام الصلبة ونمذجتها،
• الجيوفيزياء وتفسير المعطيات السيزمية،
• الفحص اللاإتلافي للمواد والبنى،
• البيوميكانيك (ميكانيك الأعضاء الحية) وتوصيف النسج الطرية (الشرايين والأربطة و…)،
• مرونة المطاطيات ودراسة حالات اللامرونة والمرونة اللاخطية،
• المرونة الحرارية thermoelasticity والمرونة المغنطيسية اللاخطية nonlinear magnetoelasticity،
• السلوك الميكانيكي لأغشية الترشيح وميكانيك الأغشية الرقيقة،
• ميكانيك الكسر fracture mehanics.

 انظر أيضا

• لدونة
• Stiffness
• Elastic modulus
• Linear elasticity
• Pseudoelasticity
• مرونة لزجة

 المصادر

• W.J. Ibbetson (1887), An Elementary Treatise on the Mathematical Theory of Perfectly Elastic Solids, McMillan, London, p.162
• L.D. Landau, E.M. Lifshitz (1986), Course of Theoretical Physics: Theory of Elasticity Butterworth-Heinemann, ISBN 0-7506-2633-X
• J.E. Marsden, T.J. Hughes (1983), Mathematical Foundations of Elasticity, Dover, ISBN 0-486-67865-2
• P.C. Chou, N. J. Pagano (1992), Elasticity: Tensor, Dyadic, and Engineering Approaches, Dover, ISBN 0-486-66958-0
• R.W. Ogden (1997), Non-linear Elastic Deformation, Dover, ISBN 0-486-69648-0

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مراجع للاستزادة

• S. TIMOSHENKO & J.N. GOODIER, Theory of Elasticity (McGraw-Hill, N. Y. 1951).
• L.D. LANDAU & E. M. LIFSCHITZ, Theory of Elasticity (Pergamon Press, England 1986).
• ARTHUR BORESI & KEN. P. CHONG, Elasticity in Engineering Mechanic, (Wiley, N. Y. 1999).