مرباع
في علم الرياضيات يشار إلى المرباع أو الكواترنيون إنگليزية: Quaternion بأنه امتداد عملية غير تبديلية للأعداد العقدية. تم وصف الكواترنيون من قبل السير وليام روان هاملتون في عام1843 وطبقهم على الميكانيك في الفضاء الثلاثي الأبعاد. في البداية تم اعتبار الكواترنيون كعنصر غير مفيد لأنها تخالف قانون العملية التبديلية ab = ba. على الرغم أنه تم الاستعاضة عنهم في كثير من التطبيقات بالأشعة والمصفوفات، إلا ما زال يوجد لهم العديد من الاستخدامات في الرياضيات النظرية والتطبيقية، بشكل خاص الحسابات المتعلقة بالدوران الثلاثي الأبعاد كما في الرسوميات الحاسوبية الثلاثية الأبعاد.
في العصر الحديث يشار إلى الكواترنيون بالرمز الجبري H نسبة إلى العالم وليام روان هاملتون أو باستخدام الرمز العريض .
التاريخ

* هنا وبينما كان سائراً
في السادس عشر من اكتوبر 1843،
اكتشف السير وليام روان هاملتون،
في ومضة عبقرية،
الصيغة الأساسية
لضرب الكواترنيونات
i² = j² = k² = i j k = −1
ونقشها على حجر في هذا الجسر
الجبر الكواترنيوني قدمه عالم الرياضيات الأيرلندي السير وليام روان هاملتون في 1843.[1] إلا أن استخدام الكواترنيونات لوصف انعدالات جسم صلب كان له تاريخ أقدم بكثير يعود على الأقل إلى 1776 في عمل[2] اويلر.
التعريف
تعرف الكواترنيون على شكل حلقة
وتكون عملية الجمع على الشكل التالي:
وعملية الطرح كما يلي:
وباستخدام قانون التوزيع وتطبيق العلاقات المعرفة ينتج لدينا:
بحيث أن كل كواترنيون هي علاقة خطية حقيقية متفردة للزمر الرباعية الأساسية 1, i, j, k.
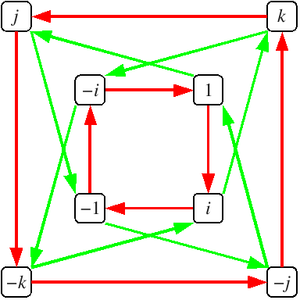
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
الخصائص الجبرية
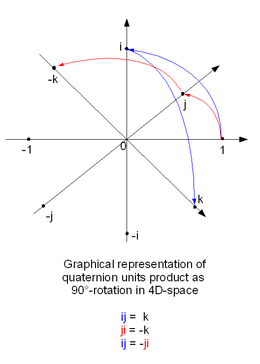
الجداء البسيط
من أجل أي كواترنيون تعطى الصيغ الأساسية لجداء عوامل الكواترنيون على الشكل التالي:
حيث i, j, k وتلخص جداءات العناصر الرئيسية للكواترنيونات في الجدول التالي:
على سبيل المثال: بما أن
فإن حاصل الجداء اليميني لكلا طرفي المعادلة بـ k يعطي:
وبمثل هذه الطريقة يتم الحصول على كامل جدول الضرب. على خلاف جداء الأعداد الحقيقية أو العقدية، فإن جداء الكواترنيون ليس عملية تبديلية مثلاً , بينما . إن الخاصة اللاتبديلية لجداء الكواترنيون له خصائص غير متوقعة، مثلاً فإن المعادلات متعددة الحدود الممثلة على شكل كواترنيونات من الممكن أن يكون لها عدد حلول فريدة أكثر من درجة المعادلة. مثلاً المعادلة
تملك عدد حلول لانهائي للكواترنيون تعطى بالعلاقة
حيث
حيث تمثل مجموعة الحلول كرة واحدية متمركزة في الفضاء العقدي الثلاثي الأبعاد الذي هو فضاء جزئي من فضاء الكواترنيون، وتقطع هذه الكرة المستوي العقدي فقط عند قطبيها و.
انظر أيضاً
- 3-sphere
- Associative algebra
- Biquaternion
- Clifford algebra
- عدد عقدي
- Conversion between quaternions and Euler angles
- Division algebra
- Dual quaternion
- زوايا اويلر
- Exterior algebra
- الجبر الهندسي
- Hurwitz quaternion
- Hurwitz quaternion order
- Hyperbolic quaternion
- Hypercomplex number
- Octonion
- Quaternion group
- مصفوفة كواترنيونية
- Quaternions and spatial rotation
- Rotation operator (vector space)
- Slerp
- SO(4)
- Split-quaternion (Coquaternion)
- Tesseract
- Olinde Rodrigues
- وليام روان هاملتون
الهامش
وصلات خارجية ومصادر
كتب ومطبوعات
- Hamilton, William Rowan. On quaternions, or on a new system of imaginaries in algebra. Philosophical Magazine. Vol. 25, n 3. p. 489-495. 1844.
- Hamilton, William Rowan (1853), "Lectures on Quaternions". Royal Irish Academy.
- Hamilton (1866) Elements of Quaternions University of Dublin Press. Edited by William Edwin Hamilton, son of the deceased author.
- Hamilton (1899) Elements of Quaternions volume I, (1901) volume II. Edited by Charles Jasper Joly; published by Longmans, Green & Co..
- Tait, Peter Guthrie (1873), "An elementary treatise on quaternions". 2d ed., Cambridge, [Eng.] : The University Press.
- Michiel Hazewinkel, Nadiya Gubareni, Nadezhda Mikhaĭlovna Gubareni, Vladimir V. Kirichenko. Algebras, rings and modules. Volume 1. 2004. Springer, 2004. ISBN 1-4020-2690-0
- Maxwell, James Clerk (1873), "A Treatise on Electricity and Magnetism". Clarendon Press, Oxford.
- Tait, Peter Guthrie (1886), "Quaternion". M.A. Sec. R.S.E. Encyclopaedia Britannica, Ninth Edition, 1886, Vol. XX, pp. 160-164. (bzipped PostScript file)
- Joly, Charles Jasper (1905), "A manual of quaternions". London, Macmillan and co., limited; New York, The Macmillan company. LCCN 05036137 //r84
- Macfarlane, Alexander (1906), "Vector analysis and quaternions", 4th ed. 1st thousand. New York, J. Wiley & Sons; [etc., etc.]. LCCN es 16000048
- 1911 encyclopedia: "Quaternions".
- Finkelstein, David, Josef M. Jauch, Samuel Schiminovich, and David Speiser (1962), "Foundations of quaternion quantum mechanics". J. Mathematical Phys. 3, pp. 207-220, MathSciNet.
- Du Val, Patrick (1964), "Homographies, quaternions, and rotations". Oxford, Clarendon Press (Oxford mathematical monographs). LCCN 64056979 //r81
- Crowe, Michael J. (1967), A History of Vector Analysis: The Evolution of the Idea of a Vectorial System, University of Notre Dame Press. Surveys the major and minor vector systems of the 19th century (Hamilton, Möbius, Bellavitis, Clifford, Grassmann, Tait, Peirce, Maxwell, Macfarlane, MacAuley, Gibbs, Heaviside).
- Altmann, Simon L. (1986), "Rotations, quaternions, and double groups". Oxford [Oxfordshire] : Clarendon Press ; New York : Oxford University Press. LCCN 85013615 ISBN 0-19-855372-2
- Altmann, Simon L. (1989), "Hamilton, Rodrigues, and the Quaternion Scandal". Mathematics Magazine. Vol. 62, No. 5. p. 291-308, Dec. 1989.
- Adler, Stephen L. (1995), "Quaternionic quantum mechanics and quantum fields". New York : Oxford University Press. International series of monographs on physics (Oxford, England) 88. LCCN 94006306 ISBN 0-19-506643-X
- Trifonov, Vladimir (1995), "A Linear Solution of the Four-Dimensionality Problem", Europhysics Letters, 32 (8) 621-626, DOI: 10.1209/0295-5075/32/8/001
- Ward, J. P. (1997), "Quaternions and Cayley Numbers: Algebra and Applications", Kluwer Academic Publishers. ISBN 0-7923-4513-4
- Kantor, I. L. and Solodnikov, A. S. (1989), "Hypercomplex numbers, an elementary introduction to algebras", Springer-Verlag, New York, ISBN 0-387-96980-2
- Gürlebeck, Klaus and Sprössig, Wolfgang (1997), "Quaternionic and Clifford calculus for physicists and engineers". Chichester ; New York : Wiley (Mathematical methods in practice; v. 1). LCCN 98169958 ISBN 0-471-96200-7
- Kuipers, Jack (2002), "Quaternions and Rotation Sequences: A Primer With Applications to Orbits, Aerospace, and Virtual Reality" (reprint edition), Princeton University Press. ISBN 0-691-10298-8
- Conway, John Horton, and Smith, Derek A. (2003), "On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry", A. K. Peters, Ltd. ISBN 1-56881-134-9 (review).
- Kravchenko, Vladislav (2003), "Applied Quaternionic Analysis", Heldermann Verlag ISBN 3-88538-228-8.
- Hanson, Andrew J.[1] (2006), "Visualizing Quaternions", Elsevier: Morgan Kaufmann; San Francisco. ISBN 0-12-088400-3
- Trifonov, Vladimir[2] (2007), "Natural Geometry of Nonzero Quaternions", International Journal of Theoretical Physics, 46 (2) 251-257, DOI: 10.1007/s10773-006-9234-9
- Ernst Binz & Sonja Pods (2008) Geometry of Heisenberg Groups American Mathematical Society, Chapter 1: "The Skew Field of Quaternions" (23 pages) ISBN 978-0-8218-4495-3.
- Vince, John A. (2008), Geometric Algebra for Computer Graphics, Springer, ISBN 978-1-84628-996-5.
- For molecules that can be regarded as classical rigid bodies molecular dynamics computer simulation employs quaternions. They were first introduced for this purpose by D.J. Evans, (1977), "On the Representation of Orientation Space", Mol. Phys., vol 34, p 317.
وصلات خارجية
- Matrix and Quaternion FAQ v1.21 Frequently Asked Questions
- "Geometric Tools documentation" (frame; body) includes several papers focusing on computer graphics applications of quaternions. Covers useful techniques such as spherical linear interpolation.
- Patrick-Gilles Maillot Provides free Fortran and C source code for manipulating quaternions and rotations / position in space. Also includes mathematical background on quaternions.
- "Geometric Tools source code" (frame; body) includes free C++ source code for a complete quaternion class suitable for computer graphics work, under a very liberal license.
- Doug Sweetser, Doing Physics with Quaternions
- Quaternions for Computer Graphics and Mechanics (Gernot Hoffman)
- The Physical Heritage of Sir W. R. Hamilton (PDF)
- D. R. Wilkins, Hamilton’s Research on Quaternions
- Quaternion Julia Fractals 3D Raytraced Quaternion Julia Fractals by David J. Grossman
- Quaternion Math and Conversions Great page explaining basic math with links to straight forward rotation conversion formulae.
- John H. Mathews, Bibliography for Quaternions.
- Quaternion powers on GameDev.net
- Andrew Hanson, Visualizing Quaternions home page.
- Representing Attitude with Euler Angles and Quaternions: A Reference, Technical report and Matlab toolbox summarizing all common attitude representations, with detailed equations and discussion on features of various methods.[dead link]
- Charles F. F. Karney, Quaternions in molecular modeling, J. Mol. Graph. Mod. 25(5), 595-604 (Jan. 2007); DOI: 10.1016/j.jmgm.2006.04.002; E-print arxiv:0506177.
- Johan E. Mebius, A matrix-based proof of the quaternion representation theorem for four-dimensional rotations., arXiv General Mathematics 2005.
- Johan E. Mebius, Derivation of the Euler-Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations., arXiv General Mathematics 2007.
- NUI Maynooth Department of Mathematics, Hamilton Walk.
- OpenGL:Tutorials:Using Quaternions to represent rotation
- David Erickson, Defence Research and Development Canada (DRDC), Complete derivation of rotation matrix from unitary quaternion representation in DRDC TR 2005-228 paper.[3]
- Alberto Martinez, University of Texas Department of History, "Negative Math, How Mathematical Rules Can Be Positively Bent",[4]
- D. Stahlke, Quaternions in Classical Mechanics[5]
- Morier-Genoud, Sophie, and Valentin Ovsienko. "Well, Papa, can you multiply triplets?",[6] describes how the quaternions can be made into a skew-commutative algebra graded by Z/2×Z/2×Z/2.
الهامش
برامج
- Quaternion Calculator [Java], theworld.com
- Quaternion Toolbox for Matlab, qtfm.sourceforge.net
- Boost library support for Quaternions in C++, boost.org
- Mathematics of flight simulation >Turbo-PASCAL software for quaternions, Euler angles and Extended Euler angles, xs4all.nl