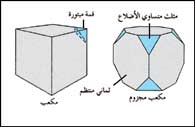
مجسم أرخميدي
المجسم الأرخميدي أحد ثلاثة عشر شكلاً مجسمًا، لها خواص متميزة. وصف المجسمات الأرخميدية في البداية الرياضي اليوناني القديم أرخميدس. والمجسمات الأرخميدية متعددات سطوح شبه منتظمة ومحدبة. وتمثّل سطوح أيّ مجسم أرخميدي أكثر من نوع واحد من المضلع المنتظم. ولكن كل الزوايا المجسمة متطابقة. وتتكون الزاوية المجسمة عند رأس (نقطة) التقاء ثلاثة وجوه أو أكثر.
وأحد أمثلة المجسمات الأرخميدية المكعّب المجزوم. وهذا الشكل يتكوّن عندما يجزم (يبتر) كل ركن من أركان المربع بنفس الزاوية، مما يؤدي إلى إحلال مثلث متساوي الأضلاع محل كل ركن. ويؤدي هذا بدوره إلى إحلال ثماني منتظم محل كل وجه مربّع من المكعب. وهكذا، فإن المكعب المجْزوم له ستّة وجوه من الثمانيات المنتظمة وثمانية وجوه من المثلثات المتساوية الأضلاع. وكل قمّة ركن لمثلث واحد أو ثمانيين.
التصنيف
There are 13 Archimedean solids (15 if the mirror images of two enantiomorphs, see below, are counted separately). Here the vertex configuration refers to the type of regular polygons that meet at any given vertex. For example, a vertex configuration of (4,6,8) means that a square, hexagon, and octagon meet at a vertex (with the order taken to be clockwise around the vertex).
The number of vertices is 720° divided by the vertex angle defect.
| Name (Vertex configuration) |
الشفاف | المجسم | Net | الأوجه | الحواف | الرؤوس | مجموعة التماثل | |
|---|---|---|---|---|---|---|---|---|
| truncated tetrahedron (3.6.6) |
 (Animation) |

|

|
8 | 4 triangles 4 hexagons |
18 | 12 | Td |
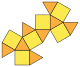
| cuboctahedron (3.4.3.4) |
 (Animation) |

|
|
14 | 8 triangles 6 squares |
24 | 12 | Oh |
| truncated cube or truncated hexahedron (3.8.8) |
 (Animation) |

|

|
14 | 8 مثلثات 6 مثمنات |
36 | 24 | Oh |
| truncated octahedron (4.6.6) |
 |

|

|
14 | 6 مربعات 8 مسدسات |
36 | 24 | Oh |
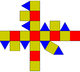
| rhombicuboctahedron or small rhombicuboctahedron (3.4.4.4 ) |
 (Animation) |

|
|
26 | 8 مثلثات 18 مربعات |
48 | 24 | Oh |
| truncated cuboctahedron or great rhombicuboctahedron (4.6.8) |
 (Animation) |

|

|
26 | 12 squares 8 مسدسات 6 مثمنات |
72 | 48 | Oh |
| snub cube or snub hexahedron or snub cuboctahedron (2 chiral forms) (3.3.3.3.4) |
 (Animation)  (Animation) |

|

|
38 | 32 مثلثات 6 مربعات |
60 | 24 | O |
| icosidodecahedron (3.5.3.5) |
 (Animation) |

|

|
32 | 20 triangles 12 pentagons |
60 | 30 | Ih |
| truncated dodecahedron (3.10.10) |
 (Animation) |

|

|
32 | 20 triangles 12 decagons |
90 | 60 | Ih |
| truncated icosahedron or buckyball or football/soccer ball (5.6.6 ) |
 (Animation) |

|

|
32 | 12 pentagons 20 hexagons |
90 | 60 | Ih |
| rhombicosidodecahedron or small rhombicosidodecahedron (3.4.5.4) |
 (Animation) |

|

|
62 | 20 مثلثات 30 مربعات 12 مخمسات |
120 | 60 | Ih |
| truncated icosidodecahedron or great rhombicosidodecahedron (4.6.10) |
 (Animation) |

|

|
62 | 30 مربعات 20 مسدسات 12 معشرات |
180 | 120 | Ih |
| snub dodecahedron or snub icosidodecahedron (2 chiral forms) (3.3.3.3.5) |
 (Animation)  (Animation) |

|

|
92 | 80 مثلثات 12 مخمسات |
150 | 60 | I |
انظر أيضاً
المصادر
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
وصلات خارجية
- Eric W. Weisstein, Archimedean solid at MathWorld.
- Archemedian Solids by Eric W. Weisstein, Wolfram Demonstrations Project.
- Paper models of Archimedean Solids and Catalan Solids
- Paper models(nets) of Archimedean solids
- The Uniform Polyhedra by Dr. R. Mäder
- Virtual Reality Polyhedra, The Encyclopedia of Polyhedra by George W. Hart
- Penultimate Modular Origami by James S. Plank
- Interactive 3D polyhedra in Java
- Contemporary Archimedean Solid Surfaces Designed by Tom Barber
- Stella: Polyhedron Navigator: Software used to create many of the images on this page.