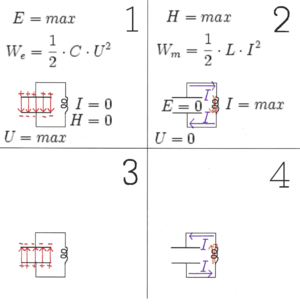دائرة رنان توافقي

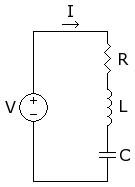
الرنان التوافقي أو دائرة الرنان بالإنجليزية Resonant Circuit أو RLC circuit هي دائرة كهربية مكونة من مقاومة و ملف و مكثف موصلين على التوالي أو التوازي ويشكلون معا رنانا توافقيا ، أي أن تلك الدائرة إما أن تكون مرسلا للإشارات أو مستقبلا للموجات الكهرطيسية عندما تُضبط لاستقبال موجة المرسل.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 وصف الرنان

تحتوي دائرة الرنان دائما على مقاومة تشكل الطاقة المفقودة في أسلاك التوصيل والملف والمكثف وهي طاقة الموجات الكهرومغناطيسية المنبثة من الدائرة . ويتميز التيار الكهربائي I_R بأنه يتردد بنفس طور الجهدU والذي تكون له أيضا قيمة فوق الصفر في حالة الرنين . ولذلك فلن تصل قيمة المقاومة في حالة الرنين للتوصيلة على التوازي إلى مالا نهاية . إلا أن المقاونة التخيلية (المركبة) Z قد تصل إلى نهاية عظمى :

وبصفة عامة تكون الطاقة المفقودة من المكثف أقل بكثير من الطاقة المفقودة (أو المرسلة) من الملف . وتُشكل مقاومة الملف عادة بتوصيل L_p و R_p على التوالي . ويمكن تعديل تلك التوصيلة إلى نظيرتها الموصولة على التوازي حيث نحصل على الصورة اليمنى . فتكون القيمة الناتجة عن توصيل المكثف C و الملف L_p مساويا للصفر في حالة الرنين . وهي هذه الحالة تقتصر الممانعة في دائرة التوصيل على التوازي على المقاومة R_p والتي تقاس بالأوم ، ونحصل على :

$Z_{\mathrm {r} }=R_{p\ \mathrm {r} }={\frac {L}{R_{L}C}}$

وينطبق تردد الرنين f₀ في الحالة المثالية عندما تكون R_L = 0. ولكن الدائرة الواقعية التي نتعامل معها هنا لها مقاومة أكبر من الصفر :

$f_{\mathrm {r} }={\frac {1}{2\pi {\sqrt {L_{p}C}}}}$

وهذه أصغر قليلا من $f_{0}$ ويمكن حسابها :

$f_{\mathrm {r} }={\frac {1}{2\pi }}{\sqrt {{\frac {1}{LC}}-{\frac {{R_{L}}^{2}}{L^{2}}}}}=f_{0}{\sqrt {1-{\frac {R_{L}}{Z_{\mathrm {r} }}}}}$

 كيف يحدث الرنين

طاقة كهربية E ، التيار I ، طاقة مغنايسية (مشحونة) H ، الجهد U.

في دائرة التوصيل على التوازي:

1. نعتبر أولا لحظة أن يكون المكثف بكامل شحنته . عندئذ يكون الجهد أعلى ما يكون على قطبي المكثف وبالتالي على دائرة الرنان (شكل 1).
2. يتسبب الجهد الموجود في مرور تيار ويبدأ المكثف يفقد شحنته أولا بسرعة ثم ببطء . ويحدث ذلك لأن تزايد مرور التيار في الملف ينتج جهدا في الملف مضادا بسبب الحث ، مما يهدئ من مرور التيار .
3. ويقل الجهد حتي يختفي في هذا الوقت تصل شدة التيار نهايتها العظمى . وفي هذا الوقت أيضا تكون شدة المجال المغناطيسي في الملف نهايته العظمي ويفقد المكثف كل شحنته . وتكون الطاقة الآن مشحونة في المجال المغناطيسي للملف (شكل 2) .
4. بعدما وصلت شدة التيار أقصاها تبدأ في الانهيار ثانيا ويقل بالتالي المجال المغناطيسي في الملف . وطبقا لقاعدة لنز يتسبب ذلك في نشأة جهد بالحث ويكون ذو إتجاه مضاد ، بحيث تنهار شدة التيار ببطء شديد. وبالتالي يرتفع فرق الجهد بين لوحي المكثف ثانيا إلا أنه يكون معكوس القطبية بالنسبة للحالة الأولى . وهذا ينطبق أيضا على الجهد في دائرة الرنان حيث يتزايد هذا الجهد بقطبية معكوسة .
5. بينما تنخفض شدة التيار ثانيا حتي تصل إلى الصفر ، يحصل المكثف على شحنته الأصلية ثانيا . وتتحول طاقة المجال المغناطيسي المخزونة عدة مرات إلى تيار كهربائي (شكل 3).
6. ثم تعيد تلك العوامل نفسها في اتجاه مضاد .

  توهين الذبذبة

توهين الذبذبة أو إضعاف مطال الموجة α للرنان الموصل على التوالي ، يعرف بالعلاقة الآتية:

$\alpha ={R \over 2L}$

ويعرف للرنان RLC الموصل على التوازي بالعلاقة:

$\alpha ={1 \over 2RC}$

 معامل التخميد

يعرف معامل التخميد damping factor ζ بأنه النسبة بين التهوين α وتردد الرنين ω₀:

وعلى ذلك فمعامل التخميد لرنان RLC الموصل على التوالي ، يبلغ :

$\zeta ={\alpha \over \omega _{0}}={R \over 2}{\sqrt {C \over L}}$

كما يبلغ في حالة الرنان الموصّل على التوازي :

$\zeta ={\alpha \over \omega _{0}}={1 \over 2R}{\sqrt {L \over C}}$

ويسهل من الوجهة العملية التعامل مع معامل التخميد ζ عن التعامل مع معامل التهوين α حيث أن معامل التخميد كمية مطلقة (بدون وحدات) في حين أن معامل التهوين يًقاس بوحدة راديان/ثانية ، عند دراسة خواص الرنان .

والعلاقة بين التردد الزاوي والتردد بالهرتز هي:

$f_{0}={\omega _{0} \over 2\pi }$

ويقاس التردد أو الذبذبة f بالهرتز أو بالكيلو هرتز.

 عرض المحزم

عرض المحزم ويحدده النقطتين التي ينخفص عندهما الجهد الكهربى إلى 0.707 من نهايته العظمى من مطال الاستجابة.

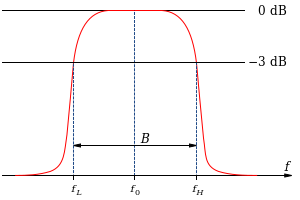
تستعمل دائرة الرنين أحيانا كمرشح للتردد حيث تسمح للترددات بالمرور في حيز ضيق وتمنع الترددات الأخرى من المرور . ويسمى هذا الحيز الضيق للترددات عرض المحزم وكلمة محزم تأتي من كلمة حزمة . ولتشفيل الدائرة كمرشح نستبدل المقاومة R بجهاز استقبال ويكون له نفس قيمة المقاومة R. ويصبح حيز المحزم للدائرة الموصولة غلى التوالي محددا بالعلاقة الآتية (بوحدة راديان/ثانية):

$\Delta \omega =2\alpha =2\zeta \omega _{0}={R \over L}$

ويمكن حساب عرض المحزم بوحدة هرتز بالعلاقة:

$\Delta f={\Delta \omega \over 2\pi }={\alpha \over \pi }={\zeta \omega _{0} \over \pi }={R \over 2\pi L}$

ويحدد عرض المحزم حزمة الترددات التي يُسمح لها بالمرور عند تردد نصف القدرة . وهو مقياس ينتسب إلى مطال الجهد الكهربي في منطقة عرض المحزم . وبما أن القدرة تتناسب تناسبا طرديا مع مربع الجهد ، فإن عرض المحزم يحدد من جهتيه عند النقطتين التي تنخفض استجابة التردد عندهما إلى ${1 \over {\sqrt {2}}}$ من تردد الرنين .

 حساب تردد الرنين

نفترض المكونات الآتية لدائرة الرنان الموصول على التوالي:

C = 0,1 μF; L = 50 μH; R_L = 5 Ω

حيث : سعة المكثف (ميكرو فاراد) ; و حث الملف (ميكرو هنري) ; و المقاومة أوم.

بالتعويض عن تلك القيم في معادلة تردد الرنين :

$f_{\mathrm {r} }={\frac {1}{2\pi {\sqrt {L_{p}C}}}}$

نحصل على :

10⁶ $f_{\mathrm {r} }={\frac {1}{2\pi {\sqrt {50*0,1}}}}$

$f_{\mathrm {r} }=69kHerz$

 اقرأ أيضا

• مرشح
• دائرة مقاومة و مكثف
• دائرة مقاومة و ملف
• توليف (راديو).
• تخميد
• عرض محزم