دائرة مقاومة و مكثف

دائرة مقاومة ومكثف ، بالإنجليزية Resistor-capacitor circuit أو (RC Circuit) أو (RC Filter) هي دائرة كهربية تحتوي على مقاومات و مكثفات وتعمل بالتيار المتردد . أبسط أنواع تلك الدوائر تحتوي على مقاومة واحدة ومكثف واحد . تستعمل كثيرا في الدوائر الكهربائية و الإلكترونيات كمرشح . وتبين الصورة ثلاثة مقاومات مختلفة ، وتدل مجموعة الحلقات الملونة المرسومة عليها على قيمتها بالأوم.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

مقدمة

توجد أساسا ثلاثة أنواع من الأجزاء التي تعمل كامنة وخطية في الدوائر الكهربية : المقاومة (R) و المكثف (C) و المستحث (L). ويمكن أن توصل هذه المكونات في تشكيلات : دائرة مقاومة ومكثف RC circuitو دائرة مقاومة ومستحث RL circuit و دائرة مستحث ومكثف LC circuit أو دائرة مقاومة ومستحث ومكثف RLC circuit. وتتبوء تلك الأنواع من الدوائر الكهربية مركزا مهما في الإلكترونيات التناظرية analog electronics. وهي تعمل على الأخص كمرشحات كامنة . هذه المقالة تتعلق بنوع دائرة المقاومة ومكثف . تعتمد تلك المقالة على معرفة سابقة بالخواص المركبة لمكونات تلك الدوائر ، ومعرفة بالتيار الكهربائي المتردد وتمثيل الإشارات.

المعاوقة المركبة

تزيد المقاومة المكافئة لمكثف بزيادة الشحنة الكهربية المخزونة فيه .فإذا وصل المكثف بمصدر جهد متردد alternating current ، فإن شحنة المكثف تتأرجح بنفس تردد جهد المصدر المتردد . وكلما زاد تردد الجهد كلما تجمعت شحنة أصغر على المكثف بسبب قصر زمن الطور ، وبذلك تقل المقاومة المكافئة للمكثف . وهذا ما يفسر العلاقة العكسية بين المقاومة المكافئة للمكثف وتردد جهد المصدر .

المقاومة والمسماة المعاوقة المركبة Z_C بالأوم لمكثف ذو سعة C فاراد تساوي:

Z_{C}={\frac {1}{sC}}

ويكون التردد الزاوي s عددا مركبا:

s\ =\ \sigma +j\omega

حيث :

j تمثل الجزء التخيلي :

j^{2}=-1

$\sigma \$ ثابت التحلل للدالة الأسية للأساس e بالراديان /ثانية ،

$\omega \$ التردد الزاوي الجيبي sinusoidal angular frequency بوحدة راديان/ثانية.

دائرة التوصيل على التوالي

Series RC circuit

باعتبار الدائرة موزع للجهد ، نجد أن الجهد عبر المكثف يساوي:

V_{C}(s)={\frac {1/Cs}{R+1/Cs}}V_{in}(s)={\frac {1}{1+RCs}}V_{in}(s)

كما نجد الجهد عبر المقاومة :

V_{R}(s)={\frac {R}{R+1/Cs}}V_{in}(s)={\frac {RCs}{1+RCs}}V_{in}(s)

.

ويكون التيار متساويا عبر الدائرة كلها حيث أنها موصّلة على التوالي:

I(s)={\frac {V_{in}(s)}{R+1/Cs}}={Cs \over 1+RCs}V_{in}(s)

الاستجابة للإشارة

تمثل استجابة الدائرة للجهد الموصل بها في هيئة إشارة كهربية ، استجابة المكثف والمقاومة .

استجابة المكثف للإشارة:

h_{C}(t)={1 \over RC}e^{-t/RC}u(t)={1 \over \tau }e^{-t/\tau }u(t)

\tau \ =\ RC

ثابت زمني يعتمد على سعة المكثف ومقدار المقاومة .

ويُعطى ستجابة المقاومة للإشارة الكهربية :

h_{R}(t)=\delta (t)-{1 \over RC}e^{-t/RC}u(t)=\delta (t)-{1 \over \tau }e^{-t/\tau }u(t)

حيث تسمى δ(t) دالة دلتا لديراك .

الثابت الزمني $\tau$ يحدد سرعة انهيار شحنة المكثف أو سرعة شحنه ويمكن التحكم في تلك السرعة بتغيير قيمة المقاومة أو سعة المكثف أو كلاهما معا .

تغير شحنة المكثف مع الزمن

نفترض أن جهد الإشارة الداخلة:

$V_{in}=0$ عند الزمن $t=0$

ثم تتغير وتصبح

V_{in}=V

:

V_{in}(s)=V{\frac {1}{s}}

أي أن Vin تتغير بتغير التردد الزاوي s (أنظر أعلاه)،

V_{C}(s)=V{\frac {1}{1+sRC}}{\frac {1}{s}}

وتكون:

V_{R}(s)=V{\frac {sRC}{1+sRC}}{\frac {1}{s}}

.

تزايد جهد المكثف مع الزمن.

تناقص جهد المقاومة مع الزمن .

وبتحليل تلك العلاقات نحصل على :

\,\!V_{C}(t)=V\left(1-e^{-t/RC}\right)

\,\!V_{R}(t)=Ve^{-t/RC}

.

تساعدنا تلك المعادلات على حساب الجهد عبر المكثف والمقاومة في وقت زيادة شحنة المكثف . وعند تفريغ المكثف ينعكس تغير المعادلات مع الزمن t. ويمكننا حساب الشحنة وتغيرها مع الزمن C=Q/V كما يمكننا حساب التيار وتغيره مع الزمن V=IR طبقا لقانون أوم.

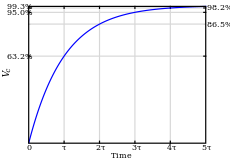
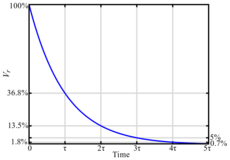
يميل جهد المكثف لاتخاذ القيمة V بمرور الزمن ، بينما يتجه جهد المقاومة نحو الصفر كما يبين المنحنيان . ويمكننا فهم ذلك أن المكثف تكتمل شحنته رويدا رويدا حتى تكتمل شحنته، عندئذ يقف التيار وتصبح الدائر مفتوحة.

تبين تلك المعادلات أن دائرة المقاومة ومكثف تتميز بثابت زمني يرمز له< math>\tau = RC</math> وهو الوقت الذي يزيد فيه الجهد عبر المكثف أوينخفض عبر المقاومة بنسبة $1/e$ من قيمته النهائية . أي أن $\tau$ هو الوقت اللازم لكي تصل $V_{C}$ إلى القيمة $V(1-1/e)$ ، و جهد المقاومة $V_{R}$ لكي يصل إلى القيمة $V(1/e)$ .

ومعدل تغير الشحنة هو نسبة $\left(1-{\frac {1}{e}}\right)$ إلى $\tau$ . وعلى ذلك عند تغير $t=N\tau$ إلى $t=(N+1)\tau$ يكون الجهد قد تغير بنسبة 63.2 % من قيمته النهائية $t=N\tau$ . أي أن المكثف يكون قد وصل إلى 63.2 % من شحنته بعد زمن $\tau$ ويصل إلى 99.3 % من شحنته النهائية بعد $5\tau$ . وعندما تُغلق الدائرة ويكون المكثف مشحونا تماما ينخفض الجهد عبر C طبقا للدالة الأسية e بالأس t من $V$ إلى 0. وتتفرغ شحنة C إلى 36.8 % (=1/e) بعد مرور $\tau$ وتقترب من التفريغ بنسبة 0.7 % بعد زمن $5\tau$ .