مطال

المطال Amplitude، هو السعة القصوى من متذبذبة، أو موجة، خلال تغير دوري في الفيزياء. ففي حالة البندول، يتأرجح البندول من مقدار إزاحة عظمى (مطال) عائدا إلى نقطة الاتزان ومنها إلى إزاحة عظمى على الناحية الأخرى ثم يعود في إتجاه نقطة الاتزان، وهكذا. والمطال هي مقدار الإزاحة العظمى.

وتتسم الحركة الموجية بالتغير الدوري ، وتقاس طول الموجة ${\mathcal {}}\lambda$ بالمسافة بين مطالين متتاليين عند مساواة طــَوْرهما في السـّياق. وكما نري في الرسم توضيحي الذي يبين الموجة الضوئية المكونة من مجال كهربائي متردد ، قيمة مطاله ${\mathcal {}}E$ ، ومتعامد عليه مجال مغناطيسي متردد ، قيمة مطاله المغناطيسي ${\mathcal {}}M$ .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

المفاهيم

A sinusoidal curve
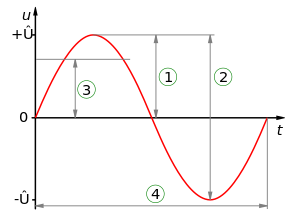
1 = Peak amplitude (

\scriptstyle {\hat {U}}

),
2 = Peak-to-peak amplitude (

\scriptstyle 2{\hat {U}}

),
3 = RMS amplitude (

\scriptstyle {\hat {U}}/{\sqrt {2}}

),
4 = Wave period (not an amplitude)

التمثيل الرسمي

في المعادلة الموجية المبسطة:

x=A\sin(t-K)+b\ ,

A is the peak amplitude of the wave,
x is the oscillating variable,
t is time,
K and b are arbitrary constants representing time and displacement offsets respectively.

Waveform and envelope

For a sine wave the relationship between RMS and peak-to-peak amplitude is:

{\mbox{Peak-to-peak}}=2{\sqrt {2}}\times {\mbox{RMS}}\approx 2.8\times {\mbox{RMS}}\,

.

For other waveforms the relationships are not (necessarily) arithmetically the same as they are for sine waves.

انظر أيضاً

هوامش