إثبات العمل

Proof of work (PoW) is a form of cryptographic zero-knowledge proof in which one party (the prover) proves to others (the verifiers) that a certain amount of a specific computational effort has been expended. Verifiers can subsequently confirm this expenditure with minimal effort on their part. The concept was invented by Cynthia Dwork and Moni Naor in 1993 as a way to deter denial-of-service attacks and other service abuses such as spam on a network by requiring some work from a service requester, usually meaning processing time by a computer. The term "proof of work" was first coined and formalized in a 1999 paper by Markus Jakobsson and Ari Juels.^[1]^[2] Proof of work was later popularized by Bitcoin as a foundation for consensus in permissionless decentralized network, in which miners compete to append blocks and mint new currency, each miner experiencing a success probability proportional to their computational effort expended. PoW and PoS (proof of stake) are the two best known Sybil deterrence mechanisms. In the context of cryptocurrencies they are the most common mechanisms.^[3]

A key feature of proof-of-work schemes is their asymmetry: the work – the computation – must be moderately hard (yet feasible) on the prover or requester side but easy to check for the verifier or service provider. This idea is also known as a CPU cost function, client puzzle, computational puzzle, or CPU pricing function. Another common feature are built-in incentive-structures that reward allocating computational capacity to the network with value in the form of money.

The purpose of proof-of-work algorithms is not proving that certain work was carried out or that a computational puzzle was "solved", but deterring manipulation of data by establishing large energy and hardware-control requirements to be able to do so.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Background

One popular system, used in Hashcash, uses partial hash inversions to prove that computation was done, as a goodwill token to send an e-mail. For instance, the following header represents about 2⁵² hash computations to send a message to calvin@comics.net on January 19, 2038:

X-Hashcash: 1:52:380119:calvin@comics.net:::9B760005E92F0DAE

It is verified with a single computation by checking that the SHA-1 hash of the stamp (omit the header name X-Hashcash: including the colon and any amount of whitespace following it up to the digit '1') begins with 52 binary zeros, that is 13 hexadecimal zeros:^[1]

0000000000000756af69e2ffbdb930261873cd71

Whether PoW systems can actually solve a particular denial-of-service issue such as the spam problem is subject to debate;^[4]^[5] the system must make sending spam emails obtrusively unproductive for the spammer, but should also not prevent legitimate users from sending their messages. In other words, a genuine user should not encounter any difficulties when sending an email, but an email spammer would have to expend a considerable amount of computing power to send out many emails at once. Proof-of-work systems are being used by other, more complex cryptographic systems such as bitcoin, which uses a system similar to Hashcash.^[4]

Variants

There are two classes of proof-of-work protocols.

Challenge–response protocols assume a direct interactive link between the requester (client) and the provider (server). The provider chooses a challenge, say an item in a set with a property, the requester finds the relevant response in the set, which is sent back and checked by the provider. As the challenge is chosen on the spot by the provider, its difficulty can be adapted to its current load. The work on the requester side may be bounded if the challenge-response protocol has a known solution (chosen by the provider), or is known to exist within a bounded search space.

Solution–verification protocols do not assume such a link: as a result, the problem must be self-imposed before a solution is sought by the requester, and the provider must check both the problem choice and the found solution. Most such schemes are unbounded probabilistic iterative procedures such as Hashcash.

Known-solution protocols tend to have slightly lower variance than unbounded probabilistic protocols because the variance of a rectangular distribution is lower than the variance of a Poisson distribution (with the same mean). A generic technique for reducing variance is to use multiple independent sub-challenges, as the average of multiple samples will have a lower variance.

There are also fixed-cost functions such as the time-lock puzzle.

Moreover, the underlying functions used by these schemes may be:

CPU-bound where the computation runs at the speed of the processor, which greatly varies in time, as well as from high-end server to low-end portable devices.^[6]
Memory-bound^[7]^[8]^[9]^[10] where the computation speed is bound by main memory accesses (either latency or bandwidth), the performance of which is expected to be less sensitive to hardware evolution.
Network-bound^[11] if the client must perform few computations, but must collect some tokens from remote servers before querying the final service provider. In this sense, the work is not actually performed by the requester, but it incurs delays anyway because of the latency to get the required tokens.

Finally, some PoW systems offer shortcut computations that allow participants who know a secret, typically a private key, to generate cheap PoWs. The rationale is that mailing-list holders may generate stamps for every recipient without incurring a high cost. Whether such a feature is desirable depends on the usage scenario.

List of proof-of-work functions

Here is a list of known proof-of-work functions:

Integer square root modulo a large prime^[2]Modular square roots^{[محل شك]}
Weaken Fiat–Shamir signatures^[2]
Ong–Schnorr–Shamir signature broken by Pollard^[2]
Partial hash inversion^[12]^[13]^[1] This paper formalizes the idea of a proof of work and introduces "the dependent idea of a bread pudding protocol", a "re-usable proof-of-work" (RPoW) system.^[14]
Hash sequences^[15]
Puzzles^[16]
Diffie-Hellman–based puzzle^[17]
Moderate^[7]
Mbound^[8]
Hokkaido^[9]
Cuckoo Cycle^[10]
Merkle tree–based^[18]
Guided tour puzzle protocol^[11]

Reusable proof-of-work

Computer scientist Hal Finney built on the proof-of-work idea, yielding a system that exploited reusable proof of work (RPoW).^[19] The idea of making proofs of work reusable for some practical purpose had already been established in 1999.^[1] Finney's purpose for RPoW was as token money. Just as a gold coin's value is thought to be underpinned by the value of the raw gold needed to make it, the value of an RPoW token is guaranteed by the value of the real-world resources required to 'mint' a PoW token. In Finney's version of RPoW, the PoW token is a piece of Hashcash.

A website can demand a PoW token in exchange for service. Requiring a PoW token from users would inhibit frivolous or excessive use of the service, sparing the service's underlying resources, such as bandwidth to the Internet, computation, disk space, electricity, and administrative overhead.

Finney's RPoW system differed from a PoW system in permitting the random exchange of tokens without repeating the work required to generate them. After someone had "spent" a PoW token at a website, the website's operator could exchange that "spent" PoW token for a new, unspent RPoW token, which could then be spent at some third-party website similarly equipped to accept RPoW tokens. This would save the resources otherwise needed to 'mint' a PoW token. The anti-counterfeit property of the RPoW token was guaranteed by remote attestation. The RPoW server that exchanges a used PoW or RPoW token for a new one of equal value uses remote attestation to allow any interested party to verify what software is running on the RPoW server. Since the source code for Finney's RPoW software was published (under a BSD-like license), any sufficiently knowledgeable programmer could, by inspecting the code, verify that the software (and, by extension, the RPoW server) never issued a new token except in exchange for a spent token of equal value.

Until 2009, Finney's system was the only RPoW system to have been implemented; it never saw economically significant use.

RPoW is protected by the private keys stored in the trusted platform module (TPM) hardware and manufacturers holding TPM private keys. Stealing a TPM manufacturer's key or obtaining the key by examining the TPM chip itself would subvert that assurance.

Bitcoin-type proof of work

In 2009, the Bitcoin network went online. Bitcoin is a proof-of-work digital currency that, like Finney's RPoW, is also based on the Hashcash PoW. But in Bitcoin, double-spend protection is provided by a decentralized P2P protocol for tracking transfers of coins, rather than the hardware trusted computing function used by RPoW. Bitcoin has better trustworthiness because it is protected by computation. Bitcoins are "mined" using the Hashcash proof-of-work function by individual miners and verified by the decentralized nodes in the P2P bitcoin network.

The difficulty is periodically adjusted to keep the block time around a target time.

Energy consumption

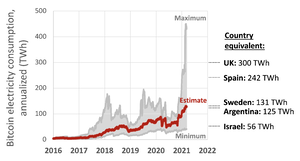
Bitcoin electricity consumption as of 2021^[20]

Since the creation of Bitcoin, proof-of-work has been the predominant design of peer-to-peer cryptocurrency. Studies have estimated the total energy consumption of cryptocurrency mining.^[21] The PoW mechanism requires a vast amount of computing resources, which consume a significant amount of electricity. Bitcoin's total energy consumption is equivalent to that of a small country.^[3] Bitcoin’s absolute electricity consumption and carbon emissions are not significant in global terms, representing 0.04 percent of global primary energy consumption, 0.2 percent of global electricity generation, and 0.1 percent of global carbon emissions.^[22] Bitcoin miners can reduce emissions in the short and medium term by buying carbon offsets, procuring renewable energy, favoring locations with renewable energy, and using wasted energy. In the long term, Bitcoin miners can benefit from grid decarbonization and likely advances in battery storage technology and the resulting lower storage costs.^[22]

History modification

Each block that is added to the blockchain, starting with the block containing a given transaction, is called a confirmation of that transaction. Ideally, merchants and services that receive payment in the cryptocurrency should wait for at least one confirmation to be distributed over the network, before assuming that the payment was done. The more confirmations that the merchant waits for, the more difficult it is for an attacker to successfully reverse the transaction in a blockchain—unless the attacker controls more than half the total network power, in which case it is called a 51% attack.^[23]

ASICs and mining pools

Within the Bitcoin community there are groups working together in mining pools.^[24] Some miners use application-specific integrated circuits (ASICs) for PoW.^[25] This trend toward mining pools and specialized ASICs has made mining some cryptocurrencies economically infeasible for most players without access to the latest ASICs, nearby sources of inexpensive energy, or other special advantages.^[26]

Some PoWs claim to be ASIC-resistant,^[27] i.e. to limit the efficiency gain that an ASIC can have over commodity hardware, like a GPU, to be well under an order of magnitude. ASIC resistance has the advantage of keeping mining economically feasible on commodity hardware, but also contributes to the corresponding risk that an attacker can briefly rent access to a large amount of unspecialized commodity processing power to launch a 51% attack against a cryptocurrency.^[28]