فئة محدبة

مجموعة محدبة.

مجموعة غير محدبة.

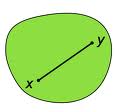
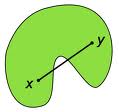
في الفضاء الإقليدي، نقول عن جسم أنه محدب Convex set إذا كانت القطعة المستقيمة الواصلة بين كل نقطتين من الجسم تقع بكاملها ضمن حدود الجسم.

على سبيل المثال، يعتبر المكعب محدباً، بينما شكل الهلال لا يعتبر محدباً.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انظر أيضاً

• دالة محدبة Convex function
• Holomorphically convex hull
• تحدب كاذب Pseudoconvexity
• Convex metric space
• فئة مقعرة
• مبرهنة هلي Helly's theorem
• Shapley–Folkman lemma