دالة هاش تشفيرية
.
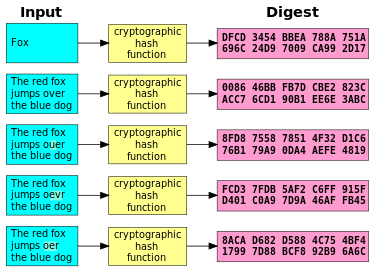
دالة هاش التشفيرية Cryptographic hash function، هي دالة هاش، بمعنى أنها تأخذ أي عدد من قطع البيانات وتعيد سلسلة ثابتة الطول من البتات تسمى قيمة هاش التشفيرية، بحيث أن أي تغيير في البيانات الاصلية (عرضياً أو متعمدا) سوف يؤدي إلى تغيير كبير في قيمة هاش التشفيرية (باحتمال كبير جداً). عادة تسمى البيانات المشفرة "الرسالة" ومقدار هاش التشفيري يسمى الخلاصة digest.
هذا النوع من الخوارزميات لا يحتاج إلى مفتاح تشفير لأنه لا يستخدم لتشفير النصوص وانما للتأكد من ان محتوى الرسالة موثوق ولم يتم التعديل عليه. وذلك بمقارنة الخلاصة المرسلة مع الخلاصة المولدة من الرسالة المطلوب التأكد من صحة محتواها.
من الأمثلة على دالة هاش التشفيرية خوارزميات إم دي5 وببر وSHA-1.
تمتلك دالة هاش التشفيرية المثالية اربع صفات اساسية:
- يمكن حساب خلاصة بسهولة لأي رسالة معطاة
- أنه من غير الممكن توليد رسالة انطلاقا من خلاصة معطاة
- أنه من غير الممكن تغيير رسالة من دون ان تتغير خلاصتها
- أنه من غير الممكن توليد رسالتين لهما نفس الخلاصة [1]
لدالات هاش التشفيرية تطبيقات عديدة في مجال أمن المعلومات، وخصوصاً في الامضاءات الرقمية، رموز استيقان الرسائل MAC، وأنواع الاستيقان الأخرى لاكتشاف المعلومات المكررة أو ملفات الكيانات [1]
الخصائص
تم نصميم اغلب دالات هاش التشفيرية لتأخذ سلسلة من المحارف من اي طول وتعيد قيمة هاش ثابتة الطول ان دالة هاش التشفيرية يجب ان تقاوم كل انواع هجوم تحليل التشفير المعروفة. وبالحد الأدنى يجب ان تتمتع بالخصائص التالية:
- مقاومة العكس او Preimage resistance
- بفرض قيمة هاش يجب ان يكون من الصعب ايجاد رسالة بحيث يكون .
يرتبط هذا المبدأ ب الدالات وحيدة الاتجاه او غير العكوسة. الدالات التي تفتقر لهذه الصفة تكون معرضة لهجوم العكس.
- مقاومة العكس الثاني او Second-preimage resistance
- بفرض وجود دخل او ورودي يجب ان يكون من الصعب ان نجد دخلا اخر حيث بحيث يكون .
يشار احيانا إلى هذه الخاصية بـِ مقاومة العكس الضعيف والدالات التي تفتقر لهذه الصفة تكون معرضة لهجوم العكس الثاني.
- مقاومة التصادم او Collision resistance
- يجب ان يكون من الصعب ايجاد رسالتين مختلفتين و بحيث يكون .
يطلق على زوج كهذا تصادم الهاش. يشار احيانا إلى هذه الخاصية بـِ مقاومة العكس القوي. يجب ان يكون طول قيمة الهاش على الاقل ضعف الطول المطلوب لمقاومة العكس, والا فستوجد التصادمات ب هجوم عيد الميلاد او Birthday attack.
تقتضي هذه الخصائص بأن العدو سيئ القصد لا يستطيع ان يستبدل او يغير بيانات الدخل بدون تغيير خلاصتها. وبالتالي, فاذا كان لدينا سلسلتين تملكان نفس الخلاصة, فانه يمكن الاطمئنان بانهما متطابقتان.[2]
الدالة التي تملك هذه الخصائص ربما تكون ما تزال تملك خصائص غير مستحبة. ان دالات الهاش التشفيرية الحالية معرضة لهجوم تمديد الطول: بفرض و ولكن ليس , باختيار مناسب يمكن للمهاجم ان يحسب بحيث تعني الوصل. يمكن استخدام هذه الخاصة لكسر طرق الاستيقان الاولية التي تعتمد على دالات الهاش. ان تركيب HMAC يتغلب على هذه المشاكل [3].
التطبيقات
التحقق من سلامة الرسائل والملفات
جيل التوقيع والتحقق
التحقق من كلمة السر
Proof-of-work
File or data identifier
Hash functions based on block ciphers
Hash function design
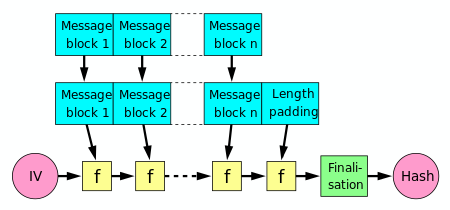
Merkle–Damgård construction
Wide pipe vs narrow pipe
Use in building other cryptographic primitives
Concatenation
Cryptographic hash algorithms
MD5
SHA-1
RIPEMD-160
bcrypt
Whirlpool
SHA-2
SHA-3
BLAKE2
Attacks on cryptographic hash algorithms
انظر أيضاً
|
|
المصادر
وصلات خارجية
- Paar, Christof; Pelzl, Jan (2009). "11: Hash Functions". Understanding Cryptography, A Textbook for Students and Practitioners. Springer. Archived from the original on 2012-12-08.
{{cite book}}: Unknown parameter|deadurl=ignored (|url-status=suggested) (help) (companion web site contains online cryptography course that covers hash functions) - "The ECRYPT Hash Function Website".
- Buldas, A. (2011). "Series of mini-lectures about cryptographic hash functions".
- (2004). "Cryptographic Hash-Function Basics: Definitions, Implications, and Separations for Preimage Resistance, Second-Preimage Resistance, and Collision Resistance".