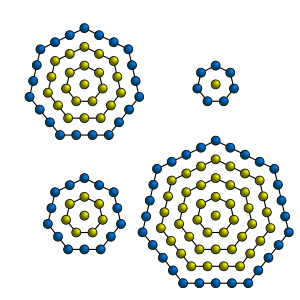
عدد ممركز مسبع

عدد ممركز مسبع.

العدد الممركز المسبع Centered heptagonal number هو عدد ممركز مضلع يتم تمثيله بمضلع سباعي الأضلاع منتظم. بحيث يكون هناك نقطة مركزية يحيط بها طبقات من نقاط تشكل سباعيات أضلاع. لهذا العدد الصيغة الرياضية التالية من أجل العدد n

${7n^{2}-7n+2} \over 2$.

ويمكن الحصول على هذه العلاقة بضرب عدد مثلثي من أجل (n - 1) بالرقم 7 ومن ثم إضافة 1.

وتعطى الأعداد الأولى من هذه السلسة على الشكل التالي: 1 - 8 - 22 - 43 - 71 - 106 - 148 - 197 - 253 - 316 - 386 - 463 - 547 - 638 - 736 - 841 - 953 - ...

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الأعداد الممركز السباعية الأولية

هي أعداد ممركزة سباعية أولية ويعطى بعضها كما يلي: 43 - 71 - 197 - 463 - 547 - 953 - 1471 - 1933 - ...

 انظر أيضاً

• Regular heptagonal number.