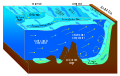
حيود ضغط الطبقات

خطوط الكثافة و خطوط تساوي الضغط تتقاطع في مائع باروكلينيكي (أعلى). فالكثافة ترتبط بدرجة الحرارة، على خريطة سطحية، نجد أن خطوط تساوي الضغط و خطوط تساوي درجات الحرارة تتقاطع هي الأخرى.

Visualization of a (fictive) formation of isotherms (red-orange) and isobars (blue) in a baroclinic atmospheric layering.

2:46

A rotating tank experiment modelling baroclinic eddies in the atmosphere

في ديناميكا الموائع، حيود ضغط الطبقات أو الباروكلينيكية baroclinity أو baroclinicity لمائع مكوّن من طبقات هو مقياس لحيود معدل تغير الضغط عن معدل تغير الكثافة في مائع. في علم الأرصاد الجوية فإن الغلاف الجوي الباروكلينيكي هو غلاف جوي تعتمد الكثافة فيه على كلٍ من درجة الحرارة والضغط؛ ويتباين ذلك مع الغلاف الجوي barotropic، الذي تعتمد الكثافة فيه فقط على الضغط. وفي سياق الغلاف الجوي، فإن المناطق barotropic من كوكب الأرض توجد عموماً في خطوط العرض الوسطى، أو المنطقة الإستوائية، بينما المناطق الباروكلينيكية توجد عموماً في مناطق بين خطوط العرض الوسطى والقطبية.

حيود ضغط الطبقات يتناسب طردياً مع

${\displaystyle{\displaystyle\nabla p\times\nabla\rho}}$

والذي يتناسب بدوره مع جيب الزاوية بين أسطح الضغط المتساوي وأسطح الكثافة المتساوية. وبذلك، ففي مائع barotropic (الذي يُعرَّف بـصِفر باروكلينيكية)، فإن تلك الأسطح تكون متوازية.

مناطق الحيود العالي لضغط طبقات الغلاف الجوي تتسم بتشكل متكرر للإعاصير.

In Earth's atmosphere, barotropic flow is a better approximation in the tropics, where density surfaces and pressure surfaces are both nearly level, whereas in higher latitudes the flow is more baroclinic. These midlatitude belts of high atmospheric baroclinity are characterized by the frequent formation of synoptic-scale cyclones, although these are not really dependent on the baroclinity term per se: for instance, they are commonly studied on pressure coordinate iso-surfaces where that term has no contribution to vorticity production.

 عدم الاستقرار بسبب حيود ضغط الطبقات

انظر أيضاً: Eady model

Baroclinic instability is a fluid dynamical instability of fundamental importance in the atmosphere and in the oceans. In the atmosphere it is the principal mechanism shaping the cyclones and anticyclones that dominate weather in mid-latitudes. In the ocean it generates a field of mesoscale eddies (100 km or smaller) that play various roles in oceanic dynamics and the transport of tracers.

Whether a fluid counts as rapidly rotating is determined in this context by the Rossby number, which is a measure of how close the flow is to solid body rotation. More precisely, a flow in solid body rotation has vorticity that is proportional to its angular velocity. The Rossby number is a measure of the departure of the vorticity from that of solid body rotation. The Rossby number must be small for the concept of baroclinic instability to be relevant. When the Rossby number is large, other kinds of instabilities, often referred to as inertial, become more relevant.

The simplest example of a stably stratified flow is an incompressible flow with density decreasing with height.

In a compressible gas such as the atmosphere, the relevant measure is the vertical gradient of the entropy, which must increase with height for the flow to be stably stratified.

The strength of the stratification is measured by asking how large the vertical shear of the horizontal winds has to be in order to destabilize the flow and produce the classic Kelvin–Helmholtz instability. This measure is called the Richardson number. When the Richardson number is large, the stratification is strong enough to prevent this shear instability.

Before the classic work of Jule Charney and Eric Eady on baroclinic instability in the late 1940s, most theories trying to explain the structure of mid-latitude eddies took as their starting points the high Rossby number or small Richardson number instabilities familiar to fluid dynamicists at that time. The most important feature of baroclinic instability is that it exists even in the situation of rapid rotation (small Rossby number) and strong stable stratification (large Richardson's number) typically observed in the atmosphere.

The energy source for baroclinic instability is the potential energy in the environmental flow. As the instability grows, the center of mass of the fluid is lowered. In growing waves in the atmosphere, cold air moving downwards and equatorwards displaces the warmer air moving polewards and upwards.

Baroclinic instability can be investigated in the laboratory using a rotating, fluid filled annulus. The annulus is heated at the outer wall and cooled at the inner wall, and the resulting fluid flows give rise to baroclinically unstable waves.

The term "baroclinic" refers to the mechanism by which vorticity is generated. Vorticity is the curl of the velocity field. In general, the evolution of vorticity can be broken into contributions from advection (as vortex tubes move with the flow), stretching and twisting (as vortex tubes are pulled or twisted by the flow) and baroclinic vorticity generation, which occurs whenever there is a density gradient along surfaces of constant pressure. Baroclinic flows can be contrasted with barotropic flows in which density and pressure surfaces coincide and there is no baroclinic generation of vorticity.

The study of the evolution of these baroclinic instabilities as they grow and then decay is a crucial part of developing theories for the fundamental characteristics of midlatitude weather.

 متجه حيود ضغط الطبقات

بدءاً بمعادلة الحركة لمائع عديم الاحتكاك (معادلات أويلر) وأخذ the curl, one arrives at the معادلة الحركة للـthe curl سرعة المائع، أي دوامية.

في مائع بلا كثافة ثابتة، a source term appears in the معادلة الدوامية whenever surfaces of constant density (isopycnic surfaces) and surfaces of constant pressure (isobaric surfaces) are not aligned. The material derivative of the local vorticity is given by

${\displaystyle{\displaystyle{\frac{D{\vec{\omega}}}{Dt}}\equiv{\frac{\partial{\vec{\omega}}}{\partial t}}+({\vec{u}}\cdot{\vec{\nabla}}){\vec{\omega}}=({\vec{\omega}}\cdot{\vec{\nabla}}){\vec{u}}-{\vec{\omega}}({\vec{\nabla}}\cdot{\vec{u}})+\underbrace{{\frac{1}{\rho^{2}}}{\vec{\nabla}}\rho\times{\vec{\nabla}}p}_{\text{baroclinic contribution}}}}$

(حيث ${\displaystyle{\displaystyle{\vec{u}}}}$ هو السرعة و ${\displaystyle{\displaystyle{\vec{\omega}}}}$ هو الدوامية، ${\displaystyle{\displaystyle p}}$ هو الضغط، و ${\displaystyle{\displaystyle\rho}}$ هو الكثافة). إسهام حيود ضغط الطبقات هو المتجه

${\displaystyle{\displaystyle{\frac{1}{\rho^{2}}}\nabla\rho\times\nabla p}}$

This vector, sometimes called the solenoidal vector, is of interest both in compressible fluids and in incompressible (but inhomogeneous) fluids. Internal gravity waves as well as unstable Rayleigh–Taylor modes can be analyzed from the perspective of the baroclinic vector. It is also of interest in the creation of vorticity by the passage of shocks through inhomogeneous media, كما في عدم استقرار ريشتماير-ميشكوڤ.