وقت شمسي

On a prograde planet like the Earth, the sidereal day is shorter than the solar day. At time 1, the Sun and a certain distant star are both overhead. At time 2, the planet has rotated 360° and the distant star is overhead again (1→2 = one sidereal day). But it is not until a little later, at time 3, that the Sun is overhead again (1→3 = one solar day). Or more simply, 1-2 is a complete rotation of the Earth, but because the revolution around the Sun affects the angle the Sun hits a position on the Earth, 1-3 is how long it takes noon to return

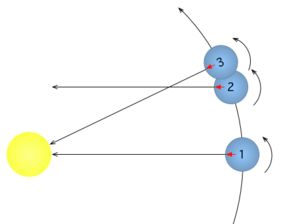
اليوم الشمسي هي الفترة من منتصف ليل واحد إلى آخر، اليوم الشمسي. يتغير طول اليوم الشمسي بسبب ميل محور الأرض، والشكل الإهليلجي ـ البيضاوي ـ لمدارها وتغير سرعتها عبر المدار. يمر خط وهمي منحن عبر السماء مباشرة فوق كل نقطة على الأرض، يدعى خط الزوال السماوي. وأثناء دوران الأرض حول محورها، تعبر الشمس خط الزوال السماوي هذا مرة كل يوم. وعند عبور الشمس هذا الخط فوق مكان معين يكون الوقت فيه ظهراً. وبعد 12 ساعة يصبح الوقت في ذلك المكان منتصف الليل.

ولجعل كل الأيام الشمسية بطول واحد، فإن الفلكيين لايقيسون التوقيت الشمسي بالشمس الظاهرة ـ الحقيقية ـ بل يستعملون عوضاً عن ذلك شمساً وسطية ـ خيالية ـ تتحرك بسرعة ثابتة حول السماء. يحدث الظهر الشمسي الوسطي المحلي عندما تَعبر الشمس الوسطية خط الزوال السماوي فوق مكان محدد ويكون الوقت بين ظهر شمسي وسطي واحد وبين الآخر هو دائماً ذاته. وهكذا فكل الأيام الشمسية الوسطية تكون بالطول نفسه.

طول اليوم الشمسي الظاهر (1998)

التاريخ	المدة في الوقت الشمسي المتوسط
11 فبراير	24 hours
March 26	24 hours − 18.1 seconds
May 14	24 hours
June 19	24 hours + 13.1 seconds
July 26	24 hours
16 سبتمبر	24 hours − 21.3 seconds
3 نوفمبر	24 hours
22 ديسمبر	24 hours + 29.9 seconds

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 المصادر

الموسوعة المعرفية الشاملة

 انظر أيضاً

• Local mean time
• Meridian circle
• Earth rotation
• Synodic day

 وصلات خارجية

• Sunrise and Sunset and maximum Sun altitude, all year long, anywhere
• Astrarium Solar Tempometer: Apparent solar time in a digital display.