مشكلة الأجسام الثلاث

هذا المقال هو عن النظرية الفيزيائية والميكانيكية الكلاسيكية. إذا كنت تريد رواية الخيال العلمي الصينية من تأليف ليو تسي‌شين، انظر مشكلة الأجسام الثلاث (رواية). إذا كنت تريد استخدامات أخرى، انظر مشكلة الأجسام الثلاث (توضيح).

مسارات تقريبية لثلاث هيئات متطابقة موجودة عند رؤوس مثلث مختلف الأضلاع ولا تملك سرعات أولية. يلاحظ أن مركز الكتلة, وفقاً لـ قانون حفظ الزخم، مازال قائما.

في الفيزياء والميكانيكا الكلاسيكية، مشكلة الأجسام الثلاث three-body problem، هي مشكلة أخذ مواضع ثلاث كتل و سرعتهم (أو كمية الحركة) لإيجاد حركتهم في وقت لاحق وفقا لقوانين الحركة لنيوتن و قانون نيوتن للجذب العام. مشكلة الأجسام الثلاث هي أحد حالات مشكلة الأجسام ن الخاصة، وعلى عكس مسألة الجسمين لا يوجد حل منغلق الشكل عام , فأدى ذلك إلى تحول النظام االتحريكي إلى فوضى بالنسبة لمعظم الشروط الأولى، وأصبحت الطرق العددية مطلوبة بشكل عام. تاريخيا، أول مشكلة أجسام ثلاث يتم دراستها بشكل موسع كانت مشكلة تتضمنت القمر و الأرض و الشمس. في مفهوم حديث وأكثر شمولاً، مشكلة ثلاثة أجسام هي أي مسالة في الميكانيكا الكلاسيكية أو ميكانيكا الكم تشكل نموذجاً رياضياً لوصف حركة ثلاثة جسيمات.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الوصف الرياضي

${\begin{aligned}{\ddot {\mathbf {r} }}_{\mathbf {1} }&=-Gm_{2}{\frac {\mathbf {r_{1}} -\mathbf {r_{2}} }{|\mathbf {r_{1}} -\mathbf {r_{2}} |^{3}}}-Gm_{3}{\frac {\mathbf {r_{1}} -\mathbf {r_{3}} }{|\mathbf {r_{1}} -\mathbf {r_{3}} |^{3}}},\\{\ddot {\mathbf {r} }}_{\mathbf {2} }&=-Gm_{3}{\frac {\mathbf {r_{2}} -\mathbf {r_{3}} }{|\mathbf {r_{2}} -\mathbf {r_{3}} |^{3}}}-Gm_{1}{\frac {\mathbf {r_{2}} -\mathbf {r_{1}} }{|\mathbf {r_{2}} -\mathbf {r_{1}} |^{3}}},\\{\ddot {\mathbf {r} }}_{\mathbf {3} }&=-Gm_{1}{\frac {\mathbf {r_{3}} -\mathbf {r_{1}} }{|\mathbf {r_{3}} -\mathbf {r_{1}} |^{3}}}-Gm_{2}{\frac {\mathbf {r_{3}} -\mathbf {r_{2}} }{|\mathbf {r_{3}} -\mathbf {r_{2}} |^{3}}}.\end{aligned}}$

${\frac {d\mathbf {r_{i}} }{dt}}={\frac {\partial {\mathcal {H}}}{\partial \mathbf {p_{i}} }},\qquad {\frac {d\mathbf {p_{i}} }{dt}}=-{\frac {\partial {\mathcal {H}}}{\partial \mathbf {r_{i}} }},$

حيث يكون ${\mathcal {H}}$ هو الهاميلتوني:

${\mathcal {H}}=-{\frac {Gm_{1}m_{2}}{|\mathbf {r_{1}} -\mathbf {r_{2}} |}}-{\frac {Gm_{2}m_{3}}{|\mathbf {r_{3}} -\mathbf {r_{2}} |}}-{\frac {Gm_{3}m_{1}}{|\mathbf {r_{3}} -\mathbf {r_{1}} |}}+{\frac {\mathbf {p_{1}} ^{2}}{2m_{1}}}+{\frac {\mathbf {p_{2}} ^{2}}{2m_{2}}}+{\frac {\mathbf {p_{3}} ^{2}}{2m_{3}}}.$

حيث يكون ${\mathcal {H}}$ ببساطة إجمالي طاقة النظام, الجاذبة زائد الحركية.

 مشكلة الأجسام الثلاث المقيدة

مشكلة ثلاث جسد دائرية مقيدة هي تقدير تقريبي صحيح لمدارات إهليلجية موجودة في النظام الشمسي, ويمكن تصور تلك المجموعة من الاحتمالات نتيجة للجسمين الأولين مع تأثير الطرد المركزي النابع من دورانهم تأثير كوريوليس على أنها غير مرئية ومن ثم يمكن النظر إلى نقاط لاگرنچ على أنها الخمسة نقاط التي يكون فيها الانحدار على السطح الناتج صفرًا (تلك النقاط الزرقاء)، مشيرة إلى أن القوى متوازنة هناك.

${\begin{aligned}{\frac {d^{2}x}{dt^{2}}}=-m_{1}{\frac {x-x_{1}}{r_{1}^{3}}}-m_{2}{\frac {x-x_{2}}{r_{2}^{3}}}\\{\frac {d^{2}y}{dt^{2}}}=-m_{1}{\frac {y-y_{1}}{r_{1}^{3}}}-m_{2}{\frac {y-y_{2}}{r_{2}^{3}}},\end{aligned}}$

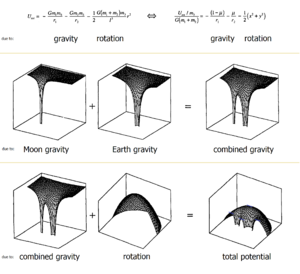
حيث أن $r_{i}={\sqrt {(x-x_{i})^{2}+(y-y_{i})^{2}}}$. في هذه الصيغة تحمل معادلات الحركة اعتماد واضح على الوقت من خلال النظيرين $x_{i}(t),y_{i}(t)$. ولكن من الممكن إزالة هذا الاعتماد الزمني من خلال التحول إلى إطار مرجعي دوار,مما يبسط أي تحليل لاحق.

 الحلول

 الحل العام

ولا يوجد حل تحليلي عام لمعضلة الأجسام الثلاث يتم إعطاؤه بواسطة التراكيب الجبرية البسيطة والكاملات. Moreover, وعلاوة على ذلك فأن حركة الأجسام الثلاث تكون غير متكررة إلا في حالات خاصة.

 حلول الحالة الخاصة

رسم متحرك لحل الشكل 8 لمشكلة الأجسام الثلاث على مدى فترة واحدة T ≃ 6.3259.

 التاريخ

 علم الفلك

كويكبات طروادة ونقاط لاگرنچ.

في كوكب المشترى، حيث العواصف التي تمتد لفترات زمنية كبيرة وحقل جاذبية كبير يجذب الأجسام الصغيرة التي يمكن أن تهدد الحياة على الأرض، هناك تكتلين في نفس مدار المشتري حول الشمس، أحدهما على يمينه والأخرى على يساره كما في الشكل أعلاه. هذا التكتل يحتوي على آلاف الكويكبات الصغيرة تم اكتشافهم في القرن العشرين، لكن لماذا لا تنجذب هذه الأجسام للمشتري وتسقط به؟ لنفهم السبب لنتعرف أولاً على مصطلح نقاط لاگرنچ.

لنتخيل أن لدينا جرمين وليكن الأرض والشمس، يمكننا تحديد مدار كلا الجرمين بسهولة بمعادلات نمتلكها، ولكن ماذا إذا أضفنا جرماً ثالثاً مع الجرمين الأخرين بحيث يتأثروا بجاذبية بعضهم البعض؟ سيصبح الأمر فوضوياً وصعب توقع مدار الثلاث أجرام لفترات طويلة بمعادلة عامة، هذه المعضلة مشهورة في الوسط العلمي باسم معضلة الأجسام الثلاث، لكن في عام 1772 أتى العالم جوزيف لاگرنچ بفرضية بحيث يمكن حل هذه المعضلة في حالات معينة.

نشر لاگرنچ ورقة علمية تتضمن أنه إذا كان لدينا الجسم الأول أضخم 25 مرة على الأقل من الجسم الثاني، وكلا الجسمين أكبر بكثير من الجسم الثالث، إذا يمكننا في هذه الحالة أن نخرج بنتائج رائعة تتنبأ بمسار الجسم الثالث، والمثير أكثر أننا تمكنا من خلال نظرية لاگرنچ أن نحدد أماكن معينة إذا تواجد بها الجسم الثالث الصغير، سيكون ثابتاً بالنسبة للجسمين الأخرين للأبد ويبقى على نفس المسافة بينهم بفضل تأثير جاذبية الجرمين الأخرين حيث يكونوا بنفس قوة التأثير على الجسم الثالث.

وبتطبيق هذا المفهوم على مدارات الكواكب في المجموعة الشمسية، يمكننا أن نحدد النقاط التي شرحها لاگرنچ التي يكون فيها الجسم الصغير غير معرض لجاذبية قوية تجاه جسم واحد تدفعه نحوه، بالنسبة للأرض لدينا 5 نقاط تُدعى نقاط لاگرنچ، تبدأ من L-1 إلى L-5، في هذه النقاط إذا أرسلنا إليها جسم صغير مثل قمر صناعي سيبقى في مكانه إلى الأبد كفخ يقع به. وبالفعل لدينا سواتل ولعل أشهرهم مرصد مناخ الفضاء العميق (DSCOVR) الذي يقع في نقطة L-5 بين الأرض والشمس على مسافة مليون ونصف كيلومتر من الأرض لتصوير الأرض حيث سيكون القمر الصناعي موجهاً طوال الوقت ناحية النهار الأرضي بفضل موقعه بين الأرض والشمس الثابت.

حسناً، لنعد الآن إلى الكويكبات الضخمة التي في مدار المشتري، هذه الكويكبات تٌدعى كويكبات طروادة لأنها تكون في النقاط التي حددها لاگرنچ سابقاً، وبالتالي تبقى في هذه المنطقة للأبد ولا تنجذب في اتجاه الكوكب،

وتم اكتشاف هذه الأجسام بعد رصد متعمد من قبل العلماء في القرن الثامن عشر في نقاط لاگرنچ تحديداً لنرى هل هناك أجرام وقعت في هذا الفخ أم لا. وبالفعل هنا كانت بداية اكتشاف كويكبات طروادة الخاصة بالمشتري كما توقعوا، هذه الأجرام الصغيرة تكونت مع تكون المجموعة الشمسية وبقيت في مكانها هذا منذ ذاك الوقت.

حتى الآن نعلم أن هناك قرابة 6 آلاف كويكب طروادة حول المشتري، أجسام غامضة لم يكتشفها الإنسان بعد، لكن قريباً سنتمكن من زيارتها بفضل مركبة ناسا الجديدة لوسي (LUCY) التي من المقرر لها الإنطلاق أكتوبر 2021 لتزور 5 أجرام من كويكبات طروادة حول المشتري، وستصل لأول جرم في 2025.

بالطبع هناك كويكبات طروادة حول الكواكب الأخرى ولكن لا نعلم عنها شئ وذلك لأنها صغيرة الحجم جداً وخافتة صعبة الرصد، ربما هناك أجرام مماثلة في نقاط لاگرنچ التي حول الأرض ولكن لا نعرف عنها شئ، لكن مركبة OSIRIS-REx التي من المقرر لها الهبوط على كويكب بينو (Bennu) الذي يقع خلف مدار الأرض لتجميع عينات، عبرت بجانب نقطة لاگرنچ-4 لتصور لنا هذه المنطقة عند عبورها لعلنا نكتشف جيران للأرض منذ بدء تكون المجموعة الشمسية محاصرين في هذا المدار لكنها لم تجد شئ.

 في الثقافة العامة

• استخدمت المشكلة كحبة في ثلاثية الخيال العلمي للروائي الصيني سيكسن ليو، وتم استخدام اسم المعضلة ل الجزء الأول ولل ثلاثية ككل.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انظر أيضاً

• ميخائيل مينوڤيتش
• Gravity assist
• Low-energy transfer
• Few-body systems
• n-body simulation
• تشكل وتطور المجرات
• Triple star system
• مشكلة سيتنيكوڤ

 قراءات إضافية

• Poincaré, H. (1967). New Methods of Celestial Mechanics, 3 vols. (English trans.). American Institute of Physics. ISBN 978-1-56396-117-5.
• Aarseth, S. J. (2003). Gravitational n-Body Simulations. New York: Cambridge University Press. ISBN 978-0-521-43272-6.
• Bagla, J. S. (2005). "Cosmological N-body simulation: Techniques, scope and status". Current Science. 88: 1088–1100. arXiv:astro-ph/0411043. Bibcode:2005CSci...88.1088B.
• Chambers, J. E.; Wetherill, G. W. (1998). "Making the Terrestrial Planets: N-Body Integrations of Planetary Embryos in Three Dimensions". Icarus. 136 (2): 304–327. Bibcode:1998Icar..136..304C. CiteSeerX 10.1.1.64.7797. doi:10.1006/icar.1998.6007.
• Efstathiou, G.; Davis, M.; White, S. D. M.; Frenk, C. S. (1985). "Numerical techniques for large cosmological N-body simulations". Astrophysical Journal. 57: 241–260. Bibcode:1985ApJS...57..241E. doi:10.1086/191003.
• Hulkower, Neal D. (1978). "The Zero Energy Three Body Problem". Indiana University Mathematics Journal. 27 (3): 409–447. Bibcode:1978IUMJ...27..409H. doi:10.1512/iumj.1978.27.27030.
• Hulkower, Neal D. (1980). "Central Configurations and Hyperbolic-Elliptic Motion in the Three-Body Problem". Celestial Mechanics. 21 (1): 37–41. Bibcode:1980CeMec..21...37H. doi:10.1007/BF01230244.
• Moore, Cristopher (1993), "Braids in classical dynamics", Physical Review Letters 70 (24): 3675–3679, doi:10.1103/PhysRevLett.70.3675, PMID 10053934, Bibcode: 1993PhRvL..70.3675M, http://tuvalu.santafe.edu/~moore/braids-prl.pdf .
• Šuvakov, Milovan; Dmitrašinović, V. (2013). "Three Classes of Newtonian Three-Body Planar Periodic Orbits". Physical Review Letters. 110 (10): 114301. arXiv:1303.0181. Bibcode:2013PhRvL.110k4301S. doi:10.1103/PhysRevLett.110.114301. PMID 25166541.
• Li, Xiaoming; Liao, Shijun (2014). "On the stability of the three classes of Newtonian three-body planar periodic orbits". Science China Physics, Mechanics & Astronomy. 57 (11): 2121–2126. arXiv:1312.6796. Bibcode:2014SCPMA..57.2121L. doi:10.1007/s11433-014-5563-5.

 وصلات خارجية

• Chenciner, Alain (2007). "Three body problem". Scholarpedia. 2 (10): 2111. Bibcode:2007SchpJ...2.2111C. doi:10.4249/scholarpedia.2111.

• Physicists Discover a Whopping 13 New Solutions to Three-Body Problem (Science)
• Solar Eclipse: A Multimillenium Tale of Computation