مستخدم:Hasanisawi/اساليب الاظهار-نظرية الظلال

نظرية الظل في الاكسنومتري الكافاليرا الافقية

نظرية الظلال هي فرع من فروع الهندسة الوصفية، تستخدم في تمثيل ظلال الأجسام بالنسبة لمصدر ضوء. الظل هو منطقة محددة بمحيط مغلق ناتج عن وجود مصدر ضوء.

يمكن تعريف نظرية الظلال بالدراسة التي تسمح , عندما يثبت مصدر ضوء, بانشاء ، من خلال سلسلة من العمليات الرسومية الهندسية، الظل الذاتي والساقط لشكل ما

تم التأكيد ان الهندسة الوصفية يجب ان تؤخذ في الاعتبار من وجهتين نظر. الأولى باعتبارها وسيلة للوصول الى تحديد بدقة النتائج المرجوة، وهذه هي الطريقة التي كانت تستخدم في قطع الحجارة والنجارة. من جهة ثانية ، فهي وسيلة إظهار للكيانات الهندسية. في هذه الحالة تحديد الظلال هي ميزة مساعدة..

 تاريخ

الدراسات الأولى عن الإنشاءات الهندسية للظلال في الاظهار المنظوري تعود إلى 1600 وبالخصوص الى كتب گويدوبالدو دل مونته عن الاظهار المنظوري (Perspectivae Libri VI)ء, 1600 بيزا.

على وجه الخصوص ، بالنسبة الى الإنشاءات الهندسية للظلال في الاسقاطات المتعامدة ، من المناسب الإشارة إلى دروس all'Ecoles Normales ل غاسبر مونج (القرنين الثامن عشر والتاسع عشر). تحديد الاشكال في الفراغ وطرق اظهارها هي مهمة الهندسة الوصفية التي هدفها حدد من قبل غاسبر مونج منذ البداية. من ضمن الرسومات التي نفذها مونج كان هناك أيضا جزء يتعلق بنظرية الظلال. على بينة ان الرسوم ليس لها معنى عندما تفتقر إلى تأثيرات الظلال. . ومن الواضح ان الرسم مهما كان دقيق ولكنة يفتقر للظلال, يبدو غامض وغير محدد.

الاطروحات في مجال الهندسة الوصفية بعد مونج, تضمنت العديد من الدراسات التي كرست حيزا واسعا لموضوع الظلال، مثل، دراسات فاليه (1821- Vallee) ، هاشيت (1828Hachette) ، بيليت (1885 Pillet) .

تم الانتهاء من عملية الترميز في اطروحة المنظور الخطي (Traite’ de la Perspective Lineaire) من عمل لا گورنير (La Gourneire -1862)

وقد نشرت في نظرية الظلال والكياروسكورو دراسات مثيرة للاهتمام في ايطاليا من قبل تساري (Tessari 1880) , و بونتشي (Bonci 1937) .

دراسات الظلال والكياروسكورو

استخدام الظلال في الفن ، سمح, منذ نشأتة, بزيادة الشعور بالواقعية من خلال محاكاة العمق في الرسومات. ويمكن أن يُعزى اول استخدام للظلال في تاريخ الرسم إلى مازاتشو (Masaccio)، حيث الاشكال تبدو أحجام حقيقية.

القديس-بطرس-يشفي-المرضى-بظله, وهي عنوان لوحة للفنان مازاتشو -1426-1427

 الظل في الاظهار الهندسي

الظلال في التمثيل الهندسي يطبق لإعطاء ادراك بعمق الفراغ، اي لخلق وهمية البعد الثالث على سطح الرسم، وأيضاً لإعطاء صورة صحيحة عن موضع الجسم في الفراغ. ولهذا فعملية التظليل تتطلب معرفة دقيقة بقواعد الهندسة الوصفية, لتكوين الفراغ المعماري.

نظرية الظل ، هي احدى المواضيع الأكثر شمولية للمفاهيم الأساسية للهندسة الوصفية والتي يمكن ملاحظتها دائما كظاهرة طبيعة ، وبالتالي تسمح للطالب-المعماري فهم معظم المفاهيم التي عادة ما تناقش خلال الدروس. في الواقع ، نظرية الظل تضم معظم مفاهيم الهندسة الوصفية كأساليب الإسقاط ، مسائل التقاطع, ، والتألف التواحدي (Bijection) ، الخ.

ظل كيان ناتج من مصدر طبيعي ، يمكن اعتبارة اسقاط متوازي من مركز لانهائي , ويمكن ايضاً اعتبارة اسقاط مركزي إذا كان مصدر الضوء اصطناعي , أي اسقاط من مركز نهائي. وبالإضافة إلى ذلك ، ظل كيان ما ، يمكن ان يفسر ويحدد كتقاطع بين كيانات هندسية مختلفة (بين خط وسطح, او بين اسطح). بكلمات اخرى, يمكن تفسير الظل كتقاطع كيان ضوء (خط مستقيم ، سطح مستوي، أو سطح منحني) مار بالكيان المعتبر (نقطة ، خط ، شكل) مع كيان متلقي للظل (سطح مستوي او منحني)

 أنواع الظلال

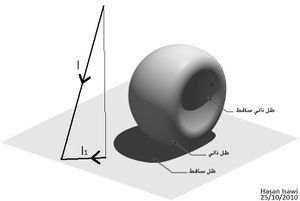
وفقاً للسطح (أو السطوح) الذي يستقبل الظل بالنسبة للجسم الماخوذ في الاعتبار, هناك ثلاثة تسميات للظلال، وهي:

• ظل ذاتي (shade): هذا هو الجزء من K الغير معرض للضوء.
• ظل ساقط (shadow): هو اسقاط لحدود الظل الذاتي على الأسطح المجاورة.
• ظل ساقط ذاتي (بالإيطالية:ombra autoportata): هو إسقاط لحدود الظل الذاتي على سطح نفس الجسم K.

 خلفية علمية

في الفقرات التالية، هناك خلفية علمية (اسقاطية) أتاحت للهندسة الوصفية رسم الظلال في طرق الاظهار المختلفة (منظور, اكسنومتري, مونج). أي الانشاءات الهندسية التي تأخذ في الاعتبار الاحتياجات الحقيقية عند ممارسة الرسم.

بالإضافة إلى المواضيع المتعلقة بإجراءات الرسم التقليدي، يتناول هذا النص التطورات الراهنة لنفس الموضوع. الذي مع ظهور أدوات الرسم الرقمي, لا يستخدم تلك الاجراءات في عدة إسقاطات فردية، ولكن من خلال عمليات اسقاط تلقائية لاي أي شكل من الأشكال على أي سطح. هذة العمليات تنفذ على نموذج افتراضي من واحد أو أكثر من مصادر الضوء, التي من الممكن انشائها في العديد من برامج الكمبيوتر المختصة. وبالإضافة إلى ذلك، في الحاسوب، أثر التصيير (Rendering) يسمح بدراسة مفصلة للمواد وكيف تتصرف عند التعرض للضوء وتشكيل الظل. وبالتالي على ما يبدو مواجهة هذة الإجراءات الرسومية غير ضرورية، ولكنها تسمح للمصمم إدارة واعية للظلال المتولدة تلقائياً, والتحكم بمنطق البرنامج المستخدم، وإلا فهو غير قادر على التدخل لاجتياز العقبات التي, كما هو معروف ، تظهرها كل الادوات. هذه العقبات تؤدي الى اعتماد الخيارات والحلول الوسط للوصول, في الحالات المختلفة, الى تحقيق نتائج مفروضة: لهذا يجب معرفة المفهوم وتطبيقاته من أجل اتخاذ قرار الحل المناسب لكل حالة.

وعلاوة على ذلك ، الظلال تثري رسم السكتشات السريعة لإعطاء الفكرة الاولية لمشروع ما. والتي بعد ذلك ستحدد بدقة من خلال النمذجة الرقمية. كما في هذه الحالة, للحصول على رسومات واقعية، هناك الحاجة إلى معرفة كيفية تحديد ظل الأشكال والتكوينات المكانية الأكثر شيوعا.

غالبا الظلال تسمح باستكمال المعلومات ثلاثية الأبعاد لشكل ما، لأنها تعتبر رؤيا من مركز إسقاط أخر، أي أن هناك اسقاطين لنفس الشكل: مركز الاسقاط الاول يتطابق مع مركز النظر والاخر مع مصدر الضوء. في كلتا الحالتين ، من الضروري معرفة مفاهيم "عمليات الاسقاط والتقاطع" (operazioni di proiezioni e sezioni) لضمان تحقيق النتائج المرجوة. أو السماح لأفضل قراءة لنتائج الرسم واستبعاد غير مفهومة ومتناقضة أحيانا وغير ملائمة في كثير من الأحيان من من وجهة نظر جمالية.

تطبيقات الظلال في الاظهار تسمح بانشاء الرسم التقني مثل الخطة الحجمية (Volumetric plan) حيث تراكب الظل والخطة يعطي المعلومات المفقودة, ألا وهي ارتفاعات الاشكال الممثلة. ويمكن استخدام الظلال لزيادة تاثير وهمية البعد الثالث في الخطة والعلو ، والاكسنومتري والمنظور. والتي يمكن الحصول عليها بواسطة الرسم التقليدي او الرقمي.

 الأسس الاسقاطية

نظرية الظل وتطبيقاتها في أساليب الاظهار: اسقاطات مونج والاكسنومتري الكافاليرا الافقية

العناصر المرجعية هي مصدر الضوء الذي تتفرع منة أشعة الضوء ( والتي للتبسيط تعتبر خطوط مستقيمة)، الشكل الذي يستقبل الضوء والمستوى حيث يقع الظل. كفاف الظل لشكل ما , يعرف كمحموعة من نقط تقاطع أشعة الضوء الماسة ذلك الشكل مع المستوى المتلقي للظل. لرسم الظلال ضروري تحديد "الخط فاصل الظل" الذي يشير إلى الخط الذي يفصل بين منطقة الظل ومنطقة الضوء لمجسم ما. إسقاط الخط فاصل الظل على سطح، يحدد كفاف "الظل الساقط" على نفس السطح. يمكن اعتبار الخط فاصل الظل كالكفاف الظاهر بالنسبة لمركز نظر متطابق مع مصدر الضوء. الذي يمكن ان يكون نقطة لانهائية مثل الشمس ، وفي هذه الحالة أشعة الضوء تكون موازية لبعضها البعض, أو انها تتقارب، عندما يكون مصدر الضوء نقطة نهائية مثل المصباح. ومن الممكن تمييز "الظل الذاتي الساقط" بظل الكيان الذي يقع على سطح نفس الكيان.

ظل ذاتي, ظل ساقط, خط فاصل الظل, كفاف الظل الساقط

يمكن ملاحظة أنه لا توجد مناطق في الظل تماما أو في الضوء تماما ، ولكن هناك تدرجات من الضوء الى الظل. قانون جيب التمام او قانون لامبرت يحدد العلاقة بين كثافة الضوء لسطح ما والزاوية بين الأشعة الضوئية مع الخطوط العمودية على نفس السطح. يمكن ايجاد تطبيقات لهذا القانون في اظهار مستويات مختلفة الميلان بالنسبة لمصدر ضوء, او في تدريج كثافة الضوء على سطح منحني.

في الواقع ، كثيرا ما يحدث أن كيان يتلقى الضوء من مصادر مختلفة. وهذا يعني أن هناك مناطق من الكيان تتلقى ضوء من كل المصادر، والبعض من مصدر واحد والبعض الآخر لا يتلقى أي ضوء. في هذه الحالة يمكن ملاحظة الكرة مضائة من مصدر واحد (شكل) ، ثم الكرة نفسها تظهر آثار الإضاءة المجموعة (الشكل) من مصدرين ضوء مختلفين S1 و

Di seguito si vuole esplorare I vari concetti della geometria descrittiva applicati sopratutto con la modellazione 3d, In particolare i concetti che ci permettono di determinare l’ombra propria e portata di una entità geometrica. Durante il percorso si faranno spiegazioni ed analisi dei vari casi di ombre, con il fine di evidenziare i vari concetti utilizzati e la loro utilità in funzione dell’obiettivo generale del rinnovamento dell’insegnamento della geometria descrittiva . Questo problema sarà affrontato cercando di integrare i concetti della geometria descrittiva con la modellazione solida

 الظل والهندسة الاسقاطية

قبل مواجهة بعض الإجراءات لتحديد الظل في الطريقة التقليدية (أو من خلال الرسم ثنائي الأبعاد *) , فانة مثير للاهتمام ، دون اعتبار اداة الرسم المستخدمة ، معرفة ان تكوين الظل يكمن في العلاقة التي تنشأ بين الشكل في الفراغ ومسقطة على مستوى ما. حيث مصدر الضوء في هذه الحالة يتطابق مع مركز الإسقاط.

كيان يتلقى ضوء من من مصدر ضوء واحد أو من مصدرين مختلفين

ظل ذاتي, ظل ساقط ذاتي, ظل ساقط

لذلك في الفقرات التالية سوف نتعامل مع تشكيل الظل دون الاخذ في الاعتبار طريقة تمثيلها في أساليب الاظهار المختلفة (مونج, اكسنومتري,منظور) والتي ستناقش بشكل منفصل.

تحديد كفاف ظل لشكل ما يعتمد على نفس المبدأ الاسقاطي الذي هو أساس أساليب الاظهار المختلفة. مثلاً الإسقاط P' لنقطة P , على مستوى π , من مركز S , يُحدد بواسطة عمليات الاسقاط والتقاطع. أي, الإسقاط في عملية إيصال النقطتين P و S ؛ والتقاطع في ايجاد نقطة التقاطع P' بين الخط P - S والمستوى π. اذا استبدلنا مركز الإسقاط C بمصدر الضوء S, والظل P* بالاسقاط P' يمكننا ملاحظة أن عملية تحديد الظل مطابقة لعملية الإسقاط.

والإشارة إلى التشابه بين الظل والإسقاط ، فيمكن اعتبار الظل الناتج عن مصدر طبيعي (والذي يفترض أنة يقع في اللانهاية) إسقاط متوازي ( او اسطواني), مثل طريقة مونج, الاكسنومتري والمنظور، في حين ان الظل الناتج عن مصدر ضوء اصطناعي يمكن اعتباره إسقاط مركزي (او مخروطي), مثل الاسقاط ألمنظوري.

هذا التمييز مفيد لاعتماد نظام الإسقاط المناسب في تتبع كفاف الظل الساقط. والتي يمكن اعتبارها في أساليب الإظهار المختلفة كعملية إسقاط في الإسقاط.

عند التحقق من وجود علاقة اسقاطية بين العناصر المتورطة في إيجاد الظل ، يمكن تحديد العلاقة بين الكائن وظله. العلاقة بين شكل مسطح ∆ وظلة ∆* تعتبر تقابل تألفي (او افّيني) عندما يكون مصدر الضوء نقطة لانهائية ، حيث محور التقابل هو خط التقاطع بين مستوى الشكل ∆ والمستوى الذي يتلقى الظل، ومركز التقابل هو مصدر الضوء نفسه. بينما اذا كان المصدر نقط نهائية ، لا تتغير عناصر التقابل التي هي المحور u والمركز U, ولكن التناظر يسمى تقابل منظوري. بمجرد الانتهاء من تحديد متطلبات التقابل : المركز U والمحور u ونقطتين متقابلتين (أو خطين متناظرين) ، يمكن المضي قدما لتحديد نقاط ظل أخرى من خلال استغلال خاصية التقابل ، التي تكمن في اصطفاف النقاط المتناظرة مع المركز U وفي تقابل الخطوط المتقابلة على طول المحور u. على سبيل المثال ، بمجرد إيجاد نقطتين متقابلتين مثل A* و A (الشكل --)، يمكن تحديد الظل B*: (للنقطة B ) بتوصيل النقطتين A و B بواسطة الخط r , الذي يلتقي المحور u في النقطة t'α. والتي بتوصيلها A* نجد الخط r* ( ظل الخط r ) , الذي يتقاطع في النقطة B* (نقطة الظل المطلوبة) مع شعاع الضوء المار بالنقطة B .

تقابل تألفي بين شكل وظلة

 الظل كعملية تقاطع بين كيانات هندسية

يمكن تفسير الظل كعملية تقاطع بين كيان ضوئي مع كيان متلقي للظل. الكيان الضوئي يمكن أن يكون خط في الحالة التي يراد فيها إيجاد ظل نقطة , ويمكن ان يكون سطح مستوي أو منحني عندما يراد إيجاد ظل خط مستقيم أو منحني. ويمكن صياغة هذه الحالات كالنحو التالي :

• ظل نقطة P على سطح ∆ يمكن تحديده كنقطة تقاطع بين الشعاع الضوئي المار بالنقطة P مع السطح المتلقي الظل ∆
• ظل خط مستقيم r على سطح ∆ يعادل تقاطع بين مستوى ضوئي مار بالخط r والسطح ∆.

ملف:اسم الصورة

تعليق

• ظل مضلع θ على سطح ∆, يعادل تقاطع بين منشور ضوئي والسطح ∆. حواف المنشور تتكون من أشعة الضوء وقاعدته تتطابق مع نفس المضلع θ.
• ظل خط منحنى κ على سطح مستو α، يتوافق مع تقاطع بين اسطوانة ضوئية والسطح α . سطح الاسطوانة تتكون من أشعة الضوء وقاعدته تتطابق مع نفس المنحنى κ.

 أمثلة

الرسومات المبينة في هذا البحث, نفذت باستخدام أوتوكاد 2006 ، والتي يُراد بها أن تكون أمتله لطريقة جديدة في تدريس مفاهيم للهندسة الوصفية المختلفة (مثل مسائل التقاطع ، والقياس ، والموضع والمستويات المساعدة). والتي حسب الموضوع المواجهة, هذه النماذج يمكن ان تحتاج الى القليل او الكثير من العمليات التحضيرية من الإنشاءات الهندسية. بعد مرحلة توليد النماذج تأتي عادة المرحلة التعليمية الرئيسية والتي تكمن في تحليل هذة النماذج, بواسطة انشاءات هندسية اضافية, بهدف تفسير المفاهيم النظرية من جهة ، وتوضيح وتبرير النتائج التلقائية التي تمثلها النماذج. مثلاً, بعد عملية تحضير العناصر الرئيسية لتوليد نموذج مخروط دائري, وتلك لتوليد ظلالة الذاتية والساقطة, تاتي العملية التحليلية, من خلال الانشاءات الهندسية الاضافية, لتفسير وتبرير كيف تمت عملية نمذجة المخروط وكيف تم ايجاد ظلالة. وفي هذا الصدد ، ينبغي الاخذ في الاعتبار أنه من اجل توليد بعض النماذج النظرية هناك الحاجة الى عمليات تحضيرية مجهدة من الانشاءات الهندسية. كما هو الحال مثلاً في العمليات التحضيرية لتوليد الاسترداد المنظوري (geometric restitution of perspective) وفي الانشاءات الهندسية لايجاد التماس بين ثلاثة مخروطيات, او في النمذجة الاسطح الكعكية براسم متغير، او الأسطح المسطرة .

الغرض من هذة الطريقة الجديدة في تعليم مفاهيم الهندسة الوصفية، هو تحفيز الطالب على التركيز في متابعة الانشاءات الهندسبة التي تمثلها تلك المفاهيم بطريقة سريعة وممتعة.

طريقة تحث الطالب على ان يكون فعال في الوصول مباشرة الى النتائج المرجوة وليس بواسطة العديد من المحاولات كما يفعل الكثيرون من مستخدمين برامج الرسومات الحاسوبية, والذين عادة ما ينتجون نماذج متشابهة ،متكررة ، ودون أي أسس نظرية. أولئك الذين يدرجون باستمرار النماذج مسبقة الصنع المخزنة في هذة البرمجيات. وبالتأكيد حدث للاغلبية منا رؤية اظهارات معمارية مليئة بألالوان والعناصر البيئية (السماء والأشجار والناس والسيارات), التي تخفي تقريباً كلياً النماذج التي تمثلها تلك العمارة

الطريقة الجديدة في تدريس الهندسة الوصفية ستساعد الطالب على التفكير النقدي لاكتشاف طرق جديدة في التحكم بادوات الرسم الرقمية واستخدامها للوصول الى تحقيق النتائج المرجوة.

وبالإضافة إلى ذلك ، هذه الطريقة الجديدة في تدريس الهندسة الوصفية ، مع الاستخدام الحكيم للأدوات الرقمية ، يمكن أن تعطي فرص جديدة وخاصة في مجال البحث العلمي في إعادة تقييم النظريات القديمة واكتشاف نظريات جديدة عن طريق استغلال لدقة الادوات الرقمية. ولإعطاء الهندسة الوصفية إمكانية ابتكار أشكال هندسية جديدة والتحقق من خصائصها الهندسية لاستخدامها المحتمل في معرض العمارة الحديث. وكما قال مونج ، الهندسة الوصفية تعلم كيفية اكتشاف المجهول بدءا من المعلوم

في الفقرات التالية هناك أمتله لبعض حالات التقاطع بين كيان ضوئي وكيان متلقي للظل.

 ظل نقطة P على سطح مستوي ( أو منحني) كتقاطع بين شعاع الضوء والمستوي

مثال 1: ظل نقطة على مستوى عام

ظل نقطة على سطح مستوي مائل

يتم تحديد ظل نقطة P على مستوى عام α (ألفا) كنقطة تقاطع بين شعاع الضوء المار بالنقطة P والمستوى المتلقى الظل α.

لتحديد *P كظل للنقطة P يجب فهم واتباع الإجراءات التالية:

• 1- نمرر بالنقطة P شعاع ضوئي l
• 2- نمرر بشعاع الضوء l مستوى مساعد رأسي λ
• 3- نحدد خط التقاطع بين المستويات ألفا وبيتا
• 4- في النهاية نجد نقطة التقاطع P* (وهو المطلوب) بين الخطوط r و s.

Commenti con riferimento alla modellazione 3d Per quanto riguarda la scelta di utilizzare, tra gli infiniti piani passanti per il raggio luminoso e secante la superficie ricevente l'ombra, un piano verticale, può essere meglio giustificata nel disegno bidimensionale e nella modellazione Wireframe e anche nella modellazione superfici, dove occorrono delle costruzione geometriche per determinare il risultato della sezione tra il piano di luce e la superficie, che saranno molto più semplificata col scegliere un piano verticale. Invece nella modellazione solida, una volta finito di generare il modello, la determinazione della sezione avviene in modo automatico, e che puo essere ottenuta specificando qualsiasi piano secante la sfera e passante per il raggio. In questo caso l’individuazione del piano e’ semplice, dato che un piano e' individuato da tre punti non allineato, e’ sufficienti specificare due punti del raggio luminoso passante per P, ed il terzo punto può essere specificato a piacere nello spazio. La scelta di utilizzare un piano di luce verticale può essere giustificata dal solo fatto di visualizzare un piano famigliare e facilmente riconoscibile.

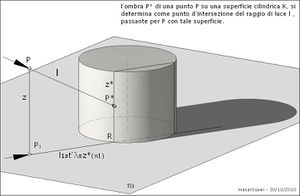
مثال1(1): ظل نقطة على سطح اسطواني بمحور رأسي

ظل نقطة على سطح اسطواني

يتم تحديد ظل نقطة P على مستوى اسطواني K كنقطة تقاطع بين شعاع الضوء المار بالنقطة P وذلك السطح المتلقى الظل. لتحديد ظل النقطة P ينبغي اتباع الاجراءات التالية:

• – نمرر بالنقطة P شعاع ضوئي l
• -- نمرر بشعاع الضوء l مستوى مساعد رأسي λ
• – نحدد خط التقاطع z* بين المستوى المساعد لامدا والسطح K
• -- في النهاية نجد نقطة التقاطع P* (وهو المطلوب) بين الخطوط z* و s.

ملاحظة : لتسهيل بشكل عام ، تحديد ظل نقطة P على سطح أسطواني K، خصوصاً في الرسم التقليدي (اي ثنائية الأبعاد), من الأفضل اختيار خط g موازي لمحور الاسطوانة, لأن ظل g سيكون موازي لمحور الأسطوانة. للحصول على ظل g في هذه الطريقة, ينبغي تحديد نقطة التقاطع Q للخط g مع مستوى قاعدة الاسطوانة. ثم تحديد ظل نقطة ثانية ( مثل P) لايجاد ظل الخط m على نفس مستوى القاعدة. بتوصيل النقاط R و P*(δ) نجد m*(δ (ظل m على مستوى القاعدة). نتابع بإيجاد نقطة التقاطع R بين الخط m*(δ وقاعدة الاسطوانة. ومن هذة النقطة R نرسم g* ظل الخط g على السطح الاسطواني بحيث يكون, كما قلنا سابقاً, موازي لمحور الاسطوانة. وأخيراً نجد النقطة P* كما هو مطلوب , كتقاطع بين الشعاع الضوئي المار بالنقطة P والخط m*.

ظل نقطة على سطح اسطواني بمحور افقي

ظل دائرة ∆ على سطح مستوي 1π يمكن أن يُحدد كتقاطع بين اسطوانة ضوء (بقاعدة ∆) مع المستوى 1π لذي يتلقى الظل.

مثال 3: ظل نقطة على سطح مخروطي

ظل نقطة على سطح مخروطي

ظل نقطة P على سطح، سواء مستوي أو منحني ، يتم بتحديد نقطة التقاطع بين شعاع الضوء المار بالنقطة P وذلك السطح المتلقى الظل.

• منذ ان نقطة التقاطع P (ظل النقطة P) تحدد باستخدام مستوى ضوء λ يمر بالنقطة P ويتقاطع مع السطح المتلقى الظل وفقاً لخط , الذي يمكن ان يكون مستقيم أو منحني. في الحالة التي يكون فيها السطح مستوي ، يسهل تحديد خط التقاطع, ويصعب تحديدة في حالة السطح المنحنى ، على الأقل في الرسم التقليدي (أو بالأحرى في الرسم ثنائي الأبعاد).

في هذه الحالات ، ولتسهيل عمليات الانشاءات الهندسية, هناك الحاجة إلى معرفة الخصائص الهندسية للسطح المعني، أو بالاحرى معرفة ماهية التكوين الهندسي لذلك النوع من الاسطح ، من أجل الحصول، إذا ممكن ، على مقاطع سهلة التحديد. على سبيل المثال ، في حالة السطح المخروطي، المقاطع الأكثر بساطة تتكون من خطوط مستقيمة, يحصل عليها باستخدام مستويات مارة بقمة ذلك السطح. الأسطح المخروطية تشمل جميع أنواع المخاريط (بما في ذلك الاسطوانة كحالة خاصة للمخروط) التي تسمح بايجاد في كل نقطة منها مقطع مخروطي (بما في ذلك النقطة ، والخط كحالات اسثنائية للمخروطيات). بالاشارة الى المسألة في الشكل ، ظل نقطة P ، او بالاحرى نقطة تقاطع بين شعاع الضوء المار بالنقطة P والمخروط K , يحدد باستخدام مستوى ضوء λ بحيث يمر بالنقطة P وبقمة المخروط. بهذة الطريقة, المستوى λ يقطع المخروط وفقاً لخطيين. التي يمران بقمة K وبالتوالي بنقطتين من قاعدة K. للعثور على هذه النقاط يجب علينا تحديد خط التقاطع P*-V* , (والذي في هذه الحالة يتطابق مع الاثر الاول للمستوى λ) بين مستوى الضوء λ ومستوى القاعدة π1 , الخط P*-V*. يحدد من النقطتان P* و V*, والتي تمثل بالتوالي، P* ظل النقطة المعينة على مستوى القاعدة و V* ظل القمة نفس المستوى. حيث الخط P*-V* يقطع القاعدة نجد النقطتان R Q , بتوصيل هاتان النقطتان بالقمة نجد خطان التقاطع بين المخروط ومستوى الضوء λ . وأخيرا نجد النقطة المطلوبة P* ( ظل النقطة P) كتقاطع بين خط الضوء l وخط التقاطع V*-R (راسم سطح المخروط).

مثال 3: ظل نقطة على سطح كروي

ظل نقطة على سطح كروي

ظل نقطة P على سطح كروي الشكل ، يُحدد كتقاطع بين شعاع الضوء l المار بالنقطة P وذلك السطح.

الإجراء هو الأتي:

• نمرر بالنقطة P شعاع ضوء l ؛
• نمرر بالشعاع l مستوى رأسي λ؛
• نحدد دائرة التقاطع بين المستوى λ والكرة ؛
• نحدد نقطة التقاطع P* بين الدائرة والشعاع l.

رسم ظل نقطة على سطح كروي بالطريقة التقليدية

من بين أنواع الاكوسنمتري المختلقة ، تم اختيار استخدام الأكسونمتري الكافاليرا الافقية ، لسهولة تنفيذها ، والتي تعود الى تطابق بين مستوى الاسقاط الاكسونمتري والمستوى الاول للاسقاط المونجي. وبهذا, الاشكال التي تنتمي الى مستويات أفقية تبقى, بعد الاسقاط بمقاسها وشكلها الحقيقي، وتعود أيضاً الى أنه يمكن تقليص القياسيات الرأسية على النحو المرغوب فيه أو تركها بمقاسها الحقيقي (بالنسبة لمقياس الرسم) . لهذه الأسباب، ولحقيقة أنه يجب تعليم الطالب-المعماري، نوع من التمثيل ثلاثي الأبعاد، سهل وسريع الأداء, حتى في الرسم الحر، تم تفضيل استخدام هذا النوع من الأكسونمتري في التطبيقات النظرية للرسم في الأسلوب التقليدي.

لتمثيل ظل كرة ,وظل نقطة عليها في الاكسنومتري الكافاليرا, يمكن تقسيم مراحل هذة المسألة كما يلي :

• المرحلة الأولى : التمثيل الاكسنومتري للكرة
• المرحلة الثانية : تمثيل الظلال، بما في ذلك ظل الذاتي والساقط للكرة وأيضاً ظل نقطة على نفس الكرة

المرحلة الأولى : التمثيل الاكسنومتري للكرة

أكسونمتري كافاليرا افقية (military axonometry) للكرة عن طريق تحديد الكفاف الظاهر ، وبعض دوائر العرض

تمثيل الكرة يتطلب تحديد بعض العناصر الهامة مثل القاعدة ، عدد من دوائر العرض لمحاكاة انحناء الكرة ، والكفاف الظاهر. وبالنظر إلى خصائص هذا النوع من الاكسنومتري ، يمكن رسم بسرعة الدائرة الاستوائية Δ بنصف قطر محدد سلفا. أما الدوائر الي تمثل دوائر العرض فينغي تحديدها كمقاطع بين الكرة ومستويات أفقية متساوية البعد عن بعضها البعض. وهذا لاعطاء مظهر منحنى منتظم للكرة. وبافتراض تقليص وحدة قياس المسافات الرأسية, اتجاه الإسقاط يكون بزاوية أكبر من 45 درجة بالنسبة لمستوى الإسقاط. عملياً، نثبت على المحور الرأسي a للكرة، النقطة N, التي تمثل أعلى نقطة للكرة, على مسافة من مركز الكرة C يساوي ، على سبيل المثال, قيمة أقل من نصف قطر الدائرة الاستوائية Δ . بما ان عرضيات الكرة, في هذا النوع من الاكسنومتري , كما قلنا سابقاً, تبقى بعد الاسقاط بقياس وشكل حقيقي، فانة كافي تحديد مواقع مراكز ومقاسات أنصاف الاقطار لرسم دوائر العرض.

علماً ان اطراف انصاف اقطار هذة الدوائر, هي نقط تقاطع خطوط أفقية، على التوالي ، مع المحور a للكرة ومع سطحها. فلنفترض ان هذه الخطوط تنتمي الى مستوى رأسي γ يمر بمركز الكرة ويوازي اتجاة مركز الاسقاط. لتعيين نقاط التقاطع ينبغي إيجاد الدائرة الطولية Ф كتقاطع بين γ والكرة. وبما ان الاسقاط الاكسنومتري للدائرة Ф يتطابق مع الاثر t'γ للمستوى γ . فينبغي قلب γ على مستوى الاسقاط, باستخدام t'γ كمحور للانقلاب, وبهدف توضيح عمليات الانشاء الهندسي الضرورية تم نقل الانقلاب، كما هو موضح في الشكل, الى الجانب الايمن من الاسقاط الاكسنومتري. ومن المهم الإشارة إلى أن نتيجة عمليات الانقلاب والنقل تعادل عملية الإسقاط الثالث المونجي (Mongian projection) . ,ونتيجة وجود تماثل للكرة بالنسبة لمستوى الاسقاط, فقد تم رسم الجزء العلوي فقط. حيث المسقط الثالث للمحور a عمودي على t'γ ويمر بالمركز C. المستقيم C-(N) الذي ينتمي إلى المحور a ، تم تقسيمه إلى أجزاء متساوية في النقاط (1) ، (2) ، (3) التي تمثل الإسقاط الثالث لمراكز دوائر العرض. من هذه المراكز تمر الخطوط الأفقية التي تتقاطع مع الدائرة (Ф) في النقاط 4،5،6 . وبهذه الطريقة تم الحصول على مقاسات أنصاف أقطار دوائر العرض. على سبيل المثال ، الدائرة التي مركزها النقطة 1 ، نصف قطرها يساوي المستقيم 1-4. وبالمثل ، تم رسم دوائر العرض الأخرى. والجدير بالذكر أنة كلما كان اكثر عدد دوائر العرض كلما كان أفضل محاكاة انحناء الكرة.

الكفاف الظاهر للكرة يمكن أعتباره تقاطع بين مستوى الاسقاط واسطوانة محاطة لنفس الكرة. حيث محور الاسطوانة, في الإسقاط الثالث, مواز لاتجاه الخط (N)-(N)’ , , والخط الماس الدائرة (Ф)، في النقطة (T) ، يمثل واحد من راسمين الكفاف الظاهر للأسطوانة. هذا الراسم يتقاطع مع خط الارض في النقطة (T') ، والتي إسقاطها الاكسنومتري يمثل واحد من طرفين المحور الأكبر لاهليج الكفاف الظاهر. المحور الأصغر معلوم سابقاً لأنة متطابق مع قطر الدائرة Δ المتعامد على المحور الاكبر. بهذه الطريقة وبمجرد تحديد هذه المحاور يمكن رسم الاهليج الذي يمثل الكفاف الظاهر للكرة.

المرحلة الثانية : تمثيل الظلال، بما في ذلك ظل الذاتي والساقط للكرة وأيضاً ظل نقطة على نفس الكرة

ظل ذاتي وساقط للكرة وظل نقطة على نفس الكرة

بمجرد الانتهاء من تمثيل الكرة في الاكسنومتري الكافاليرا الأفقية (كما ورد أعلاه) ، وكذلك النقطة P ، وتم تعيين اتجاه شعاع الضوء l واسقاطة الاول l1, يمكن متابعة العمليات بالترتيب التالي :

• ظل نقطة P على الكرة
• ظل ذاتي وساقط للكرة

• يتم تحديد ظل النقطة P على الكرة كتقاطع بين الكرة وشعاع الضوء المار بالنقطة P. ولهذه الغاية, نمرر بالنقطة P مستوى ضوء λ . الاثر الاول لهذا المستوى يتطابق مع الإسقاط الاول l1 للشعاع l . ونحدد التقاطع الدائري Θ بين λ والكرة. ولكن بما ان Θ تنتمي إلى مستوى غير موازي لمستوى الاسقاط 1π ، فصورتها الاكسنومترية تكون اهليج. وكما هو معروف رسم الاهليج يتطلب بعض الانشاءات الهندسية ، فلتفادي هذه الإنشاءات يمكن الاستفادة من خاصية هذا النوع من الاكسنومتري، من خلال إجراء إسقاط مونجي على مستوى رأسي موازي للمستوى λ , ومن ثم نقوم بعملية قلب مستوى الاسقاط المونجي لرسم الدائرة Θ بشكلها ومقاسها الحقيقي. عمليا، نرسم خط الأرض L.T بحيث يكون موازي للاثر الاول t'λ للمستوى λ ، ومن ثم نسقط على L.T نقاط تقاطع ∆ مع t'λ . هذة النقط تمثل قطردائرة التقاطع Θ . نسقط أيضا شعاع ضوء لتحديد نقطة التقاطع P*2 بين Θ2 و L2 . ومن ثم نقوم هذه النقة P*2 لايجاد موضعها الاكسنومتري P* , والتي تمثل ظل النقطة P على الكرة.

• لتحديد الظل الذاتي للكرة ، نأخذ في الاعتبار أن فاصل الظل للكرة، ينتمي إلى مستوى α عمودي على شعاع الضوء ومار بمركز الكرة. في هذة الحالة, فاصل الظل هي الدائرة Σ والتي تتحول الى اهليج في هذا النوع من الاسقاط الاكسنوكتري. لإيجاد هذا الاهليج Σ, نعمل في الإسقاط المونجي ، بتمرير الخط m2 بشكل عمودي على الاسقاط l2 لشعاع الضوء l. الخط m يمثل خط أقصى ميلان للمستوى α ويمثل ايضاً واحد من الاقطار المتزاوجة للاهليج Σ . نقطة التقاطع M2 بين الخط m2 وكفاف الكرة في الاسقاط المونجي , يمثل نقطة أقصى ارتفاع لفاصل الظل Σ. حيث يمكن تقويم ارتفاع هذه النقطة M2 ومن ثم نقلها الى موضعها الاكسنومتري لايجاد النقطة M التي تمثل طرف القطر m, القطر الأخر g للاهليج فاصل الظل Σ يتطابق مع قطر الدائرة الاستوائية ∆ ويكون عمودي على الاسقاط الاول m1 للخط m.

وبمجرد الانتهاء من ايجاد اثنين m و g من الأقطار المتزاوجة, يمكن القيام بالاجراء المفصل في الشكل -- لانشاء الاهليج Σ.

• لتحديد الظل الساقط للكرة، نفترض وجود مستوى افقي δ حيث ترتكز الكرة في الطرف السفلي لمحورها. نتابع الإجراء بإيجاد الظلال m* g* للأقطار m g . والتي في هذه الحالة تمثل أيضا محاور الظل الساقط Σ* للاهليج Σ.

ومن الجدير بالذكر أن الظل الساقط Σ* لكرة على مستوى δ هو تقاطع بين المستوى δ واسطوانة دورانية مقطعها القائم فاصل الظل Σ ومحورها شعاع الضوء المار بمركز الكرة.

 ظل خط مستقيم r على سطح مستوي ( أو منحني)

مثال 1: ظل خط عام r على مستوى عام α

ظل خط عام r على مستوى عام α

لتحديد ظل الخط r على المستوى α ، ينبغي تحديد ظل نقطتين من r على α

• 1- لتحديد ظل النقطة الأولى P ، نبدأ على النحو التالي :
• - ظل النقطة P يُحدد كنقطة تقاطع بين شعاع الضوء l المار بالنقطة P والمستوى α . للقيام بذلك - نمرر بالشعاع l مستوى رأسي β , - نحدد خط التقاطع s بين المستويين β و α . وهكذا نجد P* ( ظل P) كنقطة تقاطع بين الخط s والشعاع l.
• 2- لتحديد ظل نقطة ثانية للخط r على α ، يمكننا ان نتابع كما يلي :
• - نجد ظل الخط r على π1 (مستوى الإسقاط الأول) بتحديد وتوصيل النقطتين T’r ( الأثر الأول للخط r) و P*(p1) (ظل النقطة P على π1) . من المهم ملاحظة ان ظل الخط r على π1 يمثل خط تقاطع مستوى الضوء λ المار بالخط r مع π1, والذي يسمى الأثر الأول للمستوى λ ويرمز له t'λ.
• - نجد نقطة التقاطع R بين الآثار الأولى (t'α و t'λ ) للمستويات α و λ . النقطة R تمثل ظل نقط ثانية للخط r على المستوى α. لذلك نجد r* (ظل الخط r على α), بتوصيل النقطتين P* و R . وأخيراً, نجد Q* (ظل الطرف الأخر للخط r) كنقطة تقاطع بين r* وشعاع الضوء المار بالنقطة Q

 الظلال كمقاطع مخروطية

ظل خط مستقيم على سطح مخروطي يمكن أن يكون قطع مخروطي (ربما متدهور). ووفقا لميلان مستوى الضوء λ (المار بالخط) بالنسبة لرواسم المخروط ، القطع المخروطي يمكن أن يكون على التوالي :

• قوس قطع ناقص ، عندما مستوى الضوء λ يقطع جميع رواسم سطح المخروط K.
• قوس قطع مكافئ عندما مستوى الضوء λ يوازي واحد من رواسم K
• قوس قطع زائد عندما λ يوازي اثنين من رواسم K
• نقطة عندما λ يمر بقمة K
• خط عندما λ يلامس سطح K

مثال 1: ظل خط على سطح مخروطي كقطع ناقص

مثال 2: ظل خط على سطح مخروطي كقطع مكافئ

مثال 3: ظل خط على سطح مخروطي كقطع زائد

ظل خط كقطع زائد

 ظل شكل مستوي على سطح مستوي كتقاطع بين سطح ضوء والمستوي

ظل شكل ∆ على سطح α يمكن ان يفسر كتقاطع لسطح ضوء K قاعدتة ذلك الشكل ∆ مع السطح α الذي يتلقى الظل. على سبيل المثال ، يمكن تفسير ظل مثلث كتقاطع بين منشور ثلاثي (triangular prism) والمستوى المتلقي الظل؛ أو تفسير ظل دائرة كتقاطع بين اسطوانة ومستوى. في الأمثلة التالية سوف نعالج بعض الأمثلة للظلال كحالات تقاطع بين كيانات هندسية ، والتي الغرض منها، كما هو الحال في الأمثلة الأخرى لهذا البحث، هو استكشاف مواضيع الهندسة الوصفية والتأكيد على فائدة مفاهيمها المختلفة في ممارسة عقل الطالب-المعماري على التفكير في الفراغ ثلاثي الأبعاد بقواعد واضحة تسمح بتنفيذ العديد من الإنشاءات الهندسية الممكنة لتحقيق النتائج المرجوة.

مثال1 : ظل دائرة ∆ على سطح مستوي يمكن أن يحدد كتقاطع اسطوانة مع مستوى

ظل شكل مستوي على سطح مستوي. ظل دائرة ∆ على سطح مستوي π1 بقصد تنفيذ عملية النمذجة الصلبة ، يمكن تحديد ظل Δ كتقاطع بين اسطوانة الضوء (التي قاعدتها Δ) مع المستوى π1 المتلقي الظل. لتحقيق هذه الغاية، ينبغي إنشاء النموذج الصلب للاسطوانة, ولهذا فهو ضروري تحديد مقطع عرضي قائم لنفس الاسطوانة كما هو مشروح في الخطوات التالية : * يتم تحديد شعاع الضوء C-C* كمحور للنموذج K * يتم وضع مستوى الإنشاء xy بحيث يمر بنقطة من المحور C-C* ومتعامد على نفس المحور. * يتم تحديد الخط u كمحور للتقابل (Affinity) بين المستوى β (للدائرة Δ) مع المستوى α (حيث ينتمي المقطع العرضي Δr). * يتم اختيار من الدائرة Δ , قطرين متزاوجين ومتعامدين مع بعضها البعض (على سبيل المثال 3-4، 5-6) ، وتحديد الخطوط المقابله (3 r-4r, 5r-6r) كأقطار متزاوجة للاهليج ∆r. * بمجرد الانتهاء من تحديد الأقطار المتزاوجة للمقطع العرضي Δr ، يمكن المضي قدما في تنفيذ الانشاء الهندسي المفسر في الشكل -- لإيجاد محاور الاهليج ∆r . * يتم بثق الاهليج Δr ومن ثم قطع اسطوانة الناتجة بالمستويين β وπ1. يمكن ملاحظة نتيجة القطع (في الشكل --) ان الظل Δr , للدائرةΔ, يتطابق مع مقطع الاسطوانة بالمستوى π1

ظل دائرة ∆ على مستوى π1 يحدد كتقاطع بين اسطوانة مع المستوى المتلقي الظل π1 . الدائرة ∆ تمثل قاعدة الاسطوانة K و أشعة الضوء المارة بنقط ∆ تمثل رواسم السطح K.

التقاطع ∆* بين الأسطوانة K مع المستوى π1 من المرجح ان يكون قطع ناقص (اهليج ). لتحديد محاور هذا الاهليج Δ ، ينبغي أن إيجاد قطرين متزاوجان للاهليج * Δ. في ما يلي هناك اجراء يسمح بايجاد محاور الاهليج.

طريقة أخرى لايجاد الظل * Δ ، تكمن في الاستفادة من النمذجة الصلبة لانشاء الاسطوانة ومن ثم قطعها بالمستوى المتلقي الظل. نمذجة الاسطوانة, كما هو الحال في جميع الأسطح الاسقاطية بقمة لانهائية (مثل المنشور والاسطوانة), تتطلب مقطع عرضي قائم ( أي مقطع يحصل علية بمستوى عمودي على محور الاسطوانة) واتجاه البثق (أي اتجاة محور الاسطوانة ). في هذه الحالة ، لتحديد المقطع العرضي Δ r ، ينغي اتباع الاجراء التالي: - تحديد شعاع الضوء C-C* المار بمركز الدائرة كمحور للاسطوانة ؛ - وضع مستوى الانشاء xy بحيث يمر بنقطة من المحور C-C* ويكون عمودي على المحور نفسة ؛ - تحديد محور الاهليج Δ r , باتباع الإجراء السابق (شكل --) . بمجرد انشاء الاهليج Δ r , تنفذ عملية البثق باتجاه المحور . وأخيرا قطع الاسطوانة بالمستوى 1π ، للحصول على ظل الدائرة Δ, وهو المطلوب.

 معلوم قطرين متزاوجين لاهليج المطلوب انشاء هذا الاهليج بواسطة محاورة

معلوم قطرين متزاوجين لاهليج المطلوب انشاء هذا الاهليج بواسطة محاورة

لنفترض أنها حددت مسبقا الأقطار المتزاوجة a' b' لأهليج ∆* ونريد إنشاء هذا الاهليج عن طريق ايجاد محاوره.

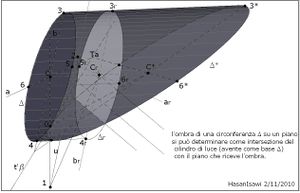
لحل المشكلة نعتبر أن الاهليج ∆’ مسقط لدائرة ∆ من مركز لانهائية وبذلك القطرين a' b' هي مساقط قطرين للدائرة ∆ متعامدة على بعضهما. ووفقا لهذا الاعتبار يمكن استخدام التقابل الافيني (تألف بمركز لانهائي) بين المسقط ∆’ وانقلاب الدائرة ∆ على نفس المستوى حيث يوجد المسقط ∆’. بمتابعة الشكل المرفق يمكن ملاحظة ما يلي:

• محور الانقلاب u يتطابق مع طلع من اطلاع متوازي الاطلاع المحيط الاهليج ∆’. وبهذه الطريقة يمكن تخيل ان الإقطار a b في الفراغ هما ، بالتوالي ، القطر a' موازي لمحور الانقلاب u والقطر b عمودي على نفس u.
• لذلك الانقلاب b* للقطر b ، هو عمودي على المحور u ويمر بالنقطة 0 (نقطة تقاطع b مع المحور)
• والانقلاب d* (قطر المربع المحيط للدائرة ∆) يمر بالنقطة 1 (نقطة التقاء المحور u مع المسقط d' للقطر d)، ويشكل زاوية 45 درجة مع المحور u.
• النقطة C* , التقاء الانقلابين d* e b*, تمثل انقلاب مركز الدائرة ∆.
• الخط الواصل بين النقطتين C* C' ( بالتوالي انقلاب مركز الدائرة ∆ وإسقاط نفس المركز) يحدد اتجاه مركز التألف U ( في هذة الحالة تألف مائل بالنسبة للمحور u ) بين الإسقاط ∆' والانقلاب ∆* للدائرة ∆.
• يعتبر المستقيم C*-C وتر لدائرة مساعدة التي مركزها يقع في النقطة 2 (نقطة تقاطع u مع منصف المستقيم C*-C) ونصف قطرها يساوي المستقيم 2-C* (او 2-C').
• محيط الدائرة المساعدة يمر بالمراكز C* و C' ويتقاطع مع المحور u في النقاط 3 و 4. ووفقاً للخاصية الهندسية للدائرة ، بوصل النقاط 3 و 4 (التي تنتمي إلى قطر الدائرة المساعدة) مع المراكز C* e C' ' (التي تنتمي الى محيط الدائرة المساعدة) ، حصلنا على زوجين من الخطوط e*,f* و e',f' التي تشكل فيما بينها، اثنين اثنين, زوايا قائمة. وبالتالي فقد حصلنا على المحاور المطلوبة e',f’ للاهليج ∆'
• ومنذ أن النقاط المتقابلة (مثل 8 * و 8 ') تنتمي إلى خطوط متقابلة (f* و f') وتستطف باتجاه مركز التقابل U ، فان الأطراف 5', 6', 7' و8 للمحاور e' ,f' تحدد كتقاطع بين المحاور e' ,f’ مع الخطوط المتوازية لاتجاة U والمارة بالنقاط 5*, 6*, 7* 8*.

 نتائج

قد يكون على حق, جزئياً ، من يقول ان إنشاء ظلال النماذج الافتراضية يتم تلقائيا ، وأنة كافي معرفة القليل من قواعد الهندسة الوصفية للحصول على نتائج اظهار مقنعة. ولكن يجب أن يكزن لدينا رؤية أوسع للاقتناع بحقائق أخرى. ينبغي أن نتذكر دائما الغرض الرئيسي من تدريس الهندسة الوصفية ، متجاوزون تلك التقنيات الهادفة إلى حل مشكلة هندسية معينة, ألا وهو ممارسة العقل على إدراك الفراغ والسيطرة بشكل دقيق على أشكاله الممكنة وأساليب اظهارة المختلفة. وبما ان فكرة التصميم تنبع في المقام الأول من خبرة وتجربة العقل ، فان تدريس الهندسة الوصفية يجد ما يبرره اذا كان الهدف هو تدريب هذا العقل على التفكير في كيفية عرض فكرة تصميمية معينة والتحقق من ميزاتها الهندسية والإدراكية. وعلاوة على ذلك ، وبالاتفاق مع من يقول أن الصورة تساوي ألف كلمة ، أود أن أؤكد على أن إنشاء تلك الصورة كان قد مر بمراحل من التفكير والمناقشة مليئة بالآلاف من الكلمات. وبهذا أريد ان ا قول إن هناك حاجة ماسة الى معرفة اللغة الخاصة بالهندسة الوصفية لتنظيم ومناقشة العديد من الشكوك التي عادة ما تتشكل عند انشاء وإظهار الأشكال الهندسية المختلفة وتكويناتها أللانهائية.

ولكي أكون أكثر قناعة ، على الأقل بالنسبة لأولئك المتشككين بفائدة الهندسة الوصفية، أود التأكيد ان مفاهيم وطريقة عمل الهندسة الوصفية ، تسمح من الناحية التقنية بتنفيذ الإنشاءات الهندسية المختلفة في مراحل إعداد عمليات توليد النماذج ثلاثية الأبعاد ومن ثم في تعيين أساليب الاطهار المناسبة.

 طالع أيضاً

• Problemi di incidenza
• problemi di misura
• problemi di reciproche posizioni

 وصلات خارجية

• الرسم والاظهار المعماري
• Geometria Descrittiva