مركز الجاذبية

مركز الجاذبية والاستقرار. لإيجاد مركز الجاذبية لجسم مسطح، يعلق الجسم وثقل الفادن من نقطة واحدة. ويرسم خط على طول خيط الفادن. وتكرر العملية من نقطة أخرى، فيكون مركز الجاذبية حيث يلتقي الخطان. ولا يستقر الجسم إذا وقع خيط الفادن خارج قاعدة الجسم.

مركز الجاذبية Center of gravity النقطة في الجسم حيث تعمل قوة الجاذبية. فإذا علّق جسم من أي نقطة على الخط الرأسي المار بمركز جاذبيته، فإن الجسم يظل ساكنا. أما إذا كان مركز الجاذبية على جانب من نقطة يمكن للجسم أن يدور حولها، فإن الجسم سيتحول نحو ذلك الاتجاه.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 تعريف

The center of mass $\mathbf {R}$ of a system of particles is defined as the average of their positions, $\mathbf {r} _{i}$, weighted by their masses, $m_{i}$:

$\mathbf {R} ={\sum m_{i}\mathbf {r} _{i} \over \sum m_{i}}.$

For a continuous distribution with mass density $\rho (\mathbf {r} )$ and total mass $M$, the sum becomes an integral:

$\mathbf {R} ={\frac {1}{M}}\int \mathbf {r} \;dm={\frac {1}{M}}\int \rho (\mathbf {r} )\,\mathbf {r} \ dV={\frac {\int \rho (\mathbf {r} )\,\mathbf {r} \ dV}{\int \rho (\mathbf {r} )\ dV}}.$

ويقع مركز جاذبية أرجوحة (نوّاسة) طفل في وسط اللوح عندما لا يجلس عليه أحد. وإذا دارت الأرجوحة حول وسطها فسوف تبقى متوازنة. وعندما يصعد طفلان مختلفا الوزن على الطرفين المتضادين للأرجوحة فستكون قوة الجاذبية أكبر في أحد الطرفين. وسوف يكون مركز الجاذبية في هذه الحالة بين مركز اللوح والنهاية التي عليها الثقل الأكبر، حيث يجلس الطفل الأثقل وزنًا. وسوف تميل الأرجوحة تجاه هذه النهاية. وإذا ما تحرك الطفل الأثقل وزنًا نحو وسط الأرجوحة فسوف يتحرك مركز الجاذبية أيضا تجاه وسط اللوح وسوف يتوازن ثانية.

وتعمل قوة الجاذبية في جميع نقاط الجسم حيث تكون هناك كتلة (مادة) وليس في مركز الجاذبية فقط. ويوضح علماء الفيزياء كيف تعمل الجاذبية في الأجسام من خلال تغيير العزم. والعزم هو مقياس تحوّل القوة. وعزم قوة الجاذبية المؤثرة في أية نقطة يعرف بحاصل ضرب القوة في المسافة الأفقية لنقطة المركز المستخدمة. وللعزم حجم واتجاه، ذلك أن عزوم القوة المؤثرة في جانب من الأرجوحة تعمل على تحريكها إلى أعلى أو إلى أسفل. والعزم الفاعل في الجانب المضاد يعمل على تحويلها للاتجاه العكسي. والعزمان اللذان لهما حجم واحد واتجاهان مختلفان يلغي كل منهما الآخر. وعلى هذا فإن الأرجوحة لا تتحرك. ولذلك وبالقياس للعزم، فإن مركز الجاذبية لأي جسم، هو النقطة حيث تلغي عزوم قوى الجاذبية بعضها بعضًا. ومركز الجاذبية في الأرجوحة هو وسط اللوح لأن العزوم يلغي كل منها الآخر هناك.

وعندما يتمركز الجسم بحيث لا يتوازن، فإنه يدور حتى يصل مركز جاذبيته إلى الاتزان المستقر (أقل وضع ممكن). وإذا توازن الجسم مع مركز جاذبية مباشرة فوق المركز، فإن أي حركة سوف تتسبب في عدم استقرار الجسم. ويقال عن توازن الجسم بهذه الطريقة أنه في وضع اتزان غير مستقر.

وعندما يتحرك الجسم، فإن مركز الجاذبية يتحرك كما لو كانت كل كتلة الجسم مركزة هناك. وحركة الجسم التي تنشأ بتأثير قوة الجاذبية توصف بأنها مجموع حركة مركز جاذبية الجسم ودوران الجسم حول مركز جاذبيته. ويكون مركز كتلة الجسم في النقطة نفسها مركزًا للجاذبية. ويستخدم مركز الكتلة لحساب حركة الأجسام بالنسبة لكل أنواع القوة وليس فقط قوة الجاذبية.

 تناوب المراكز الجماعية

Diagram of an educational toy that balances on a point: the CM (C) settles below its support (P). Any object whose CM is below the fulcrum will not topple.

The suspending chair trick makes use of the human body's center of mass, and the fact that it's surprisingly high.

Motion of Barycenter of solar system relative to the Sun.

 يبين الجدول التالي بعض الأمثلة من وجهة نظرنا النظام الشمسي

Examples

Larger body	m1 (mE=1)	Smaller body	m2 (mE=1)	a (km)	r1 (km)	R1 (km)	r1/R1
Remarks
Earth	1	Moon	0.0123	384,000	4,670	6,380	0.732
The Earth has a perceptible "wobble".
Pluto	0.0021	Charon	0.000254 (0.121 mPluto)	19,600	2,110	1,150	1.83
Both bodies have distinct orbits around the barycenter, and as such Pluto and Charon were considered as a double planet by many before the redefinition of planet in August 2006.
Sun	333,000	Earth	1	150,000,000 (1 AU)	449	696,000	0.000646
The Sun's wobble is barely perceptible.
Sun	333,000	Jupiter	318 (0.000955 mSun)	778,000,000 (5.20 AU)	742,000	696,000	1.07
The Sun orbits a barycenter just above its surface.

 الرسوم المتحركة

Two bodies of similar mass orbiting around a common barycenter. (similar to the 90 Antiope system)	Two bodies with a difference in mass orbiting around a common barycenter, as in the Pluto-Charon system.	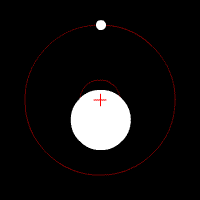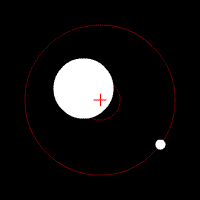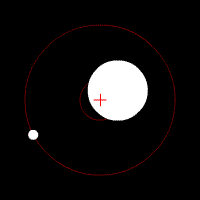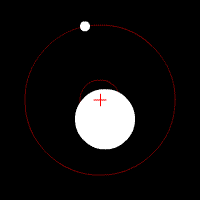Two bodies with a major difference in mass orbiting around a common barycenter (similar to the Earth-Moon system)	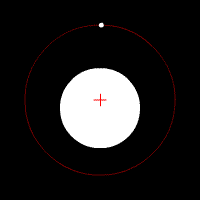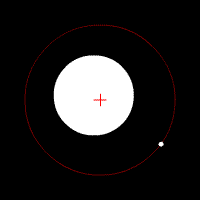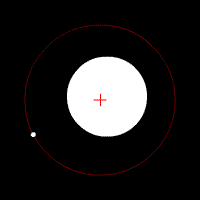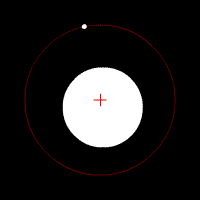Two bodies with an extreme difference in mass orbiting around a common barycenter (similar to the Sun-Earth system)
Two bodies with similar mass orbiting around a common barycenter with elliptic orbits (a common situation for binary stars)

 تحديد موقع مركز الجاذبية(مركز الثقل)

Step 1: An arbitrary 2D shape.	Step 2: Suspend the shape from a location near an edge. Drop a plumb line and mark on the object.	Step 3: Suspend the shape from another location not too close to the first. Drop a plumb line again and mark. The intersection of the two lines is the center of mass.

[Image:COG 2.png]] ${\frac {3\times -\pi 2.5^{2}+5\times 10^{2}+13.33\times {\frac {10^{2}}{2}}}{-\pi 2.5^{2}+10^{2}+{\frac {10^{2}}{2}}}}\approx 8.5$ units.

 أنظر أيضاً

• Center of gravity of an aircraft
• Center of percussion
• Center of pressure
• Metacentric height
• Roll center
• Two-body problem
• Weight distribution

 المصادر

• الموسوعة المعرفية الشاملة

• Feynman, Richard (1963). The Feynman Lectures on Physics. Addison Wesley. ISBN 0-201-02116-1. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Goldstein, Herbert (2002). Classical Mechanics (3e ed.). Addison Wesley. ISBN 0-201-65702-3. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Kleppner, Daniel (1973). An Introduction to Mechanics (2e ed.). McGraw-Hill. ISBN 0-07-035048-5. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Marion, Jerry (1995). Classical Dynamics of Particles and Systems (4e ed.). Harcourt. ISBN 0-03-097302-3. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Murray, Carl (1999). Solar System Dynamics. Cambridge UP. ISBN 0-521-57295-9. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Symon, Keithe R. (1971). Mechanics (3rd edition ed.). Addison-Wesley. ISBN 0-201-07392-7. {{cite book}}: |edition= has extra text (help)
• Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 وصلات خارجية

ابحث عن barycentre في
قاموس المعرفة.

• Centre of mass model - A Background model for segmentation of moving objects in image processing.
• barycenter fold by Paul Niquette.
• Center of Gravity Encyclopaedia Britannica.
• Locating the center of mass by mechanical means.
• The dynamic centre of gravity Engineer Xavier Borg - Blaze Labs Research
• Measuring Center of Gravity Space Electronics, manufacturer of center of gravity measurement instruments.
• Motion of the Center of Mass shows that the motion of the center of mass of an object in free fall is the same as the motion of a point object.
• The solar system's barycenter Simulations showing the effect each planet contributes to the solar system's barycenter
• Polygon Center of Mass An algorithm that would calculate the center of mass of a polygonal figure consisting of n points (x, y).