قوانين كپلر للحركة الكوكبية

قوانين كپلر للحركة الكوكبية أثبت العالم الفلكي يوهانس كپلر أن النظام الذي وضعه كوپرنيكس عن مركزية الشمس هو الوحيد الذي يعكس الحقيقة بدقة .
وعن طريق عمليات حسابية معقدة و متعددة ، وضع كبلر القوانين الثلاثة الهامة فيما يتعلق بحركة الكواكب . وهذه القوانين هي:
- تدور الكواكب حول الشمس بحركة ليست دائرية و لكن في قطع ناقص تحتل الشمس إحدى بؤرتيه و القطع الناقص هو الشكل الذي نحصل عليه اذا قطعنا جسماً اسطوانياً بمنشار مائل .
- تختلف سرعة الكوكب في دورانه حول الشمس تبعاً لبعده عنها ، فإذا كان قريباً ، فإنه يدور بسرعة أكبر ، وكلما زاد بعده كلما قلت سرعته في الدوران ، حيث تتساوى مساحة المثلثين المشكلين فيما بين الشمس و قوس المسافات المغطاة من كوكبين في نفس الوقت .
- النسبة بين مربعي فترتي دوران أي كوكبين هي نفسها النسبة بين القيمة التكعبية للبعد المتوسط لكل منهما عن الشمس و مثال علي ذلك :
يستغرق الكوكب عطارد 88 يوماً و الأرض 365 في مدارهما مرة واحدة حول الشمس ، فإذا ما ضربنا كلا الرقمين بنفسه للحصول على مربعهما نحصل على 7744 ، 133225 . ويبلغ الرقم الرقم الثاني حوالي 17 مثل للأول . و لننتقل الآن إلى نسبة بعدهما عن الشمس . فبعد عطارد في المتوسط حوالي 36 مليون ميل عن الشمس أما الأرض فتبعد حوالي 93 مليون ميل في المتوسط . واذا ما ضربنا الارقام بنفسهما مرتين للحصول على القيمة التكعيبية لهما نحصل على 46656 ، 804357 . وهنا نجد أن النسبة بين هذين الرقمين قريبة جداً من النسبة الأولى اي 17:1 .
هذه القوانين لاتزال اساسية حتى يومنا هذا و تعتبر خطوة كبيرة إلى الامام في المعرفة البشرية
المكان كدالة في الزمن
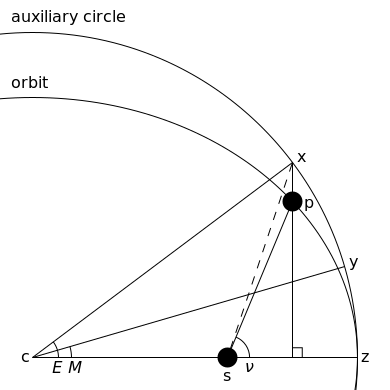
The Keplerian problem assumes an elliptical orbit and the four points:
- s the sun (at one focus of ellipse);
- z the perihelion
- c the center of the ellipse
- p the planet
and
- distance from center to perihelion, the semimajor axis,
- the eccentricity,
- the semiminor axis,
- the distance from sun to planet.
and the angle
- the planet as seen from the sun, the true anomaly.
المصادر
انظر أيضاً
وصلات خارجية
- Crowell, Benjamin, Conservation Laws, http://www.lightandmatter.com/area1book2.html, an online book that gives a proof of the first law without the use of calculus. (see section 5.2, p.112)
- David McNamara and Gianfranco Vidali, Kepler's Second Law -JAVA Interactive Tutorial, http://www.phy.syr.edu/courses/java/mc_html/kepler.html, an interactive JAVA applet that aids in the understanding of Kepler's Second Law.
- University of Tennessee's Dept. Physics & Astronomy: Astronomy 161 page on Johannes Kepler: The Laws of Planetary Motion [1]
- Equant compared to Kepler: interactive model [2]
- Kepler's Third Law:interactive model[3]