غزّال
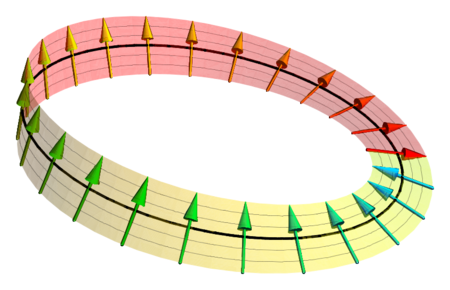
A spinor visualized as a vector pointing along the Möbius band, exhibiting a sign inversion when the circle (the "physical system") is continuously rotated through a full turn of 360°.[أ]
في الرياضيات والفيزياء، غـزّال أو سپينور (Spinor ؛ /spɪnər/) هم عناصر فضاء متجهات من مركـَّبة التي يمكن أن تقترن بالفضاء الاقليدي.[ب] وبشكل أكثر تحديداً ضمن نظرية المجموعات المتعامدة على كائنات رياضية مشابهة للأشعة أو المتجهات لكنها تغير اشارتها بعد تطبيق دوران بقيمة عليها أي دائرة كاملة.
مقدمة
A gradual rotation can be visualized as a ribbon in space.[ت] Two gradual rotations with different classes, one through 360° and one through 720° are illustrated here in the belt trick puzzle. A solution of the puzzle is a continuous manipulation of the belt, fixing the endpoints, that untwists it. This is impossible with the 360° rotation, but possible with the 720° rotation. A solution, shown in the second animation, gives an explicit homotopy in the rotation group between the 720° rotation and the 0° identity rotation.
الملخص في أبعاد قليلة
- In 1 dimension (a trivial example), the single spinor representation is formally Majorana, a real 1-dimensional representation that does not transform.
- In 2 Euclidean dimensions, the left-handed and the right-handed Weyl spinor are 1-component complex representations, i.e. complex numbers that get multiplied by e±iφ/2 under a rotation by angle φ.
- In 3 Euclidean dimensions, the single spinor representation is 2-dimensional and quaternionic. The existence of spinors in 3 dimensions follows from the isomorphism of the groups SU(2) ≅ Spin(3) that allows us to define the action of Spin(3) on a complex 2-component column (a spinor); the generators of SU(2) can be written as Pauli matrices.
- In 4 Euclidean dimensions, the corresponding isomorphism is Spin(4) ≅ SU(2) × SU(2). There are two inequivalent quaternionic 2-component Weyl spinors and each of them transforms under one of the SU(2) factors only.
- In 5 Euclidean dimensions, the relevant isomorphism is Spin(5) ≅ USp(4) ≅ Sp(2) that implies that the single spinor representation is 4-dimensional and quaternionic.
- In 6 Euclidean dimensions, the isomorphism Spin(6) ≅ SU(4) guarantees that there are two 4-dimensional complex Weyl representations that are complex conjugates of one another.
- In 7 Euclidean dimensions, the single spinor representation is 8-dimensional and real; no isomorphisms to a Lie algebra from another series (A or C) exist from this dimension on.
- In 8 Euclidean dimensions, there are two Weyl–Majorana real 8-dimensional representations that are related to the 8-dimensional real vector representation by a special property of Spin(8) called triality.
- In d + 8 dimensions, the number of distinct irreducible spinor representations and their reality (whether they are real, pseudoreal, or complex) mimics the structure in d dimensions, but their dimensions are 16 times larger; this allows one to understand all remaining cases. See Bott periodicity.
- In spacetimes with p spatial and q time-like directions, the dimensions viewed as dimensions over the complex numbers coincide with the case of the (p + q)-dimensional Euclidean space, but the reality projections mimic the structure in |p − q| Euclidean dimensions. For example, in 3 + 1 dimensions there are two non-equivalent Weyl complex (like in 2 dimensions) 2-component (like in 4 dimensions) spinors, which follows from the isomorphism SL(2, ℂ) ≅ Spin(3,1).
| Metric signature | Weyl, complex | Conjugacy | Dirac, complex |
Majorana–Weyl, real | Majorana, real | ||
|---|---|---|---|---|---|---|---|
| Left-handed | Right-handed | Left-handed | Right-handed | ||||
| (2,0) | 1 | 1 | Mutual | 2 | – | – | 2 |
| (1,1) | 1 | 1 | Self | 2 | 1 | 1 | 2 |
| (3,0) | – | – | – | 2 | – | – | – |
| (2,1) | – | – | – | 2 | – | – | 2 |
| (4,0) | 2 | 2 | Self | 4 | – | – | – |
| (3,1) | 2 | 2 | Mutual | 4 | – | – | 4 |
| (5,0) | – | – | – | 4 | – | – | – |
| (4,1) | – | – | – | 4 | – | – | – |
| (6,0) | 4 | 4 | Mutual | 8 | – | – | 8 |
| (5,1) | 4 | 4 | Self | 8 | – | – | – |
| (7,0) | – | – | – | 8 | – | – | 8 |
| (6,1) | – | – | – | 8 | – | – | – |
| (8,0) | 8 | 8 | Self | 16 | 8 | 8 | 16 |
| (7,1) | 8 | 8 | Mutual | 16 | – | – | 16 |
| (9,0) | – | – | – | 16 | – | – | 16 |
| (8,1) | – | – | – | 16 | – | – | 16 |
انظر أيضاً
ملاحظات
- ^ Spinors in three dimensions are points of a line bundle over a conic in the projective plane. In this picture, which is associated to spinors of a three-dimensional pseudo-Euclidean space of signature (1,2), the conic is an ordinary real conic (here the circle), the line bundle is the Möbius bundle, and the spin group is SL2(ℝ). In Euclidean signature, the projective plane, conic and line bundle are over the complex instead, and this picture is just a real slice.
- ^ Spinors can always be defined over the complex numbers. However, in some signatures there exist real spinors. Details can be found in spin representation.
- ^ The TNB frame of the ribbon defines a rotation continuously for each value of the arc length parameter.
الهامش
الكلمات الدالة: