خماسي عشري

Regular pentadecagon
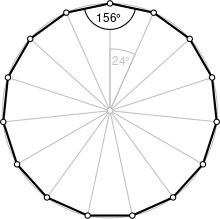A regular pentadecagon
النوع	مضلع منتظم
الأضلاع والرؤوس	{{{p15 جانب}}}
رمز شلفلي	{{{p15-شلفلي}}}
مخططات كوكستر-دنكن
مجموعة التماثل	Dihedral (D15), order 2×15
الزاوية الداخلية (الدرجات)	156°
الخصائص	Convex, cyclic, equilateral, isogonal, isotoxal

في الهندسة الرياضية، الخماسي عشري pentadecagon هو مضلع له 15 ضلع و 15 زاوية.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 خماسي عشري منتظم

• في الخماسي عشري المنتظم قياس الزاوية الداخلية يساوي 156°.
• مساحة خماسي عشري منتظم له طول ضلع a تعطى بالعلاقة:

${\begin{aligned}A&={\frac {15}{4}}a^{2}\cot {\frac {\pi }{15}}\\&={\frac {15a^{2}}{8}}\left({\sqrt {3}}+{\sqrt {15}}+{\sqrt {2}}{\sqrt {5+{\sqrt {5}}}}\right)\\&\simeq 17.6424\,a^{2}.\end{aligned}}$

 الإنشاء

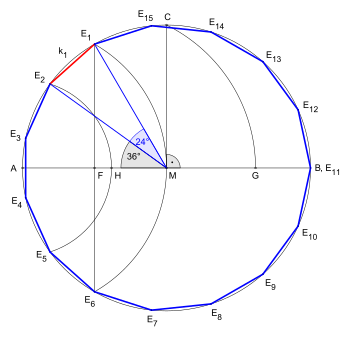
As 15 = 3 × 5, a product of distinct Fermat primes, a regular pentadecagon is constructible using compass and straightedge: The following constructions of regular pentadecagons with given circumcircle are similar to the illustration of the proposition XVI in Book IV of Euclid's Elements.

Compare the construction according Euclid in this image: Pentadecagon

In the construction for given circumcircle: ${\overline {FG}}={\overline {CF}}{\text{,}}\;{\overline {AH}}={\overline {GM}}{\text{,}}\;|E_{1}E_{6}|$ is a side of equilateral triangle and $|E_{2}E_{5}|$ is a side of a regular pentagon. The point $H$ divides the radius ${\overline {AM}}$ in golden ratio: ${\frac {\overline {AH}}{\overline {HM}}}={\frac {\overline {AM}}{\overline {AH}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1.618{\text{.}}$

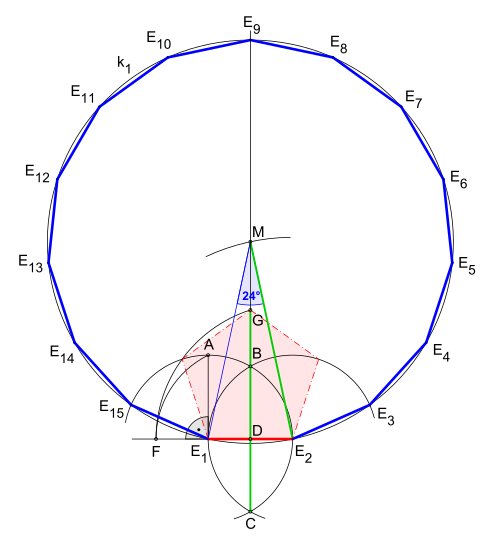
Compared with the first animation (with green lines) are in the following two images the two circular arcs (for angles 36° and 24°) rotated 90° counterclockwise shown. They do not use the segment ${\overline {CG}}$, but rather they use segment ${\overline {MG}}$ as radius ${\overline {AH}}$ for the second circular arc (angle 36°).

A compass and straightedge construction for a given side length. The construction is nearly equal to that of the pentagon at a given side, then also the presentation is succeed by extension one side and it generates a segment, here ${\overline {FE_{2}}}{\text{,}}$ which is divided according to the golden ratio:

${\frac {\overline {E_{1}E_{2}}}{\overline {E_{1}F}}}={\frac {\overline {E_{2}F}}{\overline {E_{1}E_{2}}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1.618{\text{.}}$

Circumradius ${\overline {E_{2}M}}=R\;;\;\;$ Side length ${\overline {E_{1}E_{2}}}=a\;;\;\;$ Angle $DE_{1}M=ME_{2}D=78^{\circ }$

${\begin{aligned}R&=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)={\frac {1}{2}}\cdot {\sqrt {8+2\cdot {\sqrt {5}}+2{\sqrt {15+6\cdot {\sqrt {5}}}}}}\cdot a\\&={\frac {\sin(78^{\circ })}{\sin(24^{\circ })}}\cdot a\approx 2.40486\cdot a\end{aligned}}$

Construction for a given side length

Construction for a given side length as animation

 التماثل

The symmetries of a regular pentadecagon as shown with colors on edges and vertices. Lines of reflections are blue. Gyrations are given as numbers in the center. Vertices are colored by their symmetry positions.

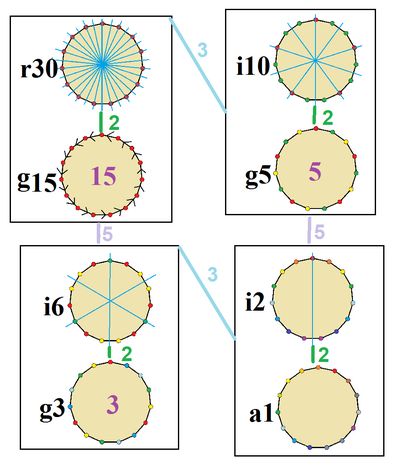
The regular pentadecagon has Dih₁₅ dihedral symmetry, order 30, represented by 15 lines of reflection. Dih₁₅ has 3 dihedral subgroups: Dih₅, Dih₃, and Dih₁. And four more cyclic symmetries: Z₁₅, Z₅, Z₃, and Z₁, with Z_n representing π/n radian rotational symmetry.

On the pentadecagon, there are 8 distinct symmetries. John Conway labels these symmetries with a letter and order of the symmetry follows the letter. He gives r30 for the full reflective symmetry, Dih₁₅. He gives d (diagonal) with reflection lines through vertices, p with reflection lines through edges (perpendicular), and for the odd-sided pentadecagon i with mirror lines through both vertices and edges, and g for cyclic symmetry. a1 labels no symmetry.

These lower symmetries allows degrees of freedoms in defining irregular pentadecagons. Only the g15 subgroup has no degrees of freedom but can seen as directed edges.

 النجوم الخمس عشارية

There are three regular star polygons: {15/2}, {15/4}, {15/7}, constructed from the same 15 vertices of a regular pentadecagon, but connected by skipping every second, fourth, or seventh vertex respectively.

There are also three regular star figures: {15/3}, {15/5}, {15/6}, the first being a compound of three pentagons, the second a compound of five equilateral triangles, and the third a compound of ثلاث نجوم خماسية.

الشكل المركب {15/3} يمكن رؤيته بشكل فضفاض كمكافئ ثنائي الأبعاد لمركب من خمس رباعيات الأسطح ثلاثي الأبعاد.

الصورة	{15/2}	{15/3} or 3{5}	{15/4}	{15/5} or 5{3}	{15/6} or 3{5/2}	{15/7}
الزاوية الداخلية	132°	108°	84°	60°	36°	12°

 Isogonal pentadecagons

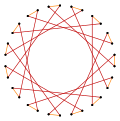
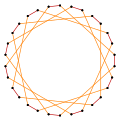
Deeper truncations of the regular pentadecagon and pentadecagrams can produce isogonal (vertex-transitive) intermediate star polygon forms with equal spaced vertices and two edge lengths.

Vertex-transitive truncations of the pentadecagon
Quasiregular	Isogonal							Quasiregular
t{15/2}={30/2}								t{15/13}={30/13}
t{15/7} = {30/7}								t{15/8}={30/8}
t{15/11}={30/22}								t{15/4}={30/4}

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مضلعات پتري

The regular pentadecagon is the Petrie polygon for some higher-dimensional polytopes, projected in a skew orthogonal projection:

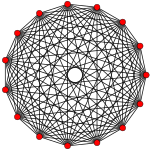14-simplex (14D)

 الاستخدامات

A regular triangle, decagon, and pentadecagon can completely fill a plane vertex. However, due to the triangle's odd number of sides, the figures cannot alternate around the triangle, so the vertex cannot produce a semiregular tiling.

 انظر أيضاً

• Construction of the pentadecagon at given side length, calculation of the circumradius $R$ (German)
• Construction of the pentadecagon at given side length, exemplification: circumradius ${\overline {CG}}=R$

 وصلات خارجية

• Eric W. Weisstein, Pentadecagon at MathWorld.