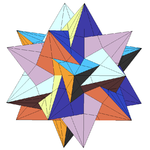
مركب من خمس رباعيات الأسطح

Compound of five tetrahedra
Type	Regular compound
Coxeter symbol	{5,3}[5{3,3}] {3,5}
Index	UC5, W24
Elements (As a compound)	5 tetrahedra: F = 20, E = 30, V = 20
Dual compound	Self-dual
Symmetry group	chiral icosahedral (I)
Subgroup restricting to one constituent	chiral tetrahedral (T)

3D model of a compound of five tetrahedra

The compound of five tetrahedra is one of the five regular polyhedral compounds. This compound polyhedron is also a stellation of the regular icosahedron. It was first described by Edmund Hess in 1876.

It can be seen as a faceting of a regular dodecahedron.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 كمركب

It can be constructed by arranging five tetrahedra in rotational icosahedral symmetry (I), as colored in the upper right model. It is one of five regular compounds which can be constructed from identical Platonic solids.

It shares the same vertex arrangement as a regular dodecahedron.

There are two enantiomorphous forms (the same figure but having opposite chirality) of this compound polyhedron. Both forms together create the reflection symmetric compound of ten tetrahedra.

It has a density of higher than 1.

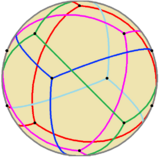As a spherical tiling

Transparent Models (Animation)

Five interlocked tetrahedra

 كتنجم

It can also be obtained by stellating the icosahedron, and is given as Wenninger model index 24.

مخطط التنجم	لب التنجم	Convex hull
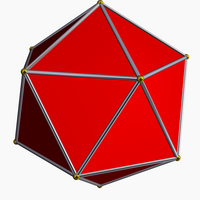	Icosahedron	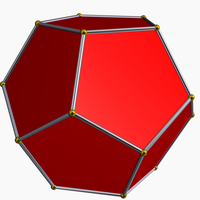Dodecahedron

 As a facetting

Five tetrahedra in a dodecahedron.

It is a faceting of a dodecahedron, as shown at left.

 نظرية المجموعات

The compound of five tetrahedra is a geometric illustration of the notion of orbits and stabilizers, as follows.

The symmetry group of the compound is the (rotational) icosahedral group I of order 60, while the stabilizer of a single chosen tetrahedron is the (rotational) tetrahedral group T of order 12, and the orbit space I/T (of order 60/12 = 5) is naturally identified with the 5 tetrahedra – the coset gT corresponds to which tetrahedron g sends the chosen tetrahedron to.

 خاصية ثنائية غير معتادة

Compound of five tetrahedra

This compound is unusual, in that the dual figure is the enantiomorph of the original. If the faces are twisted to the right, then the vertices are twisted to the left. When we dualise, the faces dualise to right-twisted vertices and the vertices dualise to left-twisted faces, giving the chiral twin. Figures with this property are extremely rare.

 انظر أيضاً

• Compound of ten tetrahedra
• Compound of five cubes

 المراجع

• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
• H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 The five regular compounds, pp.47-50, 6.2 Stellating the Platonic solids, pp.96-104
• Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The Fifty-Nine Icosahedra (3rd ed.). Tarquin. ISBN 978-1-899618-32-3. MR 0676126. (1st Edn University of Toronto (1938))

 وصلات خارجية

• Eric W. Weisstein, Tetrahedron 5-Compound at MathWorld.
• Metal Sculpture of Five Tetrahedra Compound
• VRML model: [1]
• Compounds of 5 and 10 Tetrahedra by Sándor Kabai, The Wolfram Demonstrations Project.
• قالب:KlitzingPolytopes

Notable stellations of the icosahedron
Regular	Uniform duals			Regular compounds			Regular star	Others
(Convex) icosahedron	Small triambic icosahedron	Medial triambic icosahedron	Great triambic icosahedron	Compound of five octahedra	Compound of five tetrahedra	Compound of ten tetrahedra	Great icosahedron	Excavated dodecahedron	Final stellation
The stellation process on the icosahedron creates a number of related polyhedra and مركبات بتماثل عشريني الأوجه.