موتر

لاحظ أنه في الاستخدام الشائع، التعبير تنسور tensor يُستخدم أيضاً ليشير إلى حقل موتر.

الاجهاد، موتر من الدرجة الثانية. مكونات الموتر، في نظام احداثيات كارتيزية ثلاثي الأبعاد، يشكل المصفوفة

\scriptstyle \sigma ={\begin{bmatrix}\mathbf {T} ^{(\mathbf {e} _{1})}\\\mathbf {T} ^{(\mathbf {e} _{2})}\\\mathbf {T} ^{(\mathbf {e} _{3})}\\\end{bmatrix}}={\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}

التي صفوفها هي القوى العاملة على الأوجه

\mathbf {e} _{1}

،

\mathbf {e} _{2}

، و

\mathbf {e} _{3}

للمكعب.

المُوَتِّر^[1] أو المُمْتَدّ^[2] إنگليزية: tensor هو، في الرياضيات، أحد الدالات الرياضية بجانب الأعداد أو الكميات المطلقة generalized 'quantity' التي لا تتميز بوحدات للقياس. يتميز الموتّر بأنه يحتوي في خواصه خواص الأعداد المطلقة scalar، والمتجهات vectors، والمعاملات الخطية linear operator.

يمكن للموتّر أن يكتب بدلالة الإحداثيات، أو كمنظومة أعداد مطلقة arrays of scalars، لكنه يعرف على أنه مستقل عن أي إطار مرجعي frame of reference.

في الرياضيات ، التينسور هو أحد أنواع الكائنات الهندسية أو لنقل انه كمية معممة generalized 'quantity' . مصطلح التينسور يحوي ضمنه مفهوم القياسي scalar ، المتجهات vectors ، و المعاملات الخطية linear operator .

يمكن للتينسور أن يكتب بدلالة جمل إحداثية ، كمنظومة قياسيات arrays of scalars لكنه يعرف على أنه مستقل عن أي جملة مرجعية أو إطار مرجعي frame of reference .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

التعريف

كمصفوفات متعددة الأبعاد

$B_{i}C^{i}=B_{1}C^{1}+B_{2}C^{2}+\cdots B_{n}C^{n}$ </ref> The components vⁱ of a column vector v transform with the inverse of the matrix R,

{\hat {v}}^{i}=(R^{-1})_{j}^{i}v^{j},

where the hat denotes the components in the new basis. This is called a contravariant transformation law, because the vector transforms by the inverse of the change of basis. In contrast, the components, w_i, of a covector (or row vector), w transform with the matrix R itself,

{\hat {w}}_{i}=R_{i}^{j}w_{j}.

This is called a covariant transformation law, because the covector transforms by the same matrix as the change of basis matrix. The components of a more general tensor transform by some combination of covariant and contravariant transformations, with one transformation law for each index. If the transformation matrix of an index is the inverse matrix of the basis transformation, then the index is called contravariant and is traditionally denoted with an upper index (superscript). If the transformation matrix of an index is the basis transformation itself, then the index is called covariant and is denoted with a lower index (subscript).

The transformation law for an order p + q tensor with p contravariant indices and q covariant indices is thus given as,

{\hat {T}}_{j'_{1},\ldots ,j'_{q}}^{i'_{1},\ldots ,i'_{p}}=(R^{-1})_{i_{1}}^{i'_{1}}\cdots (R^{-1})_{i_{p}}^{i'_{p}}R_{j'_{1}}^{j_{1}}\cdots R_{j'_{q}}^{j_{q}}T_{j_{1},\ldots ,j_{q}}^{i_{1},\ldots ,i_{p}}.

Here the primed indices denote components in the new coordinates, and the unprimed indices denote the components in the old coordinates. Such a tensor is said to be of order or type (p, q). The terms "order", "type", "rank", "valence", and "degree" are all sometimes used for the same concept. Here, the term "order" or "total order" will be used for the total dimension of the array (or its generalisation in other definitions), p+q in the preceding example, and the term "type" for the pair giving the number contravariant and covariant indices. A tensor of type (p, q) is also called as a (p, q)-tensor for short.

As an example, the matrix of a linear transformation in a basis is a rectangular array $T$ that transforms under a change of basis R by ${\hat {T}}=R^{-1}TR$ . In terms of the individual matrix entries, this transformation law has the form

{\hat {T}}_{i'_{2}}^{i'_{1}}=(R^{-1})_{i_{1}}^{i'_{1}}T_{i_{2}}^{i_{1}}R_{i'_{2}}^{i_{2}}

so the tensor corresponding to the matrix of a linear transformation has one covariant and one contravariant index: it has type (1,1). A linear transformation itself does not actually depend on a basis: it is just a linear map that accepts a vector as an argument and produces another vector. The transformation law for the matrix of a linear transformation is consistent with the transformation law for a contravariant vector, so that the action of a linear transformation on a contravariant vector is represented in coordinates as the matrix product of their respective coordinate representations. That is, the components $(Tv)^{i}$ are given by $(Tv)^{i}=T_{j}^{i}v^{j}$ . These components transform contravariantly, since

({\widehat {Tv}})^{i'}={\hat {T}}_{j'}^{i'}{\hat {v}}^{j'}=\left[(R^{-1})_{i}^{i'}T_{j}^{i}R_{j'}^{j}\right]\left[(R^{-1})_{j}^{j'}v^{j})\right]=(R^{-1})_{i}^{i'}(Tv)^{i}.

This discussion motivates the following formal definition:^[3]

Definition. A tensor of type (p, q) is an assignment of a multidimensional array
$T_{j_{1}\dots j_{q}}^{i_{1}\dots i_{p}}[\mathbf {f} ]$

to each basis $f = (e 1,..., e n)$ of a fixed n-dimensional vector space such that, if we apply the change of basis

$\mathbf {f} \mapsto \mathbf {f} \cdot R=\left(R_{1}^{i}\mathbf {e} _{i},\dots ,R_{n}^{i}\mathbf {e} _{i}\right)$

then the multidimensional array obeys the transformation law

$T_{j'_{1}\dots j'_{q}}^{i'_{1}\dots i'_{p}}[\mathbf {f} \cdot R]=(R^{-1})_{i_{1}}^{i'_{1}}\cdots (R^{-1})_{i_{p}}^{i'_{p}}R_{j'_{1}}^{j_{1}}\cdots R_{j'_{q}}^{j_{q}}T_{j_{1},\ldots ,j_{q}}^{i_{1},\ldots ,i_{p}}[\mathbf {f} ].$

The definition of a tensor as a multidimensional array satisfying a transformation law traces back to the work of Ricci.^[4] Nowadays, this definition is still used in some physics and engineering text books.^[5]^[6]

التطبيقات

للموتّرات أهمية كبيرة في الفيزياء والهندسة. ففي مجال تصوير موتّر الحلول diffusion tensor imaging، يعبر الموتّر عن النفاذية التفاضلية للمركبات العضوية إلى الماء ليعطي مسحاً للدماغ.

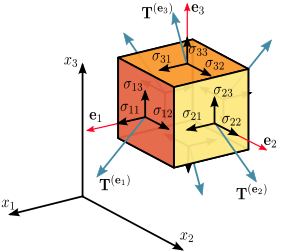
أما أهم تطبيقات الموتّر في الهندسة التطبيقية (المدنية خصوصا) فهو موتّر الإجهاد stress tensor وموتّر التشوه strain tensor، وكلاهما موتّرات من الرتبة الثانية ويرتبطان بمادة خطية عامة عن طريق موتّر المرونة elasticity tensor ذو الرتبة الرابعة.

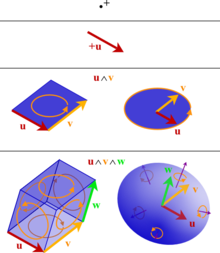
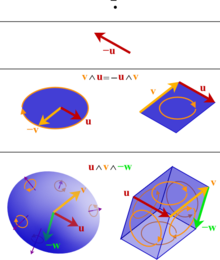
المتجهات مثلا تعتبر موتّرات من الدرجة الأولى والموتّر في حد ذاته هو ذلك الشعاع الذي نرسمه على الورقة مثلا أما الشعاع أو المتجه فما هو إلا مظهر من تمظهرات الموتّر حيث يمكننا أن نكتب الموتّر في قواعد مختلفة تعطينا إحداثيات مختلفة للمتجه.

أمثلة

This table shows important examples of tensors, including both tensors on vector spaces and tensor fields on manifolds. The tensors are classified according to their type (n, m), where n is the number of contravariant indices, m is the number of covariant indices, and n + m gives the total order of the tensor. For example, a bilinear form is the same thing as a (0, 2)-tensor; an inner product is an example of a (0, 2)-tensor, but not all (0, 2)-tensors are inner products. In the (0, M)-entry of the table, M denotes the dimensionality of the underlying vector space or manifold because for each dimension of the space, a separate index is needed to select that dimension to get a maximally covariant antisymmetric tensor.

n, m	n = 0	n = 1	n = 2	n
m = 0	scalar, e.g. scalar curvature	vector (e.g. direction vector)	inverse metric tensor, bivector (e.g., a Poisson structure)	n-vector, a sum of n-blades
m = 1	covector, linear functional, 1-form (e.g. gradient of a scalar field)	linear transformation,^[7] Kronecker delta
m = 2	bilinear form, e.g. inner product, metric tensor, Ricci curvature, 2-form, symplectic form	e.g. cross product in three dimensions	e.g. elasticity tensor
m = 3	e.g. 3-form	e.g. Riemann curvature tensor
...
m = M	e.g. M-form i.e. volume form
...

Raising an index on an (n, m)-tensor produces an (n + 1, m − 1)-tensor; this can be visualized as moving diagonally up and to the right on the table. Symmetrically, lowering an index can be visualized as moving diagonally down and to the left on the table. Contraction of an upper with a lower index of an (n, m)-tensor produces an (n − 1, m − 1)-tensor; this can be visualized as moving diagonally up and to the left on the table.

Orientation defined by an ordered set of vectors.

Reversed orientation corresponds to negating the exterior product.

Geometric interpretation of grade n elements in a real exterior algebra for n = 0 (signed point), 1 (directed line segment, or vector), 2 (oriented plane element), 3 (oriented volume). The exterior product of n vectors can be visualized as any n-dimensional shape (e.g. n-parallelotope, n-ellipsoid); with magnitude (hypervolume), and orientation defined by that on its n − 1-dimensional boundary and on which side the interior is.^[8]^[9]

انظر أيضا

مواضيع ذات علاقة

جبر الموترات

Glossary of tensor theory

Notation

أساسيات

التطبيقات

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

الهامش

المراجع

^ البنك الآلي السعودي للمصطلحات (باسم).
^ معجم المصطلحات على موقع مجمع اللغة العربية بالقاهرة.
^ Sharpe, R. W. (1997). Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. Berlin, New York: Springer-Verlag. p. 194. ISBN 978-0-387-94732-7.
^ خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة Kline
^ Marion, J.B.; Thornton, S.T. (1995). Classical Dynamics of Particles and Systems (4th ed.). Saunders College Publishing. p. 424. ISBN 978-0-03-098967-4.
^ Griffiths, D.J. (1999). Introduction to Electrodynamics (3 ed.). Prentice Hall. pp. 11–12 and 535–. ISBN 978-0-13-805326-0.
^ Paul Bamberg; Shlomo Sternberg (1991). A Course in Mathematics for Students of Physics: Volume 2. Cambridge University Press. p. 669. ISBN 978-0-521-40650-5.
^ R. Penrose (2007). The Road to Reality. Vintage books. ISBN 0-679-77631-1.
^ J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. p. 83. ISBN 0-7167-0344-0.{{cite book}}: CS1 maint: multiple names: authors list (link)

وصلات خارجية

Eric W. Weisstein, موتر at MathWorld.
Introduction to Vectors and Tensors, Vol 1: Linear and Multilinear Algebra by Ray M. Bowen and C. C. Wang.
Introduction to Vectors and Tensors, Vol 2: Vector and Tensor Analysis by Ray M. Bowen and C. C. Wang.
An Introduction to Tensors for Students of Physics and Engineering by Joseph C. Kolecki, Glenn Research Center, Cleveland, Ohio, released by NASA
Foundations of Tensor Analysis for Students of Physics and Engineering With an Introduction to the Theory of Relativity by Joseph C. Kolecki, Glenn Research Center, Cleveland, Ohio, released by NASA
A discussion of the various approaches to teaching tensors, and recommendations of textbooks
Introduction to tensors an original approach by S Poirier
A Quick Introduction to Tensor Analysis by R. A. Sharipov.
Richard P. Feynman's Lecture on tensors.

هذه بذرة مقالة عن الرياضيات تحتاج للنمو والتحسين، ساهم في إثرائها بالمشاركة في تحريرها.

[باسم-1] البنك الآلي السعودي للمصطلحات (باسم).

[مجمع-2] معجم المصطلحات على موقع مجمع اللغة العربية بالقاهرة.

[3] Sharpe, R. W. (1997). Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. Berlin, New York: Springer-Verlag. p. 194. ISBN 978-0-387-94732-7.

[Kline-4] خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة Kline

[5] Marion, J.B.; Thornton, S.T. (1995). Classical Dynamics of Particles and Systems (4th ed.). Saunders College Publishing. p. 424. ISBN 978-0-03-098967-4.

[6] Griffiths, D.J. (1999). Introduction to Electrodynamics (3 ed.). Prentice Hall. pp. 11–12 and 535–. ISBN 978-0-13-805326-0.

[BambergSternberg1991-7] Paul Bamberg; Shlomo Sternberg (1991). A Course in Mathematics for Students of Physics: Volume 2. Cambridge University Press. p. 669. ISBN 978-0-521-40650-5.

[8] R. Penrose (2007). The Road to Reality. Vintage books. ISBN 0-679-77631-1.

[9] J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. p. 83. ISBN 0-7167-0344-0.{{cite book}}: CS1 maint: multiple names: authors list (link)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]