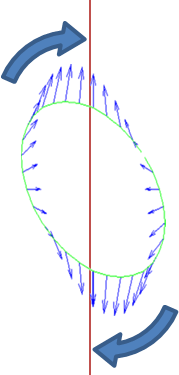
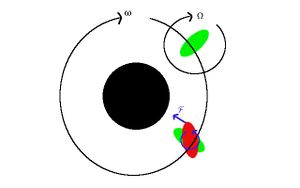
تشوه مدي

Tidal locking results in the Moon rotating about its axis in about the same time it takes to orbit Earth. Except for libration effects, this results in the Moon keeping the same face turned toward Earth, as seen in the left figure. (The Moon is shown in polar view, and is not drawn to scale.) If the Moon were not rotating at all, it would alternately show its near and far sides to Earth, while moving around Earth in orbit, as shown in the right figure.

A side view of the Pluto-Charon system. Pluto and Charon are tidally locked to each other. Charon is massive enough that the barycenter of Pluto's system lies outside of Pluto; thus Pluto and Charon are sometimes considered to be a binary system.

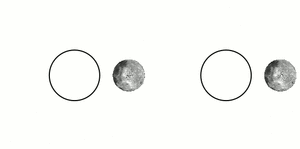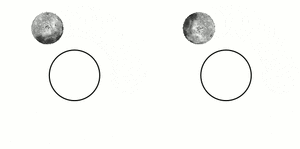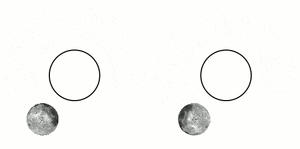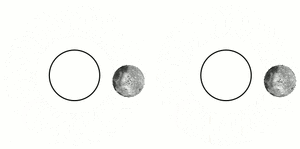
التشوه المدي Tidal distortion أو Tidal locking هو ظاهرة تشوه شكل جرم سماوي بقوة جاذبية جرم آخر فمثلا يمكن أن يتشوه قمر صغير (تشوها ماديا) بقوة جاذبية كوكبه الأم (الاكبر عادة) ويمكن أيضا أن يقترب نجمان أحدهما من الآخر فيشوه أحدهما الآخر تشويها ماديا.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الآلية

If the tidal bulges on a body (green) are misaligned with the major axis (red), the tidal forces (blue) exert a net torque on that body that twists the body toward the direction of realignment

 التغيرات المدارية

If rotational frequency is larger than orbital frequency, a small torque counteracting the rotation arises, eventually locking the frequencies (situation depicted in green)

 Eccentric orbits

A widely spread misapprehension is that a tidally locked body permanently turns one side to its host.

— Heller et al. (2011)

 الحدوث

 الأقمار

Due to tidal locking, the inhabitants of the central body will never be able to see the satellite's green area.

Most major moons in the Solar System − the gravitationally rounded satellites − are tidally locked with their primaries, because they orbit very closely and tidal force increases rapidly (as a cubic function) with decreasing distance. Notable exceptions are the irregular outer satellites of the gas giants, which orbit much farther away than the large well-known moons.

Pluto and Charon are an extreme example of a tidal lock. Charon is a relatively large moon in comparison to its primary and also has a very close orbit. This results in Pluto and Charon being mutually tidally locked. Pluto's other moons are not tidally locked; Styx, Nix, Kerberos, and Hydra all rotate chaotically due to the influence of Charon.

The tidal locking situation for asteroid moons is largely unknown, but closely orbiting binaries are expected to be tidally locked, as well as contact binaries.

 قمر الأرض

Because Earth's Moon is 1:1 tidally locked, only one side is visible from Earth.

Earth's Moon's rotation and orbital periods are tidally locked with each other, so no matter when the Moon is observed from Earth the same hemisphere of the Moon is always seen. The far side of the Moon was not seen until 1959, when photographs of most of the far side were transmitted from the Soviet spacecraft Luna 3.

When the Earth is observed from the moon, the Earth does not appear to translate across the sky but appears to remain in the same place, rotating on its own axis.

 Timescale

An estimate of the time for a body to become tidally locked can be obtained using the following formula:

$t_{\text{lock}}\approx {\frac {\omega a^{6}IQ}{3Gm_{p}^{2}k_{2}R^{5}}}$

where

• $\omega \,$ is the initial spin rate expressed in radians per second,
• $a\,$ is the semi-major axis of the motion of the satellite around the planet (given by the average of the periapsis and apoapsis distances),
• $I\,$ $\approx 0.4\;m_{s}R^{2}$ is the moment of inertia of the satellite, where $m_{s}\,$ is the mass of the satellite and $R\,$ is the mean radius of the satellite,
• $Q\,$ is the dissipation function of the satellite,
• $G\,$ is the gravitational constant,
• $m_{p}\,$ is the mass of the planet, and
• $k_{2}\,$ is the tidal Love number of the satellite.

$Q$ and $k_{2}$ are generally very poorly known except for the Moon, which has $k_{2}/Q=0.0011$. For a really rough estimate it is common to take $Q\approx 100$ (perhaps conservatively, giving overestimated locking times), and

$k_{2}\approx {\frac {1.5}{1+{\frac {19\mu }{2\rho gR}}}},$

where

• $\rho \,$ is the density of the satellite
• $g\approx Gm_{s}/R^{2}$ is the surface gravity of the satellite
• $\mu \,$ is the rigidity of the satellite. This can be roughly taken as 3×10¹⁰ N·m⁻² for rocky objects and 4×10⁹ N·m⁻² for icy ones.

Even knowing the size and density of the satellite leaves many parameters that must be estimated (especially ω, Q, and μ), so that any calculated locking times obtained are expected to be inaccurate, even to factors of ten. Further, during the tidal locking phase the semi-major axis $a$ may have been significantly different from that observed nowadays due to subsequent tidal acceleration, and the locking time is extremely sensitive to this value.

Because the uncertainty is so high, the above formulas can be simplified to give a somewhat less cumbersome one. By assuming that the satellite is spherical, $k_{2}\ll 1\,,Q=100$, and it is sensible to guess one revolution every 12 hours in the initial non-locked state (most asteroids have rotational periods between about 2 hours and about 2 days)

$t_{\text{lock}}\approx 6\ {\frac {a^{6}R\mu }{m_{s}m_{p}^{2}}}\times 10^{10}\ {\text{years}},$

with masses in kilograms, distances in meters, and $\mu$ in newtons per meter squared; $\mu$ can be roughly taken as 3×10¹⁰ N·m⁻² for rocky objects and 4×10⁹ N·m⁻² for icy ones.

There is an extremely strong dependence on semi-major axis $a$.

For the locking of a primary body to its satellite as in the case of Pluto, the satellite and primary body parameters can be swapped.

One conclusion is that, other things being equal (such as $Q$ and $\mu$), a large moon will lock faster than a smaller moon at the same orbital distance from the planet because $m_{s}\,$ grows as the cube of the satellite radius $R$. A possible example of this is in the Saturn system, where Hyperion is not tidally locked, whereas the larger Iapetus, which orbits at a greater distance, is. However, this is not clear cut because Hyperion also experiences strong driving from the nearby Titan, which forces its rotation to be chaotic.

The above formulae for the timescale of locking may be off by orders of magnitude, because they ignore the frequency dependence of $k_{2}/Q$. More importantly, they may be inapplicable to viscous binaries (double stars, or double asteroids that are rubble), because the spin–orbit dynamics of such bodies is defined mainly by their viscosity, not rigidity.

 List of known tidally locked bodies

 Extra-solar

• The most successful detection methods of exoplanets (transits and radial velocities) suffer from a clear observational bias favoring the detection of planets near the star; thus, 85% of the exoplanets detected are inside the tidal locking zone, which makes it difficult to estimate the true incidence of this phenomenon. Tau Boötis is known to be locked to the close-orbiting giant planet Tau Boötis b.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 Bodies likely to be locked

 Solar System

Based on comparison between the likely time needed to lock a body to its primary, and the time it has been in its present orbit (comparable with the age of the Solar System for most planetary moons), a number of moons are thought to be locked. However their rotations are not known or not known enough. These are:

 Probably locked to Saturn

• Daphnis
• Aegaeon
• Methone
• Anthe
• Pallene
• Helene
• Polydeuces

 Probably locked to Uranus

• Cordelia
• Ophelia
• Bianca
• Cressida
• Desdemona
• Juliet
• Portia
• Rosalind
• Cupid
• Belinda
• Perdita
• Puck
• Mab

 Probably locked to Neptune

• Naiad
• Thalassa
• Despina
• Galatea
• Larissa

 خارج المجموعة الشمسية

• Gliese 581c, Gliese 581g, Gliese 581b, and Gliese 581e may be tidally locked to their parent star Gliese 581. Gliese 581d is almost certainly captured either into the 2:1 or the 3:2 spin–orbit resonance with the same star.
• All planets in the TRAPPIST-1 system are likely to be tidally locked.

 انظر أيضا

• المد والجزر
• جاذبية
• Conservation of Angular Momentum
• Gravity-gradient stabilization – a method used to stabilize some artificial satellites
• Orbital resonance
• Planetary habitability
• Roche limit
• Synchronous orbit
• Tidal acceleration

 المصادر

• مؤمن, عبد الأمير (2006). قاموس دار العلم الفلكي. بيروت، لبنان: دار العلم للملايين. {{cite book}}: Cite has empty unknown parameter: |طبعة أولى coauthors= (help)