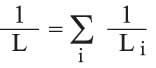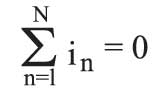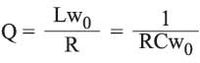دائرة كهربائية
| تحليل خطي للشبكات | |
|---|---|
| العناصر | |
| المكونات | |
| دوائر التوالي والتوازي | |
| تحويلات المعاوقة | |
| مبرهنات المولد | مبرهنات الشبكة |
| أساليب تحليل الشبكات | |
| Two-port parameters | |
الدائرة الكهربائية تنتج دارة كهربائية عن توصيل عدة أجهزة ثنائية الأقطاب مع بعضها بحيث تكون شبكة مغلقة حتى تعمل. ولتبسيط ذلك نأخذ دارة بسيطة تتكون من بطارية ومصباح ومفتاح. عند غلق الدارة تلاحظ إضاءة المصباح وذلك بسب مرور تيار كهربائي.
سميت الدارة الكهربائية بـِدارة لأن تيار كهربائي لا يسري في الدارة إلا إذا كانت الدارة مغلقة مثل الدائرة. وسميت بـِكهربائية لأن عملها يعتمد على الكهرباء. انظر كهرباء.
وتشتمل الدارة الكهربائية عادةً على منبع، كالبطارية أو المولِّد، يقدم الطاقة الكهربائية إلى الشحنات الكهربائية المشكِّلة للتيار، وعلى أدوات تستخدم ذلك التيار كالمصابيح والمحركات الكهربائية وغيرها، وكذلك على أسلاك توصيل أو خطوط نقل.
إن التيار الكهربائي الذي يسري في الموصلات والمحاليل الكهرلية ينشأ نتيجة لحركة أيونات - وهي جزيئات تحمل شحنة كهربائية سالبة أو موجبة - فالالكترونات هي الشحنات المتحركة في المواد الموصلة، والأيونات بنوعيها السالبة أو الموجبة هي الشحنات المتحركة في المحاليل الكهرلية كما تعمل البطارية.
مفتاح التيار يتحكم في إضاءة أو إطفاء المصباح. فهو يعمل على إغلاق الدارة الكهربائية ليمر التيار (حيث تكون الدائرة الكهربائية كاملة) ويضيء المصباح، نقول أن الدارة مغلقة. أو يعمل على فتح الدائرة أو قطعها فلا يمر التيار الكهربائي في الدائرة المقطوعة، ولا يضيء المصباح ونقول أن الدارة مفتوحة.
- ملحوظة: يسمى العمود مصدراً كهربائيا والمصباح مستقبلا. عمود البطارية والمصباح وقاطع التيار (المفتاح) مكونات كهربائية، لكل منها مربطان تسمى ثنائيات القطب. قطب يدخل منه التيار والقطب الآخر يخرج منه التيار.
تتكون الدارة الكهربائية البسيطة من ثنائيات أقطاب موصولة ببعضها بواسطة أسلاك (موصّلة)، وتحتوي على مصدر للتيار ومفتاح ومستقبل (مصباح، أو راديو أو ثلاجة...إلخ).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
الإشارات الكهربائية
تشكل الإشارات ركيزة أساسية في نظرية الدارات، وتُصنف في فئتين أساسيتين: الإشارات المستمرة التي تكون فيها قيمة الإشارة ثابتة مع الزمن، والإشارات المتغيرة مع الزمن. وأكثر إشارات الفئة الثانية استخداماً هي تابع الخطوة والنبضة والإشارات الدورية وعلى الأخص الإشارات المتناوبة.
المقادير الكهربائية
ـ التيار الكهربائي: هو قياس لمعدل مرور الشحنة الكهربائية في الدارة. وتنعكس حركة الشحنات الكهربائية بصورة دورية مع الزمن في التيار المتناوب، في حين تكون الجهة ثابتة في حالة التيار المستمر. وواحدة شدة التيار هي الأمبير (A).
ـ الجهد (فرق الكمون): الجهد بين شفع من الطرفيات هو قياس للعمل المطلوب لتحريك شحنة عبر الدارة التي تصل بينهما. وواحدة الجهد هي الفولط (V).
ـ الاستطاعة: الاستطاعة هي معدل نقل الطاقة الكهربائية، وواحدتها الواط (W). وتُعطى الاستطاعة التي يرمز لها بـ p بالعلاقة:
P = V x i
حيث V هو الجهد وi هو شدة التيار.
ثنائيات الأقطاب
يُسمى ثنائي قطب كل مكوّن ذي قطبين يمرّ فيه تيار i خضع لجهد V والعكس صحيح. وتوجد ثلاث ثنائيات أقطاب مطاوعة أساسية مستخدمة في الدارات الكهربائية هي المقاومة والمكثفة والوشيعة.
ـ المقاومة: هي عنصر يبدد الاستطاعة الكهربائية على شكل حرارة. ويُقال عن مقاومة إنها خطيّة إذا كان مميزها في المستوي (v, i) مستقيماً يمر من المبدأ. ويرمز للمقاومة بالرمز R وواحدتها الأوم. كما يطلق على مقلوب المقاومة اسم الناقلية (σ) وواحدتها سيمنز (S).
يمكن ربط المقاومات على التسلسل (الشكل -1) بحيث يمر فيها التيار ذاته، فيكون ثنائي القطب المكافئ مقاومة قيمتها
أما إذا رُبطت المقاومات على التفرع (الشكل-2) بحيث تخضع كل مقاومة للجهد نفسه فيكون ثنائي القطب المكافئ مقاومة مقلوب قيمتها:
ـ المكثفة: هي عنصر يختزن الطاقة الكهربائية، ويمكنه تحريرها في وقت لاحق. وتتألف المكثفة البسيطة من صفيحتين ناقلتين متوازيتين يفصل بينهما عازل كهربائي، وتكون الشحنة المختزنة في عازل مكثفة مثالية (عديمة الضياع) متناسبة والجهد على طرفيها. ويطلق على ثابت التناسب سعة المكثفة (C) ويقاس بالفاراد (F). ويتناسب تيار شحن المكثفة i(t) ومشتق الجهد v(t) على طرفيها بالنسبة للزمن:
ومن ثَم تشكل المكثفة المثالية دارة مفتوحة ضمن دارة تيار مستمر.
وتُربط المكثفات على التفرع (الشكل-3) فتكون السعة الفعلية للدارة التفرعية:
أما إذا رُبطت على التسلسل (الشكل-4) فيكون مقلوب السعة الفعلية للدارة الكلية:
ـ الوشيعة: هي عنصر يختزن الطاقة المغنطيسية ويمكنه تحريرها في وقت لاحق. إذ ينتج عن مرور تيار في سلك نشوء حقل مغنطيسي حوله، وعندما يُلف السلك على شكل وشيعة فإن الحقل المغنطيسي يزداد قوة. ونسمي التحريضية L للملف وواحدتها الهنري (H) النسبة بين التدفق المغنطيسي بالفيبر (Wb) وتيار التحريض الذي ينشأ عنه بالأمبير. ويتناسب فرق الكمون v(t) على طرفي وشيعة ومشتق التيار i(t) بالنسبة للزمن:
أي أن سلوك الوشيعة يبدو وكأنه قصر دارة ضمن دارة تيار مستمر.
ويمكن ربط الوشائع على التسلسل فتكون التحريضية المكافئة للدارة التسلسلية:
أما إذا رُبطت على التفرع فيكون مقلوب التحريضية المكافئة للدارة التفرعية:
ـ المنبع: المنبع هو عنصر فاعل، أي أنه يقدم الطاقة إلى دارة خارجية مثل المدخرات والمهتزات وغيرها. ويمكن تصنيف المنابع في فئتين: مثالية وعملية. وبإمكان المنبع المثالي نظرياً تقديم كمية لانهائية من الاستطاعة، أما المنبع العملي فيخضع لمحدودية في جهد الخرج والتيار والاستطاعة. كما يُقال عن منبع إنه مستقل إذا كانت كمية الجهد أو التيار التي يقدمها مستقلة عن بقية الدارة، وإلا فهو منبع مرتبط. والمنابع على نوعين منابع التيار ومنابع الجهد.
رباعيات الأقطاب
رباعي الأقطاب هو جزء من شبكة تتصل بالمحيط الخارجي بشفعين من الأطراف فقط، يكوِّن كل منها ثنائي قطب أي أن دور رباعي الأقطاب هو أداة ربط.
ـ التحريض المتبادل: إذا ما جرى لف وشيعتين ضمن الدارة المغنطيسية ذاتها، وتدفق التيار في الوشيعة الأولى مثلاً، فإن جزءاً من التدفق المغنطيسي الناجم عن تلك الوشيعة سيجتاز الوشيعة الثانية، والعكس صحيح. ونسمي التحريضية التبادلية M النسبة بين التدفق المغنطيسي الذي يصل إلى الملف الثاني وتيار التحريض في الملف الأول أو العكس. وواحدة التحريضية التبادلية الهنري أيضاً. ويبين (الشكل -5 ) مثالاً على دارة تيار متناوب تشتمل على مقاومة ومكثفة ووشيعة وتحريضية تبادلية، يمكن النظر إليها كرباعي أقطاب.
ـ المحِّول: هو مجموعة من الوشائع المقترنة اقتراناً قوياً. وهو في الواقع أداة ربط تسمح بتعديل قيم الجهود والتيارات وبمواءمة الممانعات.
تصنيف الدارات
تُصنف الدارات وفقاً لمعايير عدة مرتبطة بطبيعة عناصرها أو بنيتها أو وظيفتها أو تقانتها.
ـ الدارة المطاوعة هي التي لا يمكنها توليد الطاقة أو تضخيمها، أي إذا لم يكن بمقدورها أن تقدم للحمل طاقة تتجاوز تلك التي تُغذى الدارة بها. فإذا لم يكن هناك ضياع في الطاقة يُقال عن الدارة إنها عديمة الضياع. فعلى سبيل المثال إذا تضمنت دارة وشيعة مثالية ومكثفة مثالية فقط من دون مقاومات فهي مطاوعة وعديمة الضياع.
ـ الدارة الخطية التي تتضمن عناصر خطية ومولِّدات مستقلة فقط. ويكون العنصر خطياً إذا بقيت قيمته ثابتة عندما يتغير التيار الذي يجتازه.
ـ الدارة اللامتغيرة مع الزمن التي تحوي عناصر غير متغيرة مع الزمن. ويكون العنصر غير متغير مع الزمن إذا لم يتغير منحني خواصه بمرور الزمن، أي أن العلاقة بين الاستجابة والتحريض تبقى على حالها منم دون لحظة تطبيق التحريض.
ـ توصف الدارة بذات عناصر مجمعة إذا كانت الأبعاد الفيزيائية لكل مكوناتها مهملة مقارنة بطول موجة الإشارة. أما إذا كانت تلك الأبعاد قريبة من طول الموجة فيُقال عن الدارة إنها ذات عناصر موزعة. ويجب في هذه الحالة استخدام علاقات مكسويل لأنها أكثر شمولاً.
ـ يُقال عن دارة إنها صوتية إذا كانت ترددات الإشارات المطبقة صوتية (مثال: مازج إشارات موسيقية)، ويُقال إنها راديوية إذا كانت ترددات الإشارات راديوية (مكبِّرات الاستطاعة في أجهزة الاستقبال الراديوي مثلاً)، ويُقال إنها مكروية إذا كانت ترددات العمل مكروية (مثال: أجهزة الاستقبال الفضائي التلفزيوني).
ـ وأخيراً يُقال عن دارة إنها منفصلة إذا كانت مكونة من عناصر كهربائية منفصلة، كالمقاومات والوشائع والمكثفات، موصولة فيما بينها بأسلاك. ويُقال إنها متكاملة إذا كانت عناصرها مُصنعةً على رقاقة واحدة من أنصاف النواقل.
مبادئ الدارات الكهربائية
ـ قانون أوم: ينص قانون أوم على أن فرق الكمون بين طرفي سلك ناقل يتناسب وشدة التيار، ويٌطلق على ثابت التناسب اسم المقاومة الكهربائية للناقل (R) وواحدتها الأوم(Ω).
V = R x i
ـ قانون جول: ينص هذا القانون على أن كمية الحرارة المنتشرة في وحدة الزمن في ناقل ما، تتناسب مع مقاومته ومع مربع شدة التيار المار فيه.
ـ قانونا كيرشوف: يعتمد قانون كيرشوف للتيار على أن معدل تدفق الشحنات إلى أي نقطة أو عقدة من دارة يساوي معدل تدفق الشحنات الخارجة منها. أي أن المجموع الجبري للتيارات الواردة إلى أي عقدة يساوي المجموع الجبري للتيارات الصادرة منها.
في حين يعتمد قانون كيرشوف للجهد على أنه لن يكون هناك تغير في الكمون الكهربائي لدى القيام بدورة كاملة حول دارة. أي أن المجموع الجبري للقوى المحركة الكهربائية وفروق الكمون حول أي دارة مغلقة معدوم.
الدارات الكهربائية الخطية الأساسية
ـ الدارات الخطية من الدرجة الأولى RC وRL: وهي دارات مكوَّنة من عنصرين أساسيين (مقاومة ومكثفة أو مقاومة ووشيعة) مربوطين على التسلسل أو على التفرع. وتُوصف هذه الدارات بأنها من الدرجة الأولى لأن المعادلة التفاضلية التي تحكم الدارة هي من الدرجة الأولى. وسنكتفي بإيضاح الدارات RC نظراً للازدواجية بينها وبين الدارات RL.
ـ الدارات RC التسلسلية: إذا طُبق على دارة RC تسلسلية منبع جهد من نوع خطوة فإن التيار البدائي يتناقص وفق الثابت الزمني RC في حين يزداد الجهد على طرفي المكثفة ليبلغ 99% من القيمة النهائية (الحالة الدائمة) خلال زمن t=5tτ فقط. وتمثل هذه الدارة عملية شحن المكثفة. فإذا حُذف منبع الجهد واستعيض عنه بقصر دارة حصلت عملية التفريغ.
وبتطبيق إشارة جيبية على الدارة، المؤلفة من مقاومة R ومكثفة سعتها C، وأخذ جهد الخرج على طرفي المكثفة، نحصل على دارة مرشح تمرير عال، يعطى تردد قطعها بالعلاقة:
وتُستخدم هذه الدارات أيضاً كدارات إزاحة للطور.
ـ الدارات RC التفرعية: إذا كانت لدينا دارة RL تفرعية مطبق عليها تيار من نوع خطوة، فإن الدراسة والنتائج متماثلة مع إبدال الجهد بالتيار.
ـ الدارات الخطية من الدرجة الثانية RLC: وهي الدارات الدينامية التي تتضمن مكثفتين أو وشيعتين أو مكثفة وحيدة ووشيعة واحدة. ويوجد نوعان من الدارات RLC التسلسلية والتفرعية، وسنكتفي بعرض الدارة التسلسلية نظراً للتقابل بينها وبين الدارة التفرعية.
ـ الدارة RLC التسلسلية: لهذه الدارة (الشكل-6) في النمط الجيبي أهمية خاصة تتجلى في كونها أبسط دارة يمكن بوساطتها دراسة ظواهر التجاوب.
ويُسمى نبض التجاوب w0 للدارة النبض الذي يكون التيار من أجله أعظمياً، ويعطى بالعلاقة:
حيث L تحريضية الوشيعة وC سعة المكثفة.
ونحصل بين طرفي الوشيعة (أو المكثفة) عند تردد التجاوب على جهد أعلى بـ Q مرة من جهد المنبع. ويُطلق على هذه الظاهرة اسم فرط الجهد. ويميز عامل فرط التوتر (الفولطية) Q حدَّة التجاوب ويعطى بالعلاقة:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
أهمية تدريس الدارات الكهربائية
يحتاج المهندس الكهربائي في عمله إلى تصميم الدارات وتحليلها. وقد أدت التطورات التقانية والتقنية خلال العقدين الأخيرين إلى تغييرات جذرية في طرائق التصميم والعمل الهندسي، ووفرت أدوات جديدة كالتصميم بمساعدة الحاسوب، والتصنيع بمساعدة الحاسوب.
ومع ذلك، فإنه من الضروري ترسيخ المبادئ والنظريات الأساسية والتمكن من طرائق التحليل والحساب ومن الأدوات الرياضية كتحويل لابلاس، بُغية فهم أعمق لطبيعة العمليات التي يجريها الحاسوب، واختيار أدق للنموذج الملائم للعنصر، واستثمار أفضل للنتائج.
تطبيقات الدارات الكهربائية
للدارات الكهربائية تطبيقات في معظم الأنظمة التي تحيط بنا، كالحواسيب الشخصية والتلفاز وشبكات الطاقة الكهربائية وأنظمة الاتصالات والتحكم وغيرها. وتوجد تطبيقات أساسية للدارات الكهربائية نذكر منها على سبيل المثال لا الحصر المرشحات.
ـ المرشحات: المرشح الكهربائي هو جهاز أو نظام مصمم لفصل وتمرير إشارة معينة مرغوبة من خليط من الإشارات المرغوبة وغير المرغوبة.
إن أبسط المرشحات هي مقاطع التمرير المنخفض والعالي RC من الدرجة الأولى والتي لها دوماً ربح في حزمة التمرير أقل بقليل من الواحد. ويمكن تنفيذ مرشحات من درجات أعلى بوضع عدة مقاطع RC قاعدية على التعاقب. وكلما ازدادت درجة المرشح اقتربت استجابته من استجابة المرشح المثالي..[1].
ويمكن بناء المرشحات باستخدام العناصر LC فقط كما هو مبين في الشكل (7).
طرق تحليل الدوائر الكهربائية
طرق التحليل هي طرق يمكن من خلالها معرفة قيم ومتغيرات جميع عناصر الدوائر الكهربائية من خلال معرفة بعضها. مثال على ذلك : إذا أردت الحصول على تيار كهربائي يساوي 1 مل أمبير وأنا أمتلك مصباحا كهربائيا ً مقاومته 200 أوم. فإنني أقوم بحساب فرق الجهد من خلال قانون أوم:
- ج = م * ت
- ج = 200*0.001
- ج = 0.2 فولت
إذن فإنني بحاجة إلى بطارية بفرق جهد مقداره0.2 من الفولت.
1) ومن أهم وأبسط قوانين التيار الكهربائي هو :قانون أوم الذي يتحدث عن علاقة التيار الكهربائي ويرمز له (ت) أو (i) وفرق الجهد ويرمز له (ج) أو (V) وقيمة مقاومة التيار ويرمز لها (م) أو (R). والمعادلة التالية هي الصيغة المبسّطة لقانون أوم.
(ج = م * ت أو V = I*R )
2) قانونا كيرشوف وهما قانونان يستخدمان في حل الدوائر الكهربائية:
- قانون التيار: وينص على أن مجموع التيارات الداخلة إلى نقطة تفرع يساوي مجموع التيارات الخارجة. وهو ناشئ من مبدأ حفظ الشحنة الكهربائية أنظر قانون بقاء الشحنة.
- قانون الجهد: وينص على أن مجموع فروق الجهود على حلقة مغلقة يساوي صفراً. أي أنه لا يتغير جهد كهربائي عند نقطة إذا خرجنا منها ثم عدنا إليها عبر مسار مغلق. وهو ناشئ من مبدأ حفظ الطاقة أنظر بقاء الطاقة.
- نظرية ثيفنين تنص على أن أي طرفين في الدارة (قابس كهربائي على سبل المثال) يمكن استبدالهما بـمصدر جهد واحد موصول على التوالي مع مقاومة واحدة.
- ونظرية نورتون تنص على أن أي طرفين في الدارة يمكن استبدالهما بـمصدر تيار وحيد موصول على التوازي مع مقاومة واحدة.
- ويمكن الإثبات رياضيا ً أن قيمة المقاومة الناتجة عن نظرية ثيفنين والناتجة عن نظرية نورتون لنفس الطرفين في نفس الدارة. تكون قيمتها متساوية. وأنه يمكن التحويل بين قيمة مصدر الجهد في دارة ثيفنين وقيمة مصدر التيار في دارة نورتون باستخدام قانون أوم وتعويض قيمة المقاومة المكافئة.
م(ثيفنين) = م (نورتون)
4) نظرية التراكب: إنگليزية: Superposition وهذه النظرية عامة تستخدم في أي نظام خطي. وتنص على أنه لكل نظام يحتوي على أكثر من مصدر (بالإنجليزية Source) يشتركون في التأثير على الناتج أو المخرج (بالإنجليزية Output أو Sink). فإنه يمكن حساب المخرج أو الناتج الكلي من خلال حساب المجموع الجبري لكل نواتج كل مصدر على حدة عند تخميد(عدم تفعيل) بقية المصادر في كل مرة. لنأتي إلى الدوائر الكهربائية: يتم حساب الناتج وهو التيار الكهربائي أو الجهد الكهربائي في نقطة معينة في الدارة الكهربائية كالتالي:
- نختار مصدر تيار أو مصدر جهد ونقوم بإلغاء تفعيل بقية مصارد التيار والجهد على النحو الآتي:
- مصدر جهد يصبح دارة مغلقة أو ما يسمى بالدارة القصيرة.
- مصدر التيار يصبح دارة مفتوحة.
- المصادر المعتمدة على مصادر أخرى لا تتغير.
- نقوم بحساب الناتج المعين حسب الحاجة على فرض أن المصدر الفعال الوحيد هو المصدر الذي اخترناه.
- نعيد حساب الناتج باختيار مصدر آخر وتخميد المصادر الباقية. بمعنىاعادة الخطوة 1 و 2 .
- الناتج النهائي يساوي المجموع الجبري للنواتج الجزئية التي حسبناها في الخطوات السابقة.
الناتج النهائي = ناتج1 + ناتج2 + ناتج 3+.... + ناتج ن
تمثيل الدارة الكهربائية
لتمثيل الدارة الكهربائية نستعمل رموزا لمختلف عناصرها:
- سلك
- مبدال أو مفتاح كهربائي
- مصباح كهربائي
- مصدر : بطارية أو مولد كهربائي
- ثنائي أقطاب
- مقاومة
- مكثف
- ملف
- "الذاكرة المقاومة" ممرستور
أنواع التوصيل
قي الدائرة الكهربائية وباختلاف نوع التيار الذي يسير في الدائرة سواء إذا كان تيار متردد أو تيار مستمر أو باختلاف مكونات الدائرة فان أنواع التوصيل:
- توصيل توالى.
- توصيل توازي.
- لمزيد من المعلومات عند دوائر التوالي والتوازي اقرأ أيضاً دارة التوالي أو التوازي.
- توصيل باي أو توصيل النجمة.
- لحل مثل هذه الدوائر راجع Y-Δ transform للغة الإنجليزية, أو Théorème de Kennelly للغة الفرنسية.
اقرأ أيضاً
- Analysis of resistive circuits
- Alternating current
- Bridge circuit
- Digital circuit
- Circuit diagram
- Circuit theory
- Diode bridge
- Direct current
- Quiescent current
- Ground (electricity)
- Hydraulic analogy
- Impedance
- Load
- Mathematical methods in electronics
- Memristor
- Netlist
- Network analyzer (electrical)
- Network analysis (electrical circuits)
- RC circuit
- LC circuit
- RLC circuit
- Lumped and distributed element model
- Potential divider
- Prototype filter
- Schematic
- Series and parallel circuits
- Superposition theorem
- SPICE
- Topology (electronics)
- Continuity test
- Voltage drop
- Mesh analysis
- كهرباء
- معاوقة
- هندسة كهربائية
- دائرة مقاومة ومكثف
- دائرة مقاومة وملف
- مرشح تردد عالي
- مرشح الكتروني
- قانون أوم
- دارة التوالي أو التوازي
- نظرية ثيفينين
- ترانزستور
- الالات الكهربائية الهندسية
- مكون إلكتروني
- ثنائي أقطاب غير فعال
- ^ "الدارات الكهربائية". الموسوعة العربية. 2007.