نجمة عشارية
| Regular decagram | |
|---|---|
 A regular decagram | |
| النوع | مضلع منتظم |
| الأضلاع والرؤوس | 10 |
| رمز شلفلي | {10/3} t{5/3} |
| مخططات كوكستر-دنكن | {{{p10/3-CD2}}} |
| مجموعة التماثل | Dihedral (D10) |
| الزاوية الداخلية (الدرجات) | 72° |
| الخصائص | نجم، cyclic, equilateral, isogonal, isotoxal |
| المضلعات النجمية |
|---|
|
|
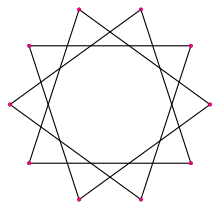
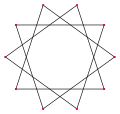
في الهندسة، النجمة العشارية decagram، هي مضلع نجمي بعشر رؤوس. وهناك نجمة عشرية منتظمة واحدة، تضم رؤوس مشلع عشري منتظم، ولكن متصلة بكل ثالث رأس. رمز شلفلي لها هو {10/3}.[1]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
نجمة عشارية منتظمة
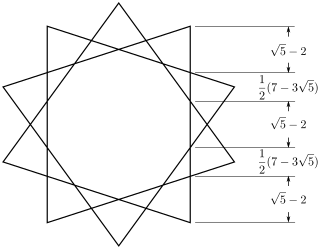
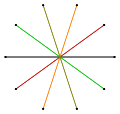
For a regular decagram with unit edge lengths, the proportions of the crossing points on each edge are as shown below.
التطبيقات
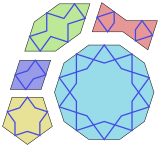
Decagrams have been used as one of the decorative motifs in girih tiles.[2]
أشكال ذات صلة
A regular decagram is a 10-sided polygram, represented by symbol {10/n}, containing the same vertices as regular decagon. Only one of these polygrams, {10/3} (connecting every third point), forms a regular star polygon, but there are also three ten-vertex polygrams which can be interpreted as regular compounds:
- {10/5} is a compound of five degenerate digons 5{2}
- {10/4} is a compound of two pentagrams 2{5/2}
- {10/2} is a compound of two pentagons 2{5}.[3][4]
| الشكل | Convex | المركب | المضلع النجمي | المركـّبات | |
|---|---|---|---|---|---|
| Image | 
|

|
|

|
|
| Symbol | {10/1} = {10} | {10/2} = 2{5} | {10/3} | {10/4} = 2{5/2} | {10/5} = 5{2} |
| Quasiregular | Isogonal | Quasiregular Double covering | |
|---|---|---|---|
 t{5} = {10} |

|

|
 t{5/4} = {10/4} = 2{5/2} |
 t{5/3} = {10/3} |

|

|
 t{5/2} = {10/2} = 2{5} |
رموز
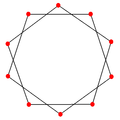 {10/2} or 2{5} is a compound of 2 pentagons. |
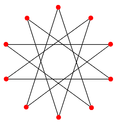 {10/4} or 2{5/2} is a compound of 2 pentagrams. |
نجوم عشارية أخرى
انظر أيضا
الهامش
- ^ Barnes, John (2012), Gems of Geometry, Springer, pp. 28–29, ISBN 9783642309649, https://books.google.com/books?id=7YCUBUd-4BQC&pg=PA28.
- ^ Sarhangi, Reza (2012), "Polyhedral Modularity in a Special Class of Decagram Based Interlocking Star Polygons", Bridges 2012: Mathematics, Music, Art, Architecture, Culture, pp. 165–174, http://archive.bridgesmathart.org/2012/bridges2012-165.pdf.
- ^ Regular polytopes, p 93-95, regular star polygons, regular star compounds
- ^ Coxeter, Introduction to Geometry, second edition, 2.8 Star polygons p.36-38