متعدد الأضلع (هندسة)
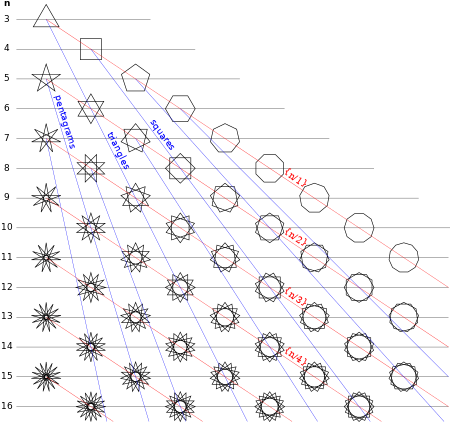
In geometry, a generalized polygon can be called a polygram, and named specifically by its number of sides. All polygons are polygrams, but can also include disconnected sets of edges, called a compound polygon. For example, a regular pentagram, {5/2}, has 5 sides, and the regular hexagram, {6/2} or 2{3}, has 6 sides divided into two triangles.
A regular polygram {p/q} can either be in a set of regular star polygons (for gcd(p,q) = 1, q > 1) or in a set of regular polygon compounds (if gcd(p,q) > 1).[1]
أصل الاسم
The polygram names combine a numeral prefix, such as penta-, with the Greek suffix -gram (in this case generating the word pentagram). The prefix is normally a Greek cardinal, but synonyms using other prefixes exist. The -gram suffix derives from γραμμῆς (grammos) meaning a line.[2]
المضلعات المنتظمة المعممة
A regular polygram, as a general regular polygon, is denoted by its Schläfli symbol {p/q}, where p and q are relatively prime (they share no factors) and q ≥ 2. For integers p and q, it can be considered as being constructed by connecting every qth point out of p points regularly spaced in a circular placement.[3][1]
 {5/2} |
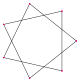 {7/2} |
 {7/3} |
 {8/3} |
 {9/2} |
 {9/4} |
 {10/3}... |
المضلعات المركبة المنتظمة
In other cases where n and m have a common factor, a polygram is interpreted as a lower polygon, {n/k, m/k}, with k = gcd(n,m), and rotated copies are combined as a compound polygon. These figures are called regular compound polygons.
| Triangles... | Squares... | Pentagons... | Pentagrams... | ||||
|---|---|---|---|---|---|---|---|
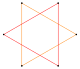 {6/2}=2{3} |
 {9/3}=3{3} |
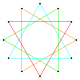 {12/4}=4{3} |
 {8/2}=2{4} |
 {12/3}=3{4} |
 {10/2}=2{5} |
 {10/4}=2{5/2} |
 {15/6}=3{5/2} |
انظر أيضاً
المراجع
- ^ أ ب Eric W. Weisstein, Polygram at MathWorld.
- ^ γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ Coxeter, Harold Scott Macdonald (1973). Regular polytopes. Courier Dover Publications. p. 93. ISBN 978-0-486-61480-9.
- Cromwell, P.; Polyhedra, CUP, Hbk. 1997, ISBN 0-521-66432-2. Pbk. (1999), ISBN 0-521-66405-5. p. 175
- Grünbaum, B. and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)
- Robert Lachlan, An Elementary Treatise on Modern Pure Geometry. London: Macmillan, 1893, p. 83 polygrams. [1]
- Branko Grünbaum, Metamorphoses of polygons, published in The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994)