دوال مثلثية
| حساب المثلثات |
|---|
 |
| المراجع |
| القوانين والمبرهنات |
| الحسبان |
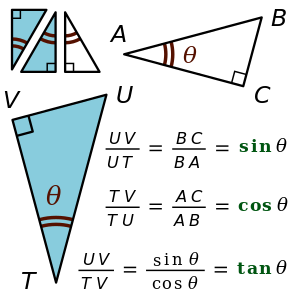
في الرياضيات، تعتبر التوابع المثلثية أو الدوال المثلثية دوال لزاوية هندسية، وهي دوال مهمة عندما نريد دراسة مثلث أو عرض ظواهرِ دورية. يمكن تعريف هذه الدوال كنسبة لأضلاع مثلث قائم الذي يَحتوي تلك الزاويةَ أَو بشكل أكثر عمومية كإحداثيات على دائرة مثلثية أو دائرة واحدية unit circle .
في الرياضيات ، الدوال المثلثية هي دوال ترتبط بالزاوية، وهي مهمة في دراسة المثلثات وتمثيل الظواهر المتكررة (كالموجات). ويمكن تعريف الدوال المثلثية على أنهم نسب بين ضلعين في مثلث قائم فيه الزاوية المعنية، أو ، وبشكل أوسع. كنسبة بين إحداثيات نقاط على دائرة الوحدة، ويعتبر دوما عند الإشارة إلى المثلثات ان الحديث يدور حول مثلث في سطح مستوي (مستوى إحداثي أو إقليدي) ، وذلك ليكون مجموع الزوايا 180 درجة دائما.
وهناك ثلاثة دوال مثلثية أساسية هي:
- جا أو الجيب ، ويساوي النسبة بين الضلع المقابل للزاوية مقسوما على الوتر.
- جتا أو جيب التمام ، ويساوي النسبة بين الضلع المجاور للزاوية مقسوما على الوتر.
- ظا أو الظل ، ويساوي النسبية بين الضلع المقابل للزاوية والضلع المجاور لها.
| اسم التابع | الاختصار | العلاقة |
| جيب | sin أو حب أو جا | |
| تجيب أو جيب تمام | cos ، تجب أو جتا | |
| ظل | tan ، طل أو ظا | |
| تظل أو ظل تمام | cot ، تظل أو ظتا | |
| Secantأو قاطع | sec أو قا | |
| Cosecant أو قاطع تمام | csc أو قتا |
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
علاقات مثلثية
تمثيل بياني لدالة جيب التمام
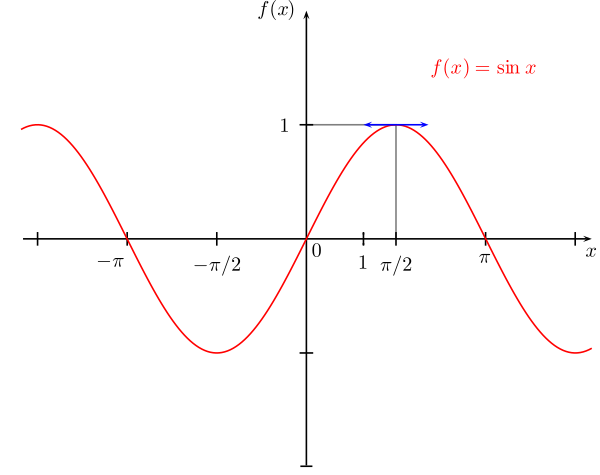
تمثيل بياني لدالة الجيب
القيم الجبرية

The algebraic expressions for the most important angles are as follows:
Writing the numerators as square roots of consecutive non-negative integers, with a denominator of 2, provides an easy way to remember the values.[1]
Such simple expressions generally do not exist for other angles which are rational multiples of a straight angle. For an angle which, measured in degrees, is a multiple of three, the sine and the cosine may be expressed in terms of square roots, see Trigonometric constants expressed in real radicals. These values of the sine and the cosine may thus be constructed by ruler and compass.
For an angle of an integer number of degrees, the sine and the cosine may be expressed in terms of square roots and the cube root of a non-real complex number. Galois theory allows proving that, if the angle is not a multiple of 3°, non-real cube roots are unavoidable.
For an angle which, measured in degrees, is a rational number, the sine and the cosine are algebraic numbers, which may be expressed in terms of nth roots. This results from the fact that the Galois groups of the cyclotomic polynomials are cyclic.
For an angle which, measured in degrees, is not a rational number, then either the angle or both the sine and the cosine are transcendental numbers. This is a corollary of Baker's theorem, proved in 1966.
Simple algebraic values
The following table summarizes the simplest algebraic values of trigonometric functions.[2] The symbol ∞ represents the point at infinity on the projectively extended real line; it is not signed, because, when it appears in the table, the corresponding trigonometric function tends to +∞ on one side, and to –∞ on the other side, when the argument tends to the value in the table.
In calculus
Definition by differential equations
Sine and cosine are the unique differentiable functions such that
Differentiating these equations, one gets that both sine and cosine are solutions of the differential equation
Applying the quotient rule to the definition of the tangent as the quotient of the sine by the cosine, one gets that the tangent function verifies
Power series expansion
Applying the differential equations to power series with indeterminate coefficients, one may deduce recurrence relations for the coefficients of the Taylor series of the sine and cosine functions. These recurrence relations are easy to solve, and give the series expansions[3]
More precisely, defining
- Un, the nth up/down number,
- Bn, the nth Bernoulli number, and
- En, is the nth Euler number,
one has the following series expansions:[4]
See also
- All Students Take Calculus – a mnemonic for recalling the signs of trigonometric functions in a particular quadrant of a Cartesian plane
- Bhaskara I's sine approximation formula
- Differentiation of trigonometric functions
- Generalized trigonometry
- Generating trigonometric tables
- Hyperbolic function
- List of integrals of trigonometric functions
- List of periodic functions
- List of trigonometric identities
- Polar sine – a generalization to vertex angles
- Proofs of trigonometric identities
- Versine – for several less used trigonometric functions
Notes
- ^ Larson, Ron (2013). Trigonometry (9th ed.). Cengage Learning. p. 153. ISBN 978-1-285-60718-4. Archived from the original on 2018-02-15. Extract of page 153 Archived 2018-02-15 at the Wayback Machine
- ^ Abramowitz, Milton and Irene A. Stegun, p. 74
- ^ See Ahlfors, pp. 43–44.
- ^ Abramowitz; Weisstein.
خطأ استشهاد: الوسم <ref> ذو الاسم "Klein_1924" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Klein_2004" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Heng" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Aigner_2000" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Remmert_1991" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Kannappan_2009" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Allen_1976" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Farlow_1993" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Folland_1992" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Boyer_1991" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Gingerich_1986" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "mact-biog" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Fincke" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Bourbaki_1994" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Gunter_1620" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "Roegel_2010" المُعرّف في <references> غير مستخدم في النص السابق.
<ref> ذو الاسم "Plofker_2009" المُعرّف في <references> غير مستخدم في النص السابق.References
- قالب:AS ref
- Lars Ahlfors, Complex Analysis: an introduction to the theory of analytic functions of one complex variable, second edition, McGraw-Hill Book Company, New York, 1966.
- Boyer, Carl B., A History of Mathematics, John Wiley & Sons, Inc., 2nd edition. (1991). ISBN 0-471-54397-7.
- Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software (1991).
- Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics, 2nd ed. Penguin Books, London. (2000). ISBN 0-691-00659-8.
- Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
- Maor, Eli, Trigonometric Delights, Princeton Univ. Press. (1998). Reprint edition (2002): ISBN 0-691-09541-8.
- Needham, Tristan, "Preface"" to Visual Complex Analysis. Oxford University Press, (1999). ISBN 0-19-853446-9.
- Nielsen, Kaj L. (1966), Logarithmic and Trigonometric Tables to Five Places (2nd ed.), New York: Barnes & Noble
- O'Connor, J. J., and E. F. Robertson, "Trigonometric functions", MacTutor History of Mathematics archive. (1996).
- O'Connor, J. J., and E. F. Robertson, "Madhava of Sangamagramma", MacTutor History of Mathematics archive. (2000).
- Pearce, Ian G., "Madhava of Sangamagramma", MacTutor History of Mathematics archive. (2002).
- Protter, Murray H.; Morrey, Charles B., Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley
- Weisstein, Eric W., "Tangent" from MathWorld, accessed 21 January 2006.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
External links
- Hazewinkel, Michiel, ed. (2001), "Trigonometric functions", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Visionlearning Module on Wave Mathematics
- GonioLab Visualization of the unit circle, trigonometric and hyperbolic functions
- q-Sine Article about the q-analog of sin at MathWorld
- q-Cosine Article about the q-analog of cos at MathWorld
















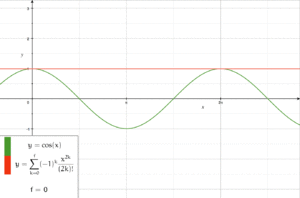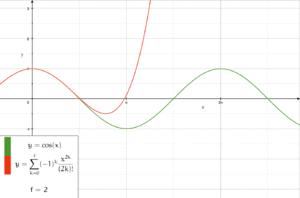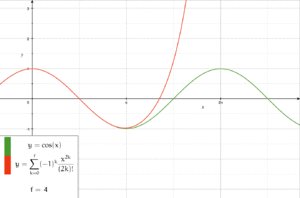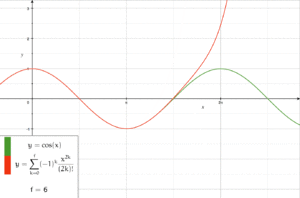
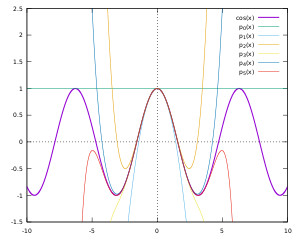





![{\displaystyle {\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}\\[8pt]\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.\end{aligned}}}](https://www.marefa.org/api/rest_v1/media/math/render/svg/8b96cbd9a749c461b481fbd08d70ed37ebb8efd1)




