إسقاط الخرائط
إسقاط الخرائط هو أي طريقة تستخدم في علم رسم الخرائط (كارتوغرافيا)من أجل إظهار السطح المنحني ثنائي البعد للأرض بشكل مستوي. إن كلمة إسقاط تعني أي عمل موجود على سطح الأرض وله قيم على المستوي وليس بالضرورة أن يكون إسقاط هندسي. الخرائط المسطحة لا يمكن أن تظهر بدون عملية الإسقاط، إن الخرائط المسطحة قد تكون أكثر فائدة من الكروية *الإسقاط على الكرة الأرضية في كثير من الحالات
- تكون أصغر وإمكانية تخزينها أسهل:
- يمكنها أن تتوافق مع مساحة كبيرة من المقاييس
- إمكانية إظهارها على شاشة الكمبيوتر أسهل
من أجل تسهيل الدراسة عادة يتم افتراض أن السهل الذي يتم اسقاطه هو عبارة عن سطح كروي، بينما في الواقع يكون الشكل الأنسب لتمثيل الكرة الأرضية هو سطح كروي مفلطح، وهناك العديد من الأجسام السماوية ذات الأشكال الغير منتظمة. ولذلك وبشكل عام فإن إسقاط الخرائط يطلق على طريقة الإسقاط المستوي لسطوح الأجسام الفلكية إلى مستوي.
كلمة الإسقاط المستخدمة هنا لا تنحصر فقط في الإسقاط المنظوري كالذي ينتج عند إسقاط خيال على شاشة، بل إن معنى الإسقاط هو أي تابع رياضي ينقل أي سطح منحني إلى المستوي.
برهن كارل فريدريش غاوس في مبرهنة إغريغوم أنه لا يمكن تمثل الكرة على المستوي بدون تشويه. وبما أن أي طريقة لتمثيل سطح كروي على مستوي هو إسقاط خريطة، عليه يكون أي إسقاط خريطة مشوه. إن كل إسقاط للخرائط يتشوه بشكل مختلف، وتكون دراسة إسقاط الخرائط هي دراسة خصائص التشويه الذي تتعرض له.
الخريطة هي تمثيل للسطح المنحني على المستوي. وعليه فإن تم استخدام إسقاط الخرائط من أجل الحصول على الخرائط، ولا يمكن رسم الخرائط بدون عمل إسقاط خرائط. تتميز الخرائط المستوية عن الخرائط الكروية بأنها أسهل للتعامل وتأخذ حجم تخزيني أصغر، ومن الممكن مشاهدتها بسهولة على شاشة الحاسوب، ومن الممكن أخذ القياسات بسهولة ومن الممكن الاطلاع على أجزاء أكبر من الأرض في وقت واحد، وتكون أرخص من حيث كلفة الانتاج وأسهل للحمل.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
الخصائص المترية للخرائط

هناك الكثير من الخصائص الممكن قياسها على سطح الكرة الأرضية بغض النظر عن الطبيعة الجغرافية للمنطقة. من هذه الخصائص:
يتم إسقاط الخرائط للحفاظ على واحدة أو أكثر من هذه الخصائص، ولكن لا يمكن المحافظة على جميعهم في إسقاط واحد. حيث أن الهدف من استخدام الخريطة يحدد أي إسقاط يجب استخدامه، حيث يوجد العديد من الإسقاطات باختلاف أهداف استخدام الخرائط. من العوامل الأخرى الواجب مراعاتها عند اختيار نوع الاسقاط هو توافق البيانات الجغرافية. إن الأنماط المختلفة تعطي إحداثيات متباينة قليلاً للموقع ذاته من الأرض، لذلك من الضروري توافق البيانات للمواقع الجغرافية.
إنشاء مسقط خريطة
يتضمن إنشاء مسقط خريطة ثلاث خطوات:
- اختيار نموذج لشكل الأرض أو الكوكب المعين (عادة إما كرة أو كرة مفلطحة). وبسبب أن شكل الأرض هو غير منتظم، يتم فقد بعض المعلومات في هذه المرحلة.
- نقل الإحداثيات الجغرافية (خط الطول وخط العرض) إلى الاحداثيات المستوية (سينات وعينات x,y).
- تصغير المقياس (لا يهم ترتيب إجراء الخطوتين الثانية والثالثة).
إن أي إسقاط للخرائط هو ليس "إسقاطاً" فعلياً بالمعنى الفيزيائي للإسقاط، بل هو عبارة عن تطبيق صيغ رياضية ليس لها مقابل فيزيائي. لكن من أجل فهم طبيعة إسقاط الخرائط بشكل أفضل من الممكن تخيل منبع ضوئي موضوع عند نقطة معينة بالنسبة للأرض، وتسقط الخريطة الكروية على مستوي.
اختيار سطح الاسقاط

يطلق على السطح القابل للإسقاط إلى سطح مستوي بدون أي تمدد، أو تمزق أو تقلص اسم "سطح قابل للنشر" إنگليزية: developable surface. إن الاسطوانة، المخروط وبالطبع المستوي تعتبر جميعها سطوح قابلة للنشر. وكما تم عرضه في المقدمة فإن أي اسقاط لسطح كروي على سطح مستوي سوف يؤدي إلى تشوه في الصورة (مثلاً لا يمكنك تسطيح قشرة برتقالة دون تمزيقها أو لفها). أحد الطرق للحصول على المسقط هو إسقاط سطح الأرض إلى أحد السطوح القابلة للنشر مثل السطح الاسطواني أو المخروطي، ومن ثم فتح هذا السطح للحصول على مستوي. على الرغم من أن الخطوة الأولى سوف تنتج بعض التشوه في الصورة، إلا أنه في الخطوة الثانية سيتم تمديد السطح دون أي تشويه إضافي.
توجيه المسقط
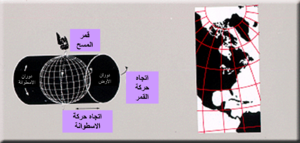
عندما يتم اختيار نوع الإسقاط بين الاسطواني أو المخروطي أو المستوي، يجب تحديد توجيه الشكل. التوجيه يعبر عن وضعية الشكل بالنسبة للكرة. من الممكن أن يكون توجيه سطح الاسقاط ناظمياً أو مستعرضاً أو مائلاً. والسطوح قد تكون مماسية أي أنها تمس الكرة لكن لا تقطعها، أو قاطعة حيث يكون السطح قاطعاً للكرة.
تحجيم
الكرة الجغرافية هي الوسيلة الوحيدة لتمثيل الكرة الأرضية عند تحجيم ثابت في جميع نقاط الخريطة وفي جميع الاتجاهات. أما الخريطة فلا يمكنها تحقيق هذه الخاصية مهما كانت المساحة صغيرة. ولكن من الممكن أن تحقق تحجيماً ثابتاً عند خطوط معينة. بعض الخصائص الممكنة هي:
- يعتمد التحجيم على الموقع، وليس على الاتجاه.
- يكون التحجيم ثابتاً عند أي خط موازي في اتجاه التوازي.
- يعتمد التحجيم على خطوط العرض فقط، وليس على خطوط الطول أو الاتجاه
اختيار نموذج لتمثيل شكل الأرض
يتأثر إنشاء المسقط بكيفية تقريب شكل الأرض. في هذه المقالة يفترض أن الشكل كروي. لكن في واقع الحال فإن شكل الأرض ليس كروياً مثالياً وإنما أقرب إلى شكل القطع الناقص وهو الشكل الذي يتفلطح عند خط الاستواء. عند اختيار تموذج شكل الأرض يجب مراعاة ميزات وسيئات هذا النموذج بالمقارنة مع الشكل البيضوي للأرض. إن النماذج الكروية مناسبة لتمثيل الخرائط الصغيرة مثل أطلس العالم أو الكرة الجغرافية وذلك لأن الخطأ عند ذلك المقياس لا يكون ذا قيمة كبيرة أو كافياً لتبرير استخدام نماذج أعقد في التمثيل. النماذج القطع ناقصية تستخدم في تمثيل الخرائط الطبوغرافية ومن أجل خرائط ذات أحجام متوسطة أو كبيرة التي تكون بحاجة لدقة أعلى لتصوير سطح الأرض.
هناك نموذج آخر لتمثيل سطح الأرض يدعى نموذج جيود geoid والذي هو عبارة عن نموذج معقد ويعتبر من أقرب التمثيلات لسطح الكرة الأرضية للمتوسط سطح البحر ويتم الحصول عليه بدمج القياسات الأرضية والأقمار الصناعية لقيم الجاذبية الأرضية. لا يستخدم هذا النموذج في إسقاط الخرائط نظراً لتعقيده وإنما يستخدم في تطبيقات التحكم والمعلومات الجغرافية. يستخدم نموذج جيود في إنشاء "المدخل البياني" "datum" عن طريق إضافة لا انتظام في شكل التمثيل القطعي الناقصي لإضفاء تماثل أكبر مع السطح الحقيقي للأرض حيث يأخذ في عين الاعتبار المعالم الكبيرة التي تضفي قيم أعلى لحقل الجاذبية الأرضية بالإضافة إلى قيم الجاذبية للمعالم الجغرافية الكبيرة مثل السلاسل الجبلية والصفائح التكتونية والسهول.
التصنيف
إن التصنيف الأساسي للمساقط يعتمد على نوع سطح الاسقاط الذي يتم اسقاط الكرة الأرضية عليه. يتم وصف الاسقاط عن طريق وضع سطح عملاق بالتماس مع الأرض، متبوعاً بعملية تحجيم. هذه السطوح تكون إما إسطوانية، مخروطية، أو سمتي، أومستوية. إلا أن الإسقاطات الرياضية لا يمكن تصنيفها بشكل كامل ضمن هذه الأشكال ببساطة. لذلك تم اقتراح عدد آخر من التصانيف في المنشورات الرياضية مثل المخروطي الزائف (تكون خطوط الطول أقواس من دائرة)، الاسطواني الزائف (تكون خطوط الطول خطوطاً مستقيمة) سمتي زائفة أو سمتي رجعي أو مخروطي متعدد.
هناك طريقة أخرى لتصنيف المساقط بالاعتماد على الخصائص التي يحافظ عليها النموذج. بعض أشهر هذه التصانيف هو:
- المحافظة على الاتجاه (سمتياً)
- المحافظة على الأشكال محلياً (بشكل مطلق أو إسقاطي)
- المحافظة على المساحة (تطابق المساحة أو مكافئ المساحة)
- المحافظة على المسافة (مسافة متساوية)
- المحافظة على أقصر طريق.
على اعتبار أن السطح الكروي ليس بسطح قابل قابل للنشر فإنه من المستحيل تحقيق إسقاط للخريطة يحافظ فيه على الأشكال والمساحات في آن واحد.
الاسقاط بالسطح
الاسقاط الاسطواني
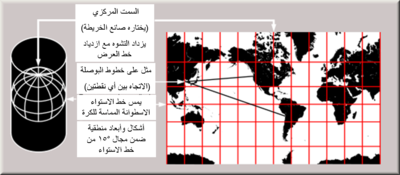
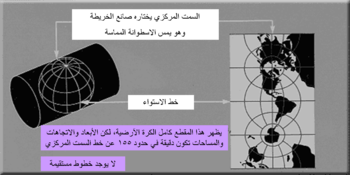
يطلق اسم "الاسقاط الاسطواني" على أي اسقاط تكون فيه خطوط الطول ممثلة بشكل خطوط طولية بينها مسافات متساوية، وخطوط العرض ممثلة على شكل خطوط أفقية.
من الممكن تصوير إسقاط خطوط الطول إلى خطوط طولية بتصور وجود إسطوانة تلف الكرة الأرضية وإسقاط خطوط الطول على هذه الاسطوانة وأخيراً نشر الاسطوانة إلى مستوي. وبسبب شكل الإنشاء لهذا المسقط فإن الاسقطا الأسطواني يقوم بتمديد المسافات شرقاً وغرباً. وتكون قيمة التمديد هذه متساوية عند أي خط عرض في كافة الاسقاطات الأسطوانية. يتم تمييز الاسقاطات الأسطوانية المختلفة بالتمدد الشمالي الجنوبي:
- قيمة التمدد الشمالي-الجنوبي تعادل قيمة التمدد الشرقي الغربي، في هذه الحالة تكون قيمة التحجيم الشرقي-الغربي تعادل قيمة التحجيم الشمالي الجنوبي. هذا الإسقاط يشوه المساحات في اتجاه خطوط الطول.
- قيمة التمدد الشمالي-الجنوبي تزداد باطراد مع زيادة خط العرض، وأسرع بكثير من زيادة التمدد الشرقي-الغربي. هذا الاسقاط غير مناسب لأن نسبة التشوه أسوأ من الحالة السابقة
- يزداد التمدد الشمالي-الجنوبي بزيادة خط العرض، ولكن أبطأ من زيادة التمدد الشرقي-الغربي مثلما يحدث في إسقاط ميلر الاسطواني
- المسافات الشمالية-جنوبية ليست ممدة أو مقلصة، يطلق على هذا اسم الاسقاط الاسطواني المتعادل أو صفيحة كاريه.
- التقلص الشمالي-الجنوبي يعادل التمدد الشرقي-الغربي تبادلياً: يعطي إسقاط اسطواني ذو مساحات متساوية ويأخذ العديد من الأسماء مثل إسقاط غال-بيتر Gall-Peters أو إسقاط بيرمان Behrmann أو إسقاط لامبرت الإسطواني متساوي المساحة lambert cylindrical equa;-area.
انظر أيضاً
- خريطة
- علم الخرائط
- نظام المعلومات الجغرافي
- إسقاط عمودي
- اكسونومتري
- إسقاط متوازي
- الأسقاط التمثيلي لثلاثي الأبعاد
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .