حدسية پوانكاريه
| مسائل جوائز الألفية |
|---|
| نظرية التعقيد |
| حدسية هودج |
| حدسية پوانكاريه |
| فرضية ريمان |
| وجود يانگ-ميلز وفجوة الكتلة |
| معادلات ناڤييه-ستوكس |
| حدسية بيرش وسوينرتون-داير |
| عدل |

حدسية بوانكاريه Poincaré conjecture هي مشكلة في الرياضيات، خصوصاً في الطبولوجيا، صاغها العالم الفرنسي هنري پوانكاريه، سنة 1904. وتعتبر أحد أشهر المسائل الرياضية التي استمرت غامضة لمدة قاربت القرن دون برهنة على صحتها، حتى أعلنت دورية العلوم Science في عددها بتاريخ 22-12-2006 [1]أن هذه المسألة تم حلها نهائياً على يد الرياضي الروسي گريگوري پرلمان.
الحدسية تظهر في البعد 3، أما الأبعاد الأخرى فقد تم البرهنة على صحتها:
- البعد 4 بواسطة فريدمان سنة 1982
- البعد 5 بواسطة زيمان سنة 1961
- البعد 6 بواسطة ستالينگ سنة 1962
- البعد من 7 بواسطة سمال سنة 1961
التاريخ
سؤال پوانكاريه
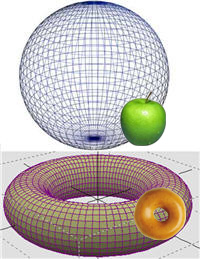
إذا ما مددنا ربطة مطاطة (أستك) حول سطح تفاحة، إذن فبإمكاننا أن نقلص هذا الأستك إلى نقطة بتحريكه ببطء، بدون أن ينقطع وبدون أن نسمح له أن يفارق سطح التفاحة. من ناحية أخرى، لو تخيلنا أن نفس الأستك قد تمدد بطريقة ما في الاتجاه المناسب حول دونت، إذن فلن يكون هناك طريق لانكماشها بعد ذلك لتصبح نقطة بدون قطع إما الأستك أو الدونت. نحن نسمي سطح التفاحة "ببساطة متصل simply connected"، بينما سطح الدونت ليس كذلك. پوانكاريه، قبل نحو مائة عام، عرف أن كرة ثنائية الأبعاد هي في الأساس تتميز بهذه الخاصية "الاتصال البسيط"، ثم طرح السؤال المناظر لكرة ثلاثية الأبعاد (فئة النقاط في فراغ رباعي الأبعاد على بعد وحدة طول من الأصل). اتضح أن هذا السؤال هو في غاية الصعوبة، وقد كافح علماء الرياضيات مع هذا السؤال منذ ذلك الحين.[1]
الاثباتات لمختلف الأبعاد
تحدي اثبات الحدسية كو في الفراغ ثلاثي الأبعاد، أما الأبعاد الأخرى فقد تم البرهنة على صحتها: فالحدسية في الفراغ الرباعي الأبعاد أثبتها فريدمان سنة 1982، وفي الفراغ خماسي الأبعاد أثبتها زيمان سنة 1961، وفي الفراغ سداسي الأبعاد أثبتها ستالينگ سنة 1962، وفي الفراغ السباعي الأبعاد أثبتها سمال سنة 1961.
الوصف الرسمي
في سنة 2000 وبمناسبة السنة العالمية للرياضيات، وضع معهد كلاي للرياضيات (claymath) قائمة بسبع حدسيات رياضية مهمة، ووعد بمنح جائزة مالية قدرها 1,000,000$ لكل من يثبت صحة أو خطأ إحدى هذه الحدسيات، التي أطلق عليها مسائل جوائز الألفية.
والوصف الرسمي لحدسية بوانكاريه هو المترجم أعلاه ويوجد في حدسية بوانكاري
في سنة 2002 بدأ العالم الروسي گريشا پرلمان محاولة لحل المشكلة، وكان يعتبر العالم الأكثر قربا من البرهنة على صحة الحدسية:
5 يونيو 2006: نشرت مجلة «اسيان اوف ماثمتكس» وهي مجلة متخصصة في الرياضيات ومقرها الولايات المتحدة في عددها الاخير ان عالمين صينيين تمكنا من وضع الخطوات النهائية في حل لغز حير العلماء في انحاء العالم منذ أكثر من قرن من الزمان. وذكرت المجلة أن العالمان الاستاذ تشو شي بينغ والاستاذ تساو هواي دونغ قدما اثباتا كاملا للغز بوانكاريه الذي وضعه الفرنسي هنري بونكاريه 1904.
وقال الاستاذ شينغ - تونغ ياو عالم الرياضيات في جامعة هارفارد واحد رؤساء تحرير اسيان جورنال ان الاستاذ تساو هواي دونغ بجامعة ليغ في بنسلفانيا والاستاذ تشو شي بينغ بجامعة صون يات صن في مقاطعة گوانگجو بجنوب الصين وضعا اللمسات الاخيرة للاثبات الكامل لنظرية بوانكاريه الذي حير علماء الرياضيات في انحاء العالم. وتعد نظرية بوانكاريه في الرياضيات خاصة بالطبولوجيا و تعتبر أحد أشهر المسائل الرياضية التي لم يتم برهنتها حتى الآن
برنامج هاملتون وحل پرلمان
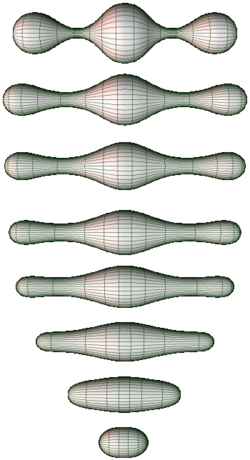
بدأ برنامج هاملتون في ورقة قدمها عام 1982 in which he introduced the Ricci flow on a manifold ووضح كيف يمكن إستخدامها لإثبات بعض الحالات الإستثنائية لحدسية پوانكاريه.[2] وواصل عمله في السنوات التالية، ولكن لم يستطع إثبات الحدسية. ولم يتم التوصل لحل فعلي حتى نشر گريگوري پرلمان أبحاثه مستخدما أفكار من أعمال هاملتون.
في أواخر 2002 و2003 نشر پرلمان ثلاث أوراق بحثية عن arXiv.[3][4][5] وفي هذه الأورق أثبت پرلمان حدسية پوانكاريه وحدسية أكثر عمومية، حدسية ثرستون الهندسية، مكملا برنامج رتشي فلو الذي وُضع مبكرة بواسطة رتشارد هاملتون.
من مايو حتى يوليو 2006، قدمت مجموعات مختلفة أوراق تحتوي على تفاصيل إثبات پرلمان للحدسية پوانكاريه، كالتالي:
- بروس كلاينر وجون و. لوت قدما ورقا عن arXiv في مايو 2006 والتي احتوت على إثبات پرلمان للحدسية الهندسية.[6]
- Huai-Dong Cao and Xi-Ping Zhu نشرا ورقة في عدد يوليو 2006 المجلة الآسيوية للرياضيات، مقدمين إثبات كامل لحدسية پوانكاريه وللحدسيات الهندسية، حيث استعملوا بعض الأعمال المبكرة لكلاينر ولوت .[7]
- مورگان وگنگ تيان قدما ورقة عن arXiv في يوليو 2006، وفيها تفاصيل عن حدسية پوانكاريه (والتي كانت أسهل إلى حد ما عن الحدسية الهندسية الكاملة)[8] and expanded this to a book.[9]
ووجدت المجموعات الثلاثة أن الفجوات في أوراق پرلمان طفيفة ويمكن شغلها باستخدام تقيناته الخاصة.
في 22 أغسطس 2006، منح المؤتمر الدولي للرياضيات (ICM) پرلمان وسام فلدز لعمله على الحدسية، ولكن پرلمان رفض الوسام.[10][11][12] وتحدث جون مورگان للمؤتمر الدولي للرياضايات عن حدسية پوانكاريه، وأعلن في 2006 أن "پرلمان قام بحل الحدسية في عام 2003."[13]
في ديسمبر 2006 كرمت مجلة ساينس إثبات حدسية پوانكاريه كاختراق السنة ووضعتها على غلافها.[14]
الهامش
- ^ [Poincaré Conjecture "http://www.claymath.org/millennium/Poincare_Conjecture/"]. معهد كلاي للرياضيات.
{{cite web}}: Check|url=value (help); External link in|title= - ^ Hamilton, Richard (1982). "Three-manifolds with positive Ricci curvature". Journal of Differential Geometry. 17: 255–306. Reprinted in: Cao, H.D. (2003). Collected Papers on Ricci Flow. International Press. ISBN 978-1571461100.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Perelman, Grigori (2002). "The entropy formula for the Ricci flow and its geometric applications". قالب:Arxiv.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Perelman, Grigori (2003). "Ricci flow with surgery on three-manifolds". قالب:Arxiv.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Perelman, Grigori (2003). "Finite extinction time for the solutions to the Ricci flow on certain three-manifolds". قالب:Arxiv.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Kleiner, Bruce (2006). "Notes on Perelman's Papers". قالب:Arxiv.
{{cite journal}}: Cite journal requires|journal=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Cao, Huai-Dong (2006). "A Complete Proof of the Poincaré and Geometrization Conjectures - application of the Hamilton-Perelman theory of the Ricci flow" (PDF). Asian Journal of Mathematics. 10 (2).
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help); Unknown parameter|month=ignored (help) Erratum. Revised version (December 2006): Cao, Huai-Dong (2006). "Hamilton-Perelman's Proof of the Poincaré Conjecture and the Geometrization Conjecture". قالب:Arxiv.{{cite journal}}: Cite journal requires|journal=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Morgan, John (2006). "Ricci Flow and the Poincaré Conjecture". قالب:Arxiv.
{{cite journal}}: Cite journal requires|journal=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Morgan, John (2007). Ricci Flow and the Poincaré Conjecture. Clay Mathematics Institute. ISBN 0821843281.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Nasar, Sylvia (August 28, 2006). "Manifold destiny". The New Yorker. pp. 44–57.
{{cite news}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) On-line version at the New Yorker website. - ^ Chang, Kenneth (August 22, 2006). "Highest Honor in Mathematics Is Refused". New York Times.
- ^ "Reclusive Russian solves 100-year-old maths problem". China Daily. 23 August 2006. p. 7.
- ^ A Report on the Poincaré Conjecture. Special lecture by John Morgan.
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةscience
وصلات خارجية
- The Poincaré conjecture described by the Clay Mathematics Institute.
- The Poincaré Conjecture (video) Brief visual overview of the Poincaré Conjecture, background and solution.
- The Geometry of 3-Manifolds(video) A public lecture on the Poincaré and geometrization conjectures, given by C. McMullen at Harvard in 2006.
- Bruce Kleiner (Yale) and John W. Lott (University of Michigan): "Notes & commentary on Perelman's Ricci flow papers".
- Stephen Ornes, What is The Poincaré Conjecture?, Seed Magazine, 25 August 2006.
- The slides used by Yau in a popular talk on the Poincaré conjecture.
- "The Poincaré Conjecture" - BBC Radio 4 programme In Our Time, 2 November 2006. Contributors June Barrow-Green, Lecturer in the History of Mathematics at the Open University, Ian Stewart, Professor of Mathematics at the University of Warwick, Marcus du Sautoy, Professor of Mathematics at the University of Oxford, and presenter Melvyn Bragg.
- "Solving an Old Math Problem Nets Award, Trouble" - NPR segment, December 26, 2006.
- Nasar, Sylvia (21 August 2006). "Manifold Destiny: A legendary problem and the battle over who solved it". The New Yorker. Retrieved 2006-08-24.
{{cite news}}: Unknown parameter|coauthors=ignored (|author=suggested) (help)