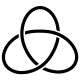
نظرية العقد
في الطبولوجيا، نظرية العقدة knot theory، هي دراسة العقد الرياضية. في حين أنها مستوحاة من العقد التي تظهر في الحياة اليومية، مثل تلك الموجودة في رباط الحذاء والحبل، تختلف العقدة الرياضية من حيث أن الأطراف مرتبطة ببعضها البعض بحيث لا يمكن التراجع عنها، أبسط عقدة هي الحلقة (أو "Unknot"). في اللغة الرياضية، العقدة هي تضمين من دائرة في فضاء إقليدي ثلاثي الأبعاد، R3 (في الطوبولوجيا، لا ترتبط الدائرة بالمفهوم الهندسي الكلاسيكي، ولكن بجميع التشابهات الخاصة بها). عقدتان رياضيتان متساويتان إذا كان من الممكن تحويل إحداهما إلى أخرى عن طريق تشويه R3 على نفسها (المعروف باسم نظير محيط); تتوافق هذه التحولات مع التلاعب في خيط معقود لا يتضمن قطع الخيط أو تمرير الخيط من خلاله.
يمكن وصف العقد بطرق مختلفة. ومع ذلك، فبالنظر إلى طريقة الوصف، قد يكون هناك أكثر من وصف يمثل نفس العقدة. على سبيل المثال، الطريقة الشائعة لوصف العقدة هي رسم تخطيطي مستو يسمى مخطط العقدة. يمكن رسم أي عقدة بعدة طرق مختلفة باستخدام مخطط العقدة. لذلك، فإن المشكلة الأساسية في نظرية العقدة هي تحديد متى يمثل وصفان نفس العقدة.
يوجد حل خوارزمي كامل لهذه المشكلة، والذي لها تعقيد غير معرَّف. من الناحية العملية، غالباً ما يتم تمييز العُقد باستخدام عقدة ثابتة، وهي "الكمية" التي تكون هي نفسها عند حسابها من أوصاف مختلفة للعقدة. تشمل الثوابت المهمة كثيرات حدود العقد ومجموعات العقدة والثوابت الزائدية.
كان الدافع الأصلي لمؤسسي نظرية العقدة هو إنشاء جدول للعقد وروابط، وهي عقدة من عدة مكونات متشابكة مع بعضها البعض. تم جدولة أكثر من ستة مليارات عقدة وروابط منذ بدايات نظرية العقدة في القرن التاسع عشر.
لاكتساب المزيد من الفهم الدقيق، قام علماء الرياضيات بتعميم مفهوم العقدة بعدة طرق. يمكن اعتبار العقد في فضاءات ثلاثية الأبعاد ويمكن استخدام أشياء أخرى غير الدوائر; انظر عقدة (رياضيات). العقدة ذات الأبعاد الأعلى هي الكرات ذات الأبعاد n في الفضاء الإقليدي الأبعاد-m.
التاريخ

اكتشف علماء الآثار أن تقييد العقد يعود إلى عصور ما قبل التاريخ. إلى جانب استخداماتها مثل تسجيل المعلومات وربط الأشياء معاً، فقد اهتم البشر بالعقد لجمالياتها ورموزها الروحية. تظهر العقد في أشكال مختلفة من الأعمال الفنية الصينية التي يعود تاريخها إلى عدة قرون قبل الميلاد (انظر العقد الصينية). تظهر عقدة لا نهاية لها في البوذية التبتية، بينما ظهرت حلقات بورومين بشكل متكرر في ثقافات مختلفة، وغالبًا ما تمثل القوة في الوحدة. فقد أغدق رهبان السلتيك الذين ابتكروا كتاب كِلس بصفحات كاملة مليئة بأعمال عقد سلتيك معقدة.

طُورت النظرية الرياضية للعقد لأول مرة في عام 1771 من قبل ألكسندر تيوفيل ڤاندرموند الذي أشار بوضوح إلى أهمية السمات الطوبولوجية عند مناقشة خصائص العقد المتعلقة بهندسة الموقع. فقد بدأت الدراسات الرياضية للعقد في القرن التاسع عشر مع كارل فريدريش گاوس، الذي عرّف الربط المتكامل (Silver 2006). في ستينيات القرن التاسع عشر، أدت نظرية اللورد كلڤن إلى أن الذرات كانت عقدة في الأثير أدت إلى إنشاء الجداول العقدية الأولى للتصنيف الكامل من قبل پيتر گوثري تيت. نشر تيت، في عام 1885، جدولاً بالعُقَد مع ما يصل إلى عشرة معابر، وما أصبح يُعرف باسم تخمينات تيت. حفز هذا السجل أصحاب نظرية العقدة الأوائل، لكن نظرية العقدة أصبحت في النهاية جزءاً من الموضوع الناشئ للطوبولوجيا.
درس هؤلاء الطوبولوجيون في الجزء الأول من القرن العشرين - ماكس دين، جيمس ألكسندر، وآخرون - العُقد من وجهة نظر مجموعة العقدة والثوابت من التماثل مثل نظرية الإسكندر متعدد الحدود. سيكون هذا هو النهج الرئيسي لنظرية العقدة حتى أدت سلسلة من التقدمات في المعرفة إلى تغيير الموضوع.
في أواخر السبعينيات، أدخل وليام ثورستون الهندسة الزائدية في دراسة العُقد باستخدام نظرية الارتباط المفرط. تم إثبات أن العديد من العقد زائدية، مما يتيح استخدام الهندسة في تحديد عقد ثابتة جديدة وقوية. كشف اكتشاف جونز متعدد الحدود بواسطة ڤوان جونز في 1984 (Sossinsky 2002, pp. 71–89)، والمساهمات اللاحقة من إدوارد ويتن، ماكسيم كونتسڤيتش، وآخرون، كشفوا عن صلات عميقة بين نظرية العقدة والطرق الرياضية في الميكانيكا الإحصائية ونظرية الحقل الكمومي. تم اختراع عدد كبير من ثوابت العقدة منذ ذلك الحين، باستخدام أدوات متطورة مثل مجموعات الكم وتماثل فلوِر.
في العقود العديدة الأخيرة من القرن العشرين، اهتم العلماء بدراسة العقدة الفيزيائية من أجل فهم ظاهرة العقد في DNA والپوليمرات الأخرى. يمكن استخدام نظرية العقدة لتحديد ما إذا كان الجزيء متماكب ("مقابل") أم لا (Flapan 2000). استُخدمت سلاسل التشابك، ذات نهايات مثبتة في مكانها، بشكل فعال في دراسة تأثير توپوإيزوميراز على الحمض النووي (Flapan 2000). قد تكون نظرية العقدة حاسمة في بناء أجهزة الحواسب الكمومية، من خلال نموذج الحوسبة الكمية الطبولوجية (Collins 2006).
تساوي العقدة
تُنشأ العقدة بالبدء بقطعة مستقيمة-أحادية البعد، ولفها حول نفسها بشكل عشوائي، ثم دمج نهايتيها الحرتين معاً لتشكيل حلقة مغلقة (Adams 2004) (Sossinsky 2002). ببساطة، يمكننا أن نقول أن العقدة هي "منحنى بسيط مغلق" أو "منحنى جوردن (المغلق)" (انظر منحنى) - أي: دالة مستمرة ومتباينة "تقريباً" ، مع كون "اللا-تباينية" الوحيدة والتي هي . يعتبر علماء الطبولوجيا أن العقد والتشابكات الأخرى مثل الروابط و الجدائل متكافئة إذا كان من الممكن دفع العقدة بسلاسة، دون تقاطع نفسها، لتتوافق مع عقدة أخرى .
إن فكرة تساوي العقدة هي تقديم تعريف دقيق للزمن الذي يجب فيه اعتبار عقدتين متماثلتين حتى عند وضعهما بشكل مختلف تماماً في الفضاء. التعريف الرياضي الرسمي هو أن العقدة متكافئة إذا كان هناك تشابه مع المحافظة على الاتجاه with .
هناك طريقة أخرى لتعريف معادلة العقدة وهي أن العقدة متكافئة عندما تكون هناك عائلة مستمرة من الأشكال المتماثلة {ht: R3 → R3 لأجل 0 ≤ t ≤ 1} من الفضاء على نفسه، بحيث يحمل الأخير العقدة الأولى في العقدة الثانية. (بشكل أكثر رسمية: تكون العقدتان K1 و K2 متكافئتان إذا كان هناك تعيين مستمر H: R3× [0,1] → R3 such that a) لكل t ∈ [0,1] أخذ التعيين x ∈ R3 إلى H(x,t) ∈ R3 هو تشابه مماثل R3 على نفسها; b) H(x, 0) = x لكل x ∈ R3; and c) H(K1,1) = K2. تُعرف هذه الدالة H باسم نظير محيط.)
يتفق هذان المفهومان لتكافؤ العقدة تماماً على أي العقدة متساوية: عقدة متساوية بموجب تعريف الحفاظ على الاتجاه المتماثل هي أيضاً مساوية ضمن تعريف النظائر المحيطية، لأن أي تشابهات تحافظ على الاتجاه لـ R3 هي المرحلة الأخيرة من النظير المحيط بدءاً من التعريف. على العكس من ذلك، فإن عقدة متكافئة بموجب تعريف النظائر المحيطة متساوية أيضاً في إطار تعريف التماثل الذي يحافظ على الاتجاه، لأن المرحلة t = 1 (النهائية) للنظير المحيط يجب أن تحافظ على الاتجاه وتحمل عقدة واحدة إلى الأخرى.
المشكلة الأساسية في نظرية العقدة، هي مشكلة التعرف، هي تحديد تكافؤ عقدة. توجد خوارزميات لحل هذه المشكلة، مع تقديم ڤولفگانگ هاكن لأول مرة في أواخر الستينيات (Hass 1998). ومع ذلك، يمكن أن تستغرق هذه الخوارزميات وقتاً طويلاً للغاية، وتكمن المشكلة الرئيسية في النظرية في فهم مدى صعوبة هذه المشكلة (Hass 1998). الحالة الخاصة للتعرف على unknot، والتي تسمى مشكلة غير معرفة، والتي لها أهمية خاصة (Hoste 2005). في فبراير 2021، أعلن مارك لاكنبي عن خوارزمية التعرف على العقدة الجديدة التي تعمل في وقت شبه متعدد الحدود.[1]
مخططات العقد
من الطرق المفيدة لتصور العقدة ومعالجتها عرض العقدة على سطح مستو - لنتخيل العقدة التي تلقي بظلالها على الحائط. سيضمن التغيير البسيط في اتجاه الإسقاط أنه واحد لواحد باستثناء النقاط المزدوجة، المسماة تقاطعات، حيث يتقاطع "ظل" العقدة مع نفسه مرة واحدة بشكل عرضي (Rolfsen 1976). في كل تقاطع، حتى تتمكن من إعادة إنشاء العقدة الأصلية، يجب تمييز العقدة الزائدة عن العقدة السفلية. يتم ذلك غالباً عن طريق إحداث فاصل في العقدة السفلية. الرسم البياني الناتج هو منحنى مستوي محاط مع البيانات الإضافية الخاصة بالخيوط المنتهية والتي تحتها عند كل تقاطع. (تسمى هذه المخططات مخططات العقدة عندما تمثل عقدة ومخططات ارتباط وعندما تمثل رابط.) بالمقابل، يمكن ربط الأسطح المعقدة في فضاء-4 بـ سطح محاط في فضاء-3.
الرسم البياني المختزل هو مخطط عقدة لا يوجد فيه تقاطعات قابلة للاختزال (أيضاً تقاطعات لا قيمة لها أو تقاطعات قابلة للإزالة)، أو أُزيلت جميع التقاطعات القابلة للاختزال.(Weisstein, ReducedKnotDiagram) harv error: multiple targets (2×): CITEREFWeisstein (help)(Weisstein, ReducibleCrossing) harv error: multiple targets (2×): CITEREFWeisstein (help) الإسقاط على شكل البتلة هو نوع من الإسقاط حيث تلتقي جميع خيوط العقدة عند نقطة تقاطع واحدة، بدلاً من تشكيل نقاط مزدوجة، وتتصل بها بواسطة حلقات مكونةً "بتلات" غير متداخلة.[2]
حركات رايدماستر
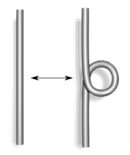
في عام 1927، أظهر العمل بهذا الشكل التخطيطي من العقد، جيمس ألكسندر وگارلاند بيرد برجز، وبشكل مستقل كيرت رايدماستر، أن رسمين تخطيطيين للعقدة ينتميان إلى نفس العقدة يمكن ربطهما بسلسلة من ثلاثة أنواع من الحركات على الرسم البياني، الموضح أدناه. هذه العمليات، التي تسمى الآن "حركات رايدماستر"، هي:
- اللف والفك في أي من الاتجاهين.
- تحريك خصلة واحدة فوق الأخرى تماماً.
- تحريك خصلة فوق التقاطع أو تحته تماماً.
 |

|
| النمط الأول | النمط الثاني |
|---|---|

| |
| النمط الثالث | |
يعتمد الدليل على أن المخططات الخاصة بالعقد المتكافئة مرتبطة بحركات رايدماستر التي تعتمد على تحليل ما يحدث تحت الإسقاط المستوي للحركة التي تأخذ عقدة إلى أخرى. يمكن ترتيب الحركة بحيث يكون الإسقاط في جميع الأوقات تقريباً عبارة عن مخطط عقدة، باستثناء مرات عديدة محدودة عند حدوث "حدث" أو "تقيضه"، كما هو الحال عندما يتقاطع أكثر من خيطين عند نقطة أو خيوط متعددة تصبح مماسة عند نقطة ما. سيظهر الفحص الدقيق أنه يمكن نبذ الأحداث المعقدة، مع ترك أبسط الأحداث فقط: (1) تشكيل "التواء" أو تصحيحه; (2) تصبح خصلتان متماسين عند نقطة ما ويمران عبرها; و(3) ثلاثة خيوط تتقاطع عند نقطة. وهذه هي بالضبط حركات رايدماستر(Sossinsky 2002, ch. 3) (Lickorish 1997, ch. 1).
ثابت العقدة
ثابت العقدة هي "كمية" نفسها للعقد المكافئة (Adams 2004) (Lickorish 1997) (Rolfsen 1976). على سبيل المثال، إذا تم حساب الثابت من مخطط عقدة، فيجب أن يعطي نفس القيمة لمخططين عقدة يمثلان عقدة مكافئة. قد يأخذ الثابت نفس القيمة في عقدتين مختلفتين، لذلك قد لا يكون قادراً في حد ذاته على تمييز كل العقد. الثابت الأساسي هو قابلية التلوين الثلاثي.
تشتمل ثوابت العقدة "الكلاسيكية" على مجموعة العقدة، وهي الزمرة الأساسية من مكمل العقدة، ومتعدد الحدود لألكسندر، والتي يمكن حسابها من ثابت ألكسندر، وحدة مكونة من الغطاء الدوري اللانهائي لمكمل العقدة (Lickorish 1997)(Rolfsen 1976). في أواخر القرن العشرين، تم اكتشاف الثوابت مثل متعدد حدود عقدة "الكم"، ثوابت ڤاسيليڤ والثوابت الزائدية. هذه الثوابت المذكورة أعلاه ليست سوى قمة (نقطة عليا) لنظرية العقدة الحديثة.
تعدد حدود العقد
متعدد حدود العقدة هو ثابت العقدة وهو متعدد الحدود. تشمل الأمثلة المعروفة جونز ومتعددات الحدود الإسكندر. متغير من كثير حدود الإسكندر، متعددالحدود الإسكندر-كونواي، هو متعدد الحدود في المتغير z مع معاملات عدد صحيح (Lickorish 1997).
يُعرّف كثير حدود ألكسندر-كونواي في الواقع من حيث الروابط، والتي تتكون من عقدة واحدة أو أكثر متشابكة مع بعضها البعض. تم شرح المفاهيم أعلاه للعقد، على سبيل المثال الرسوم البيانية وحركات رايدماستر، والتي تحمل الروابط.
لنضع في الاعتبار مخطط ارتباط موجه، أي، يكون فيه كل مكون من مكونات الارتباط وله اتجاه مفضل يشير إليه سهم. للحصول على تقاطع معين في الرسم البياني، لتكن مخططات الارتباط الموجهة الناتجة عن تغيير المخطط كما هو موضح في الشكل:
قد يكون الرسم التخطيطي الأصلي إما أو ، اعتماداً على تكوين التقاطع المختار. ثم يتم تعريف متعدد حدود ألكسندر-كونواي ، بشكل متكرر وفقاً للقواعد:
- (حيث هو أي رسم تخطيطي للحلقة العقدية)
القاعدة الثانية هي ما يشار إليه غالباً باسم skein relation. للتحقق من أن هذه القواعد تعطي ثابتاً للرابط الموجه، يجب على المرء أن يقرر أن كثير الحدود لا يتغير تحت حركات رايدماستر الثلاثة. يمكن تعريف العديد من كثيرات حدود العقدة المهمة بهذه الطريقة.
فيما يلي مثال على حساب نموذجي باستخدام علاقة skein. وهي تحسب كثير حدود الإسكندر-كونواي من عقدة ثلاثية الفصوص. تشير البقع الصفراء إلى مكان تطبيق العلاقة.
تعطي عقدة حلقية ورابط هوف. تطبيق العلاقة على رابط هوف حيث يتم الإشارة إليه،
تعطي رابطاً مشوهاً لواحد مع 0 تقاطعات (إنه في الواقع إلغاء الارتباط لمكونين) وعقدة مفردة. يتطلب فك الارتباط القليل من التسلل:
مما يعني أن C (فك ارتباط مكونين) = 0، نظراً لأن أول كثيرات حدود هي من حلقة مفردة وبالتالي متساوية.
سيظهر وضع كل هذا معاً:
- C(trefoil) = 1 + z(0 + z) = 1 + z2.
نظراً لأن متعدد حدود الإسكندر-كونواي هو ثابت عقدة، فإن هذا يدل على أن ثلاثي الفصيلة لا يعادل العقدة. لذا فالثلاثية الورقية هي حقاً "معقودة".
في الواقع، هناك عقدة ثلاثية الفصوص، تسمى الثلاثية اليمنى واليسرى، وهي صور معكوسة لبعضها البعض (خذ رسماً تخطيطياً للثلاثية الورقية الموضحة أعلاه وقم بتغيير كل تقاطع إلى طريقة أخرى للحصول على الصورة المعكوسة). هذه ليست مكافئة لبعضها البعض، مما يعني أنها ليست amphichiral. تم توضيح ذلك بواسطة Max Dehn، قبل اختراع كثيرات حدود العقدة، باستخدام الطرق النظرية الجماعية (Dehn 1914). لكن كثير حدود ألكسندر-كونواي لكل نوع من العقد الثلاثية ستكون هي نفسها، كما يمكن رؤيته من خلال مراجعة الحساب أعلاه مع صورة المرآة. حيث يمكن لكثير الحدود "جونز" في الواقع التمييز بين عقدة ثلاثية الفصوص اليمنى واليسرى (Lickorish 1997).
الثوابت الزائدية
أثبت وليام ثورستون أن العديد من العقد هي عقد زائدية، مما يعني أن مكمل العقد (أي مجموعة النقاط المكونة من 3 مسافات وليست على العقدة) تقبل بنية هندسية، على وجه الخصوص الهندسة الزائدية. يعتمد الهيكل الزائدي فقط على العقدة، لذا فإن أي كمية محسوبة من البنية الزائدية تكون إذن عقدة ثابتة (Adams 2004).
تتيح لنا الهندسة تصور الشكل الداخلي للعقدة أو تكملة الارتباط من خلال تخيل أشعة الضوء أثناء انتقالها على طول الجيوديسيا في الهندسة. يتم توفير مثال من خلال صورة تكملة حلقات بورومين. يقوم ساكن مكمل الرابط هذا بعرض المساحة بالقرب من المكون الأحمر. الكرات الموجودة في الصورة هي مناظر من horoball لمكونات الارتباط. من خلال تثخين الرابط بطريقة قياسية، يتم الحصول على Horoball لمكونات الارتباط. على الرغم من أن حدود المجاور عبارة عن مستدير، عند النظر إليها من داخل مكمل الرابط، فإنها تبدو وكأنها كرة. يظهر كل مكون رابط على شكل عدد لا نهائي من المجالات (من لون واحد) حيث يوجد عدد لا نهائي من أشعة الضوء من المراقب إلى مكمل الرابط. يكون متوازي الأضلاع الأساسي (المشار إليه في الصورة)، عبارة عن مستطيل ويوضح كيفية تمديد نمط الكرات إلى ما لا نهاية.
هذا النمط ، نمط horoball، هو في حد ذاته ثابت مساعد. تشمل الثوابت الزائدية الأخرى شكل متوازي الأضلاع الأساسي وطول أقصر جيوديسياً وحجماً. وقد استفادت جهود جدولة العقدة والارتباط الحديثة من هذه الثوابت بشكل فعال. تجعل أجهزة الحواسب السريعة والأساليب الذكية للحصول على هذه الثوابت من حساب هذه الثوابت، في الممارسة العملية، مهمة بسيطة(Adams, Hildebrand & Weeks 1991).
الحدود العليا
يمكن فك عقدة ثلاثية الأبعاد عند وضعها في فضاء رباعي الأبعاد. يتم ذلك عن طريق تغيير المعابر. افترض أن خصلة واحدة خلف الأخرى كما تراه من نقطة مختارة. لنرفعه إلى البعد الرابع، لذلك لا يوجد أي عائق (الخيط الأمامي ليس به مكون هناك); ثم نحركه للأمام، ثم نفلته للخلف، والآن في المقدمة. يمكن أن تكون عمليات القياس الخاصة بالمستوى هي رفع خيط عن السطح، أو إزالة نقطة من داخل دائرة.
في الواقع، في أربعة أبعاد، أي حلقة مغلقة غير متقاطعة من سلسلة أحادية البعد تعادل عقدة. أولاً "لندفع" الحلقة إلى فضاء جزئي ثلاثي الأبعاد، وهو أمر ممكن دائماً، على الرغم من أنه تقني للشرح.
كرات تعقيد الأبعاد العليا
نظراً لأن العقدة يمكن اعتبارها طوبولوجيًا كرة ذات بعد واحد، فإن التعميم التالي هو النظر في كرة ثنائية الأبعاد (S2) مضمنة في الفضاء الإقليدي-4 الأبعاد (R4). يكون مثل هذا التضمين معقوداً إذا لم يكن هناك تشابه من R4 على نفسه مع أخذ الكرة الثنائية المضمنة إلى التضمين "الدائري" القياسي للكرة-2. فالعقد المعلقة والعقد المغزولة هما عائلتان نموذجيتان من هذه العقدة ثنائية الكرات.
يشير الأسلوب الرياضي المسمى "الموضع العام" إلى أنه بالنسبة إلى كرة-n في الفضاء الإقليدي ذي الأبعاد-m، إذا كانت m كبيرة بدرجة كافية (اعتماداً على n)، يجب أن تكون الكرة غير معقودة. بشكل عام، تشكل كرات-n متعدد الطيات خطي عقدة فقط في فراغ ذي أبعاد (n + 2)(Zeeman 1963)، على الرغم من أن هذا لم يعد مطلوباً للمجالات الكروية بسلاسة. في الواقع، هناك كرات معقودة بسلاسة في كرات-(4k − 1) في مساحة أبعاد-6k، على سبيل المثال هناك كرة ثلاثية معقودة بسلاسة في {R6 (Haefliger 1962){{Harv|Levine|1965}. وبالتالي، يمكن أن يكون codimension العقدة الملساء كبيراً بشكل عشوائي عند عدم تحديد أبعاد الكرة المعقدة; ومع ذلك، أي كرة-k سلسة مضمنة في Rn with 2n − 3k − 3 > 0 غير معقود. مفهوم العقدة له تعميمات أخرى في الرياضيات، انظر: عقدة (رياضيات)، isotopy classification of embeddings.
كل عقدة في Sn هي رابط مجموعة جبرية حقيقية مع تفرد معزول في Rn+1 (Akbulut & King 1981).
تكون العقدة-n منفردة في Sn ومضمنة في Rm. يكون الرابط-n لنسخ- k لـ Snوالمضمنة في Rm، حيث k عدد طبيعي. فقد دُرست كل من الحالتين m = n + 2 و m > n + 2 جيداً. تحتوي الحالة n > 1 على عقد آجلة مختلفة عن حالة n = 1 وهي مجال مهم.[3][4]
إضافة العقد
يمكن إضافة عقدتين عن طريق قص كلتا العقدتين وربط أزواج النهايات. تسمى العملية مجموع العقدة، أو أحياناً المجموع المتصلأو التركيب المكون من عقدين. يمكن تعريف هذا رسمياً على النحو التالي (Adams 2004): ضع في اعتبارك الإسقاط المستوي لكل عقدة وافترض أن هذه الإسقاطات منفصلة. ابحث عن مستطيل في المستوى حيث يكون زوج من الأضلاع المتقابلة أقواس على طول كل عقدة بينما يكون باقي المستطيل منفصلاً عن العقد. لنكوّن عقدة جديدة بحذف الزوج الأول من الضلعين المتقابلين ومحاذاة الزوجين الآخرين من الضلعين المتقابلين. العقدة الناتجة هي مجموع العقد الأصلية. اعتماداً على كيفية القيام بذلك، قد ينتج عن ذلك عقدتان مختلفتان (ولكن ليس أكثر). يمكن القضاء على هذا الغموض في المجموع فيما يتعلق بالعقد على أنها موجهة، أي وجود اتجاه مفضل للتنقل على طول العقدة، وتتطلب أقواس العقد في المجموع يتم توجيهها باستمرار مع الحدود الموجهة للمستطيل.
مجموع العقدة الموجهة هو تبادلي وتجميعية. فالعقدة "أولية" إذا كانت غير بسيطة ولا يمكن كتابتها كمجموع عقدة لعقدتين غير بسيطتين. العقدة التي يمكن كتابتها على هذا النحو هي "مركبة". يوجد تحليل أولي للعقد، مشابه للعدد الأولي والأرقام المركبة (Schubert 1949). بالنسبة للعقد الموجهة، يعد هذا التحليل فريداً أيضاً. يمكن أيضاً إضافة عقدة ذات أبعاد أعلى ولكن هناك بعض الاختلافات. بينما لا يمكنك تكوين العقدة في ثلاثة أبعاد بإضافة عقدة غير تافهة، يمكنك ذلك في أبعاد أعلى، على الأقل عندما يفكر المرء في العقد الملساء في الترميز 3 على الأقل.
جدولة العقد
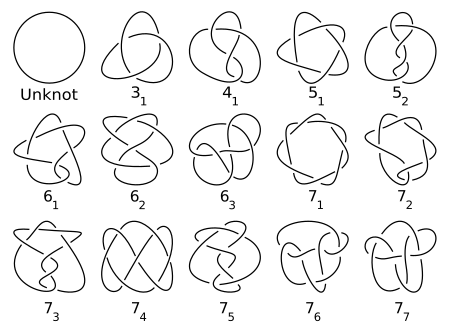
تقليدياً، تم جدولة العقد من حيث رقم التقاطع. تتضمن جداول العقدة بشكل عام العقد الأولية فقط، وإدخال واحد فقط للعقدة وصورة معكوسة (حتى لو كانت مختلفة)(Hoste, Thistlethwaite & Weeks 1998). يزداد عدد العقد غير البسيطة لرقم تقاطع معين بسرعة، مما يجعل الجدولة صعبة حسابياً (Hoste 2005, p. 20). نجحت جهود الجدولة في تعداد أكثر من 6 مليارات عقدة وروابط {(Hoste 2005, p. 28). تسلسل عدد العقد الأولية لرقم تقاطع معين، حتى تقاطع الرقم 16، هو 0، 0، 1، 1، 2، 3، 7، 21، 49، 165، 552، 2176، 9988،46972, 253293, 1388705... (المتتالية A002863 في OEIS). على الرغم من أن الحدود العلوية والسفلية الأسية لهذا التسلسل معروفة، إلا أنه لم يتم إثبات أن هذا التسلسل يتزايد بشكل صارم (Adams 2004).
استخدمت جداول العقدة الأولى لتيت ولتل وكركمان مخططات العقدة، على الرغم من أن تيت استخدم أيضاً مقدمة لملاخظات دوكر. تم اختراع رموز مختلفة للعقد مما يسمح بتبويب أكثر كفاءة (Hoste 2005).
حاولت الجداول الأولى سرد جميع العقد التي تتكون من 10 تقاطعات على الأكثر، وجميع العقد المتناوبة لـ 11 تقاطع (Hoste, Thistlethwaite & Weeks 1998). أدى تطور نظرية العقدة بسبب الإسكندر، ورايديمستر، وسيفرت، وآخرين إلى تسهيل مهمة التحقق، ونشر ألكسندر برگز ورايدميستر في أواخر عشرينيات القرن الماضي جداول العقد التي تصل إلى 9 تقاطع بما في ذلك.
أُجري أول تحقق رئيسي لهذا العمل في الستينيات من قبل جون هورتن كونواي، الذي لم يكتفِ بتطوير طريقة جديدة فحسب، بل أيضاً نتعدد الحدود ألكسندر-كونواي (Conway 1970) (Doll & Hoste 1991). تحقق هذا من قائمة العقد التي تضم 11 تقاطع على الأكثر وقائمة جديدة من الروابط حتى 10 تقاطع. وقد وجد كونواي عدداً من الإغفالات ولكن نسخة واحدة فقط في جداول تيت-ليتل; ومع ذلك فقد فاته النسخ المكررة المسماة أزواج پركو، والتي لن يتم ملاحظتها إلا في عام 1974 بواسطة كنث پركو (Perko 1974). سينتشر هذا الخطأ الشهير عندما أضاف دالي رولفسن جدول عقدة في نصه المؤثر، بناءً على عمل كونواي. تحتوي ورقة كونواي عام 1970 عن نظرية العقدة أيضاً على نسخة مطبعية على صفحتها غير المتناوبة المكونة من 11 عقدة وتجاهل 4 أمثلة - 2 تم سردها سابقاً في أطروحة د. لومبارديرو العليا في عام 1968 في جامعة پرنستون واثنتين أخريين تم اكتشافهما لاحقاً بواسطة آلان كاودرون. [انظر Perko (1982), Primality of certain knots, Topology Proceedings] Less famous is the duplicate in his 10 crossing link table: 2.-2.-20.20 is the mirror of 8*-20:-20. [See Perko (2016), Historical highlights of non-cyclic knot theory, J. Knot Theory Ramifications].
في أواخر التسعينيات، قام هوست وثستلثويت وويكس بجدولة جميع العقد من خلال 16 تقاطع(Hoste, Thistlethwaite & Weeks 1998). في عام 2003، قام رانكين وفلينت وشيرمان بجدولة العقد المتناوبة من خلال 22 تقاطع (Hoste 2005).
ترميز ألكسندر-بريگز
وهو التدوين الأكثر تقليدية، ويرجع ذلك إلى ورقة عام 1927 جيمس ألكسندر وگارلاند بريگز وتم تمديدها لاحقاً بواسطة ديل رولفسن في جدول عقده (انظر الصورة أعلاه وقائمة العقد الأولية). ينظم الترميز ببساطة العقد من خلال رقم التقاطع الخاص بهم. يكتب المرء رقم التقاطع برقم منخفض للإشارة إلى ترتيبه بين جميع العقد مع رقم التقاطع هذا. هذا الترتيب عشوائي وبالتالي ليس له أهمية خاصة (على الرغم من أن عقدة الالتواء تأتي بعد عقدة الحلقة في كل عدد من التقاطعات. تتم كتابة الروابط بواسطة رقم التقاطع مع حرف مرتفع للإشارة إلى عدد المكونات ورمز منخفض للإشارة إلى ترتيبها داخل الروابط مع نفس عدد المكونات والتقاطعات. وبالتالي فإن العقدة ثلاثية الفصوص مسجلة 31 ورابط هوف 221.
ترميز داوكر-ثستلثويت
في تدوين داوكر-ثستلثويت، الذي يُطلق عليه أيضاً، تكون العقدة عبارة عن تسلسل محدود من الأعداد الصحيحة الزوجية. يتم إنشاء الأرقام باتباع العقدة وتمييز التقاطعات بأعداد صحيحة متتالية. نظراً لأن كل تقاطع تمت زيارته مرتين، فإن هذا يؤدي إلى تزاوج أعداد صحيحة زوجية مع أعداد صحيحة فردية. يتم إعطاء علامة مناسبة للإشارة إلى التقاطع والتقاطع. على سبيل المثال، في هذا الشكل، يحتوي مخطط العقدة على تقاطعات مسماة بالأزواج (1,6) (3,−12) (5,2) (7,8) (9,−4) and (11,−10). تدوين داوكر-ثستلثويت لهذا التصنيف هو التسلسل: 6, −12, 2, 8, −4, −10. ويحتوي مخطط العقدة على أكثر من تدوين داوكر-ثستلثويت، وهناك غموض مفهوم جيداً عند إعادة بناء عقدة من تدوين داوكر-ثستلثويت.
ترميز كانواي
يعتمد ترميز كانواي للعقد والروابط، الذي يحمل اسم جون هورتون كانواي، على نظرية التشابك (Conway 1970). ميزة هذا الترميز هو أنه يعكس بعض خصائص العقدة أو الارتباط.
يصف الترميز كيفية إنشاء مخطط ربط معين للارتباط. بدايةً بمتعدد السطوح الأساسي، رسم بياني مستو رباعي التكافؤ بدون مناطق مضلع ثنائي. يتم الإشارة إلى متعدد السطوح هذا أولاً بعدد الرؤوس ثم عدد من العلامات النجمية التي تحدد موضع متعدد السطوح في قائمة متعددات الوجوه الأساسية. على سبيل المثال، يشير الرقم 10** إلى متعدد السطوح الثاني ذي 10 رؤوس في قائمة كانواي.
كل رأس له تشابك جبري مستبدل بداخله (كل رأس موجه لذلك لا يوجد اختيار عشوائي في الاستبدال). كل تشابك من هذا القبيل له تدوين يتكون من أرقام و علامات + أو −.
مثال على ذلك هو 1*2 −3 2. يشير الرقم 1* إلى متعدد السطوح الأساسي ذي الرأس الواحد فقط. 2 −3 2 هو تسلسل يصف الكسر المستمر المرتبط بالتشابك المنطقي. يُدرج هذا التشابك عند قمة متعدد السطوح الأساسي 1*.
مثال أكثر تعقيداً هو 8*3.1.2 0.1.1.1.1.1 هنا مرة أخرى يشير 8* إلى متعدد الوجوه الأساسي ذو 8 رؤوس. الفترات تفصل بين الترميز لكل تشابك.
يعترف أي ارتباط بمثل هذا الوصف، ومن الواضح أن هذا تدوين مضغوط للغاية حتى بالنسبة لرقم التقاطع الكبير جداً. هناك بعض الاختصارات الأخرى المستخدمة عادة. عادةً ما يتم كتابة المثال الأخير 8*3:2 0، حيث يتم حذف تلك الأرقام والاحتفاظ بعدد النقاط باستثناء النقاط الموجودة في النهاية. بالنسبة للعقدة الجبرية كما في المثال الأول، غالباً ما يتم حذف 1*.
تسرد الورقة الأولى لكونواي حول الموضوع ما يصل إلى متعدد السطوح الأساسية المكونة من 10 رؤوس والتي يستخدمها لجدولة الروابط، والتي أصبحت قياسية لتلك الروابط. للحصول على قائمة أخرى من متعدد وجوه الرأس الأعلى، وهناك خيارات غير قياسية متاحة.
رمز گاوس
رمز گاوس، على غرار تدوين داوكر، يمثل عقدة مع سلسلة من الأعداد الصحيحة. ومع ذلك، فبدلاً من تمثيل كل معبر برقمين مختلفين، يتم تمييز التقاطعات برقم واحد فقط. عندما يكون التقاطع عبارة عن تجاوز عرضي، يتم سرد رقم موجب. عند التقاطع السفلي، رقم سالب.
على سبيل المثال، يمكن إعطاء عقدة ثلاثية الفصوص في رمز گاوس كـ: 1,−2,3,−1,2,−3
رمز گاوس محدود في قدرته على تحديد العُقد ببضع مشاكل. تعتبر نقطة البداية في العقدة التي يتم عندها البدء في تتبع التقاطعات العشوائية، ولا توجد طريقة لتحديد الاتجاه الذي يجب تتبعه. أيضاً، لا يستطيع رمز گاوس الإشارة إلى سيطرة كل تقاطع، وهو أمر ضروري لتحديد العقدة مقابل عكسها. على سبيل المثال، لا يحدد كود گاوس الخاص بالعقدة الثلاثية ما إذا كانت ثلاثية الفصوص اليمنى أو اليسرى.
غالباً ما يتم حل هذه المشكلة الأخيرة باستخدام رمز گاوس الموسع. في هذا التعديل، يتم اختيار علامة الموجب/السالب في المثال الثاني من كل رقم لتمثيل تسليم هذا التقاطع، بدلاً من علامة أعلى/أسفل للتقاطع، وهو ما يتم توضيحه في الحالة الأولى من الرقم. يتم إعطاء التقاطع الأيمن رقماً موجباً، ويتم إعطاء التقاطع الأيسر رقماً سالباً.
انظر أيضاً
- Contact geometry#Legendrian submanifolds and knots
- العقد والمخططات
- قائمة موضوعات نظرية العقدة
- عقدة جزيئية
- عقد كمومية
- طبولوجيا كمومية
- نظرية الشريط
- أنواع العقد
المصادر
- Adams, Colin (2004), The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, American Mathematical Society, ISBN 978-0-8218-3678-1
- Adams, Colin; Hildebrand, Martin; Weeks, Jeffrey (1991), "Hyperbolic invariants of knots and links", Transactions of the American Mathematical Society 326 (1): 1–56, doi:
- Akbulut, Selman; King, Henry C. (1981), "All knots are algebraic", Comm. Math. Helv. 56 (3): 339–351, doi:
- Bar-Natan, Dror (1995), "On the Vassiliev knot invariants", Topology 34 (2): 423–472, doi:
- Collins, Graham (April 2006), "Computing with Quantum Knots", Scientific American 294 (4): 56–63, doi:, Bibcode: 2006SciAm.294d..56C
- Dehn, Max (1914), "Die beiden Kleeblattschlingen", Mathematische Annalen 75: 402–413
- Conway, John Horton (1970), "An enumeration of knots and links, and some of their algebraic properties", Computational Problems in Abstract Algebra, Pergamon, pp. 329–358, ISBN 978-0080129754, OCLC 322649
- Doll, Helmut; Hoste, Jim (1991), "A tabulation of oriented links. With microfiche supplement", Math. Comp. 57 (196): 747–761, doi:, Bibcode: 1991MaCom..57..747D
- Flapan, Erica (2000), "When topology meets chemistry: A topological look at molecular chirality", Outlooks (Cambridge University Press), ISBN 978-0-521-66254-3, https://books.google.com/books?id=sh3uWYLfozsC
- Haefliger, André (1962), "Knotted (4k − 1)-spheres in 6k-space", Annals of Mathematics, Second Series 75 (3): 452–466, doi:
- Hass, Joel (1998), "Algorithms for recognizing knots and 3-manifolds", Chaos, Solitons and Fractals 9 (4–5): 569–581, doi:, Bibcode: 1998CSF.....9..569H
- Hoste, Jim; Thistlethwaite, Morwen; Weeks, Jeffrey (1998), "The First 1,701,935 Knots", Math. Intelligencer 20 (4): 33–48, doi:
- Hoste, Jim (2005), "The enumeration and classification of knots and links", Handbook of Knot Theory, Amsterdam: Elsevier, http://pzacad.pitzer.edu/~jhoste/HosteWebPages/downloads/Enumeration.pdf
- Levine, Jerome (1965), "A classification of differentiable knots", Annals of Mathematics, Second Series 1982 (1): 15–50, doi:
- Kontsevich, Maxim (1993), "Vassiliev's knot invariants", I. M. Gelfand Seminar, Adv. Soviet Math., 2 (Providence, RI: American Mathematical Society) 16: 137–150, doi:, ISBN 9780821841174
- Lickorish, W. B. Raymond (1997), An Introduction to Knot Theory, Graduate Texts in Mathematics, Springer-Verlag, ISBN 978-0-387-98254-0, https://books.google.com/books?id=PhHhw_kRvewC
- Perko, Kenneth (1974), "On the classification of knots", Proceedings of the American Mathematical Society 45 (2): 262–6, doi:
- Rolfsen, Dale (1976), Knots and Links, Mathematics Lecture Series, 7, Berkeley, California: Publish or Perish, ISBN 978-0-914098-16-4, https://books.google.com/books?id=naYJBAAAQBAJ
- Schubert, Horst (1949), "Die eindeutige Zerlegbarkeit eines Knotens in Primknoten", Heidelberger Akad. Wiss. Math.-Nat. Kl. (3): 57–104
- Silver, Dan (2006), "Knot theory's odd origins", American Scientist 94 (2): 158–165, doi:, http://www.southalabama.edu/mathstat/personal_pages/silver/scottish.pdf
- Simon, Jonathan (1986), "Topological chirality of certain molecules", Topology 25 (2): 229–235, doi:
- Sossinsky, Alexei (2002), Knots, mathematics with a twist, Harvard University Press, ISBN 978-0-674-00944-8
- Turaev, V. G. (1994), "Quantum invariants of knots and 3-manifolds", De Gruyter Studies in Mathematics (Berlin: Walter de Gruyter & Co.) 18, ISBN 978-3-11-013704-0
- Weisstein, Eric W. "Reduced Knot Diagram". MathWorld. Wolfram. Retrieved 8 May 2013.
{{cite web}}: Invalid|ref=harv(help) - Weisstein, Eric W. "Reducible Crossing". MathWorld. Wolfram. Retrieved 8 May 2013.
{{cite web}}: Invalid|ref=harv(help) - Witten, Edward (1989), "Quantum field theory and the Jones polynomial", Comm. Math. Phys. 121 (3): 351–399, doi:, Bibcode: 1989CMaPh.121..351W
- Zeeman, E. C. (1963), "Unknotting combinatorial balls", Annals of Mathematics, Second Series 78 (3): 501–526, doi:
- ^ Marc Lackenby announces a new unknot recognition algorithm that runs in quasi-polynomial time, Mathematical Institute, University of Oxford, 2021-02-03, https://www.maths.ox.ac.uk/node/38304, retrieved on 2021-02-03
- ^ Adams et al. 2015.
- ^ Levine, J.; Orr, K (2000), "A survey of applications of surgery to knot and link theory", Surveys on Surgery Theory: Papers Dedicated to C.T.C. Wall, Annals of mathematics studies, 1, Princeton University Press, ISBN 978-0691049380 — An introductory article to high dimensional knots and links for the advanced readers
- ^ Ogasa, Eiji (2013), Introduction to high dimensional knots, Bibcode: 2013arXiv1304.6053O — An introductory article to high dimensional knots and links for the beginners
قراءات إضافية
كتب تمهيدية
There are a number of introductions to knot theory. A classical introduction for graduate students or advanced undergraduates is (Rolfsen 1976). Other good texts from the references are (Adams 2001) and (Lickorish 1997). Adams is informal and accessible for the most part to high schoolers. Lickorish is a rigorous introduction for graduate students, covering a nice mix of classical and modern topics.
- Burde, Gerhard; Zieschang, Heiner (1985), Knots, De Gruyter Studies in Mathematics, 5, Walter de Gruyter, ISBN 978-3-11-008675-1, https://books.google.com/books?id=DJHI7DpgIbIC
- Crowell, Richard H.; Fox, Ralph (1977). Introduction to Knot Theory. ISBN 978-0-387-90272-2.
- Kauffman, Louis H. (1987), On Knots, ISBN 978-0-691-08435-0, https://books.google.com/books?id=BLvGkIY8YzwC
- Kauffman, Louis H. (2013), Knots and Physics (4th ed.), World Scientific, ISBN 978-981-4383-00-4, https://books.google.com/books?id=fSKrRQ77FMkC
مسوحات
- Menasco, William W.; Thistlethwaite, Morwen, eds. (2005), Handbook of Knot Theory, Elsevier, ISBN 978-0-444-51452-3
- Menasco and Thistlethwaite's handbook surveys a mix of topics relevant to current research trends in a manner accessible to advanced undergraduates but of interest to professional researchers.
- Livio, Mario (2009), "Ch. 8: Unreasonable Effectiveness?", Is God a Mathematician?, Simon & Schuster, pp. 203–218, ISBN 978-0-7432-9405-8
وصلات خارجية
- "Mathematics and Knots" This is an online version of an exhibition developed for the 1989 Royal Society "PopMath RoadShow". Its aim was to use knots to present methods of mathematics to the general public.
التاريخ
- Thomson, Sir William (1867), "On Vortex Atoms", Proceedings of the Royal Society of Edinburgh VI: 94–105, http://zapatopi.net/kelvin/papers/on_vortex_atoms.html
- Silliman, Robert H. (December 1963), "William Thomson: Smoke Rings and Nineteenth-Century Atomism", Isis 54 (4): 461–474, doi:
- Movie of a modern recreation of Tait's smoke ring experiment
- History of knot theory (on the home page of Andrew Ranicki)
جداول وبرمجيات العقد
- KnotInfo: Table of Knot Invariants and Knot Theory Resources
- The Knot Atlas — detailed info on individual knots in knot tables
- KnotPlot — software to investigate geometric properties of knots
- Knotscape — software to create images of knots
- Knoutilus — online database and image generator of knots
- KnotData.html — Wolfram Mathematica function for investigating knots





![{\displaystyle K\colon [0,1]\to \mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3527c328346ff511b17bd2fe2ae5f3504df3d2e9)