جاذبية
| ميكانيكا كلاسيكية | ||||||||
تاريخ...
| ||||||||
الجاذبية أو الثقالة Gravity هي ميل الكتل والأجسام للتحرك والانجذاب نحو بعضها البعض كما في الجاذبية بين المغناطيس والأجسام الحديدية، ولقد كان إسحاق نيوتن أول من تحدث عن قوى الجاذبية (الثقالة) محاولا وضع نظرية تفسر ميل الأجسام للسقوط نحو الأرض (تفاحة نيوتن) بشكل يتناسق مع قوانينه الثلاثة للحركة .
فالوزن هو القوة التي تحثها الجاذبية محدثة الانجذاب بين الأرض والجسم المعني وهي تساوي جداء تسارع الجاذبية في كتلة الجسم. وكان أول من وضع نظرية للجاذبية هو الفبزبائي المعروف أسحاق نيوتن وبقيت هذه النظرية صامدة حتى تم استبدالها من قبل آينشتاين بنظرية النسبية العامة لكن معادلة نيوتن تبقى صحيحة وأكثر عملية عندما نتحدث عن حقول جاذبية ضعيفة كإرسال المركبات الفضائية والتطبيقات الهندسية الانشائية مثل بناء الجسور المعلقة.
انتشر مصطلح الجاذبية الأرضية مبكرا كون فكرة التجاذب كانت راسخة حسب النظرة النيوتنية، لاحقاً انتشر مصطلحي الجاذبية كتعميم لظاهرة التجاذب بين أي جسمين، و مصطلح ثقالة المشتق من الثقل وهو أكثر دلالة على مفهوم النظرية النسبية للثقالة حيث تعتبر النسبية الثقالة أو الجاذبية مجرد التواء في الزمكان وليس هناك من أي تجاذب بين الأجسام. بشكل عام قد يكون من الأنسب استخدام مصطلح "جاذبية" في إطار الميكانيكا الكلاسيكية في حين يستخدم مصطلح "ثقالة" في إطار النظرية النسبية.
تدل التجربة على أن النسبة بين ثقليْ جسمين إذا قيسا في المكان نفسه لا تتوقف على موضع هذا المكان، ويشار إلى ذلك بالقول إن ثقل أي جسم في أي مكان يتناسب مع مقدارٍ مستقل عن المكان، اصطُلح على تسميته كتلة الجسم الثقالية وعلى الرمز إليه بالحرف ك. أما ثابت التناسب، أي النسبة بين ثقل الجسم ث وكتلته ك، فتسمى الثقالة جـ، وهي مقدار يتغير من مكان إلى آخر، ويقدر بالنيوتن لكل كيلوغرام، ويعني هذا أن ، وكتابة هذه العلاقة على النحو ث = ك.ج (1)، تقابل تماماً العلاقة التحريكية التي تُعطي تغير سرعة جسم، أي تسارعه تع، بفعل القوة ق، المؤثرة فيه مع كتلته المسماة الكتلة العطالية inert كَ، وهي العلاقة: ق = كَ تع (2). وهذا يعني أن الجسم الساقط سقوطاً حراً يكتسب تسارعاً مقداره جـ، ومن ثم يُعدُّ جـ تسارع الثقالة في المكان المعيَّن، ويقدَّر حينئذ بالمتر لكل ثانية في الثانية. وقد تبين من تجارب أجريت حديثاً أن: ك = كَ بدقة بلغت رتبة عالية، ورمز إليهما برمز واحد (ك).
وإذا كان الجسم على الأرض ساكناً، فإن قيمة شدة الثقالة جـ لا تعود إلى قوة واحدة بل إلى قوتين، أولاهما، التي تؤلف القسم الأساسي، هي قوة الجذب النيوتني المعطاة بالعلاقة:
حيث ج ثابت الجاذبية العام، نق نصف قطر الأرض المتوسط، كـ كتلة الأرض. أما القوة الثانية فهي القوة المركزية النابذة الناجمة عن دوران الأرض حول محورها الجغرافي، وتُعطى عند خط العرض ع بالعلاقة ق= ك سه2 نق ع (4)، حيث سه: السرعة الزاوية، نقع نصف قطر الدوران عند خط العرض ع.
وعلى الرغم من أن هاتين العبارتين مختلفتان اختلافاً كبيراً. فإنهما تتناسبان طرداً مع القيمة الوحيدة المقبولة للكتلة ك، وهذا يتيح التركيب المتجهي للشدتين الموافقتين، ويعطى اتجاه الشاقول في مكانٍ ما باتجاه الثقالة.
وتتزايد قيمة القوة المركزية النابذة من الصفر عند القطبين حتى 3.385سم/ثا2 عند خط الاستواء. وقد أطلق على الوحدة سم/ثا2 الاسم غال تكريماً للعالم غاليليو. ومن الأسباب التي تؤدي إلى تغير قيمة جـ مع خط العرض إضافة إلى القوة المركزية، وهي الكبرى أثراً، البعد عن مركز الأرض واختلاف توزع الكتل في القشرة الأرضية ووجود فلزات أو زيوت أو مواد أخرى كتلتها الحجمية أكبر من الكتلة الحجمية الوسطى للأرض أو أصغر منها.
ثابت الجاذبية
إن تعيين قيمة هذا الثابت الأساسي من ثوابت الفيزياء بالتجربة عملية صعبة ومركبة. ومن العمليات التي اتُّبعت في هذا الشأن تجربة، كان كافنديش Cavendish أول من أجراها (عام 1798)، وتقضي هذه التجربة بقياس الدور الاهتزازي لنواس فتل يتألف من سلك دقيق جداً معلق شاقولياً ويحمل في نهايته السفلى قضيباً صلباً دقيقاً يعلق من منتصفه بالسلك، ويحمل في طرفيه كرتين صغيرتين.
يقاس دور اهتزاز هذا النواس حول سلكه الشاقولي، وهو بعيد قدر الإمكان عن كل تأثير خارجي، ثم يوضع بالقرب من الكُرتين، وفي جهتي القضيب الأفقي، كرتان ثقيلتان كبيرتان مركزاهما في مستوي النوسان الأفقي. فتعاني كل كُريَّة قوةَ جذب ضعيفة إلى الكرة التي بقربها، ومن ثم تنشأ مزدوجة فتل إضافية، مما يؤدي إلى تغيّر دور نوسان القضيب الأفقي. ومن الفرق بين الدورين تُحسب مزدوجة القوى الإضافية، ثم قوة التجاذب بين كل كرية والكرة التي تقابلها. وبتطبيق قانون نيوتن في الجاذبية على هذه القوة تحسب قيمة الثابت ث.
إن أحسن قيمة مقبولة اليوم لهذا الثابت هي تلك التي قاسها الأمريكيان هيل P.R.Heyl وشرزانوفسكي P.Chrzanovski فوجدا:
إن الارتياب النسبي الكبير هنا لا يفي بالدقة التي يحتاج إليها الفلكيون في الميكانيك السماوي اليوم. والواقع أن الميكانيك السماوي يحتاج إلى الجداء
ثا = ث.ك، حيث ك كتلة الشمس، ويسمى ثابت الجاذبية المركزي الشمسي constante héliocentrique de la gravitation. ويحسب الفلكيون قيمته في جملة وحدات تلائمهم، فيعتمدون كتلة الشمس ك وحدةً للكتل، واليوم (86400 ثانية) وحدةً للزمن، ونصف القطر الكبير لمدار الأرض وحدةً للطول، فيكون:
ثا = 0.01720209895
أما في دراسة حركة القمر والأقمار الصنعية فيحتاجون إلى الثابت ثاَ = ث.كَ، حيث كَ كتلة الأرض. ولدى اعتماد هذه الكتلة وحدةً للكتل وجدوا، من دراسة حركة المسابير sondes القمرية، أن:
قوة الجاذبية
الجاذِبِيَّة قوة الجذب التي تعمل بين جميع الأجسام بسبب كتلتها؛ أي كمية المادة المكونة لها. وبسبب هذه القوة فإن الأجسام التي على الأرض أو بالقرب منها تنجذب إليها. وتسبب قوى الجذب الخاصة بالشمس والقمر إحداث المد والجزر لمياه المحيطات والبحار على الأرض. وتعمل قوى الجذب على أن تظل جزيئات الغازات الساخنة في الشمس متقاربة، وتحافظ على مكان كل كوكب في مداره حول الشمس، وكل نجم في مداره حول مركز المجرة. ويسمى التجاذب الحادث بين جسم والأجسام القريبة منه بقوة الجاذبية. وبالرغم من سهولة ملاحظة تأثيرات الجاذبية فإن تفسير هذه الظاهرة قد حير العلماء لعدة قرون. وقد كان الفيلسوف الإغريقي القديم أرسطو يرى أن الأجسام الثقيلة تسقط أسرع من الخفيفة، وظل هذا الرأي مقبولاً لعدة قرون. ولكن في أوائل القرن السابع عشر الميلادي قدم العالم الإيطالي جاليليو وجهة نظر جديدة عن الجاذبية. وطبقًا لنظريته، فإن جميع الأجسام تسقط بتسارع (معدل تغير السرعة) واحد مالم تعمل مقاومة الهواء أو قوة أخرى على إبطاء سرعة الجسم الساقط. وقد درس الفلكيون القدماء حركة القمر والكواكب. ولكن هذه الحركة لم تُفسر بشكل صحيح إلا في أواخر القرن السابع عشر، عندما أوضح العالم الإنجليزي السير إسحق نيوتن أن هناك ارتباطًا بين القوى الجاذبة للأجسام نحو الأرض وأسلوب حركة الكواكب. بنى نيوتن دراسته على الدراسة الدقيقة لحركة الكواكب، والتي قام بها اثنان من الفلكيين في أواخر القرن السادس عشر الميلادي وأوائل القرن السابع عشر الميلادي، وهما تيخو براهي الدانمركي و يوهانز كيبلر الألماني. فعندما كان نيوتن في الثالثة والعشرين من عمره، أثار سقوط تفاحة سؤالاً في ذهنه عن مدى قوة الجاذبية. وقد تبين له أن نفس قوة الجذب التي سببت سقوط التفاحة هي التي يمكن أن تحافظ على وضع القمر في مداره حول الأرض. ومن القوانين التي اكتشفها كبلر أوضح نيوتن كيف أن قوة الجذب للشمس لا بد أن تقل بزيادة المسافة. وافترض أن قوة جذب الأرض لا بد أن تسلك ذات السلوك، فتمكَّن من حساب القوة التي تجذب القمر إلى الأرض عند سطحها.
انعدام الوزن
ينعدم وزن الشيء عندما يطفو في الماء بتأثير دافعة أرخميدس، ولكن انعدام وزن كائن حيٍ لا يكون حينئذٍ حقيقياً إذ يقتصر تأثيره على انتقاله إلى عضويات الكائن الداخلية بدون أن يُلغي قوى ارتباطها بالعضويات المجاورة لها. فتمارين الغطس في المسابح التي يقوم بها رواد الفضاء لا تحقق إلا انعدام وزن إجمالي يفيد في الألعاب الرياضية الخاصة بالحركات البطيئة لكنها لا تحقق الشروط الفيزيولوجية لانعدامٍ حقيقي للوزن يتطلب أن يطال التأثيرُ كُلَّ نقطةٍ من الكائن؛ ولا يتحقق ذلك إلا عندما تتساوى القوة المركزية النابذة الناجمة عن دوران مركبة فضائية مع جاذبية الأرض في منطقة النهاية الصغرى للجذب الأرضي القمري؛ ويمكن أن يحدث انعدام الوزن لوقت قصيرٍ في حالة سقوط طائرة.
وقد تبين أن رواد الفضاء يعانون، حين يكونون عرضة لانعدام الوزن، اضطراباتٍ فيزيولوجية منها هبوط في معدل ضربات القلب والتنفس، ونقصان مطرد في وزن الجسم وكالسيوم العظام خلال رحلات لمدة وجيزة، ويحدث عكس ذلك بعد العودة إلى الأرض. وقد أُجريت دراسات كيميائية حيوية بينت أن على رائد الفضاء أن يقوم بتدريبات معينة لا تقل عن 40 يوماً، باستعمال أجهزة مصممة تصميماً مناسباً كي يستطيع الرائد أن يحافظ على صحته عند انعدام وزنه.
نظرية الجاذبية لنيوتن
 مقالة مفصلة: قانون نيوتن للجاذبية العالمية
مقالة مفصلة: قانون نيوتن للجاذبية العالمية
قانون الجذب العام لنيوتن هو قانون إستنباطي كمحاولة لوصف قوى الجاذبية بين الأجسام غير المشحونة, و قد استنبطه نيوتن من خلال مشاهدات فلكية عديدة و بالاستعانة بقوانين كيبلر لحركة الكواكب.
يقول قانون الجاذبية العام لنيوتن : أن كل جسم يجذب جسما آخر في الكون بقوة محمولة على الخط الواصل بين المركزين و شدتها متناسبة طرديًا مع كتلتيهما و عكسيًا مع مربع المسافة بينهما .
- الصورة القياسية لقانون الجذب العام لنيوتن
حيث:
- هي القوة الناتجة عن الجاذبية
- هو ثابت الجذب العام بين الكتل
- هي كتلة الجسيم الأول
- هي كتلة الجسيم الثاني
- هو البعد بين الجسيمين
- الصورة الاتجاهية لقانون الجذب العام لنيوتن
حيث:
- هو متجه القوة التي يؤثر بها الجسيم 1 على الجسيم 2
- هو متجه القوة التي يؤثر بها الجسيم 2 على الجسيم 1
- هو ثابت الجذب العام بين الكتل
- و هما كتلتا الجسيمين على الترتيب
- هو البعد بين الجسيمين (أي مقدار المتجه الذي هو مقدار الفرق بين متجهي موضع الجسيمين)
- هو وحدة متجه للمتجه من 1 إلى 2
هذا القانون مثل معظم قوانين الميكانيكا الكلاسيكية يطبق على الاجسام النقطية (الجسيمات) أما الأجسام الكبيرة ذات الاشكال المختلفة فنعمد إلى تطبيق حسبان التكامل من أجل الحصول على شدة قوة الجاذبية المطبقة عليها .
وعلى هذا، فإن أي كتلة مادية، من بين مجموعة كتل موزعة بأي شكل كان، تعاني لدى تحررها من كل قيد آخر، تسارعاً يتناسب عكسياً مع الكتلة المتحركة. فيقال عن الفضاء المحيط بمجموعة الكتل إنه مسرح حقل تجاذبي.
حظي قانون نيوتن هذا بشواهد تجريبية ذات دقة عالية؛ وقد يكون أهمها ما تبين من أنه يفسر تفسيراً جيداً قوانين كبلر Kepler في الميكانيك السماوي، فهو يتيح مثلاً، تعيين مواقع الكواكب في المنظومة الشمسية بفرق ٍبين الموقع المقيس والموقع المحسوب بوساطته وباستخدام قوانين نيوتن التحريكية، لا يزيد على عُشر ثانية قوسية وعلى مدى عشرات الدورات الكوكبية أو مئاتها، ولم يشذ عن هذا القانون سوى عطارد، وبمقدار أقل الزُّهرة والأرض (وهي كواكب خفيفة أقرب إلى الشمس، وقد أمكن تفسير هذا الشذوذ الضعيف في إطار نظرية النسبية العامة، كما سيُرى بعد قليل).
ثمة شاهد إضافي على عمومية هذا القانون في علم الفلك وهو «الحركة النسبية للنجوم الثنائية» étoiles doubles إذ يدور كل نجم حول رفيقه وفق إهليلج (قطع ناقص) يستجيب لقوانين كبلر، وهي نتيجة لقوانين نيوتن، وهنا أيضاً تشذ عن هذا القانون الثنائية العظيمة الكتلة شذوذاً تفسره نظرية النسبية العامة.[1]
طبيعة قوى الجاذبية حسب النظريات الفيزيائية
تعتبر قوة الجاذبية في الميكانيكا الكلاسيكية قوة مباشرة بعيدة المدى بمعنى أن هذه القوة تستطيع التأثير عن بعد بدون واسطة و يتم تأثيرها بشكل لحظي فأي تغير في موقع أحد الجسمين يرافقه تحول لحظي في الجاذبية بينه و بين الجسم الآخر ، ولكي يفسر اسحاق نيوتن هذه الخاصية عمد إلى تعريف حقل جاذبية كوني موجود في كل نقطة من الفضاء . هذا الحقل هو حقل إتجاهي يعبر عنه بمتجه في كل نقطة و يمثل قوة الجاذبية التي تتعرض لها وحدة الكتل عندما توضع في هذه النقطة .
تنص نظرية النسبية العامة لآينشتاين على أن وجود أي شكل من أشكال المادة أو الطاقة أو العزم يحدث انحناء في الزمكان ، وبسبب هذا الانحناء فان المسارات التي تسلكها الأجسام في الأطر المرجعية القصورية يمكن أن تنحرف أو تغير اتجاهها ضمن الزمن . و هذا الانحراف يظهر لنا على أنه تسارع نحو الاجسام الكبيرة و عرفه نيوتن بأنه ثقالة أو جاذبية . و بالتالي فان النسبية العامة ترى تسارع الجاذبية أو السقوط الحر بأنه حركة قصورية فعليا ( منتظمة ) في حين أن المراقب هو من يتحرك حركة متسارعة ، و هذا ما يعرف ب مبدأ التكافؤ .
القياسات المطلقة للثقالة والقياسات النسبية
| النسبية العامة |
|---|
 |
تعتمد هذه القياسات على مشاهدة اهتزازات النواس وعلى مشاهدة سقوط جسم سقوطاً حراً. ففي حالة النواس يُستخدم نواس بسيط مؤلف من كرة معدنية صغيرة كتلتها (ك) معلقة بخيط غير قابل للمط طولـه ل. فالقـوة التي تحرك النواس باتجـاه الشـاقـول هي:
ق = ل2جـ يه، حيث يه زاوية الخيط مع الشاقول. وتُكسب هذه القوةُ الكتلة ك تسارعاً تع يُعطى عندما تكون يه صغيرة بما يلي:
وتدل هذه العلاقة على أن النواس يهتز بحركة توافقية بسيطة يُعطى دورها (د) بالعلاقة:
، أي أن دور النواس لا يتوقف على مادته، فالنواسات البسيطة التي لها الطول نفسه تكون أدوارها واحدة في المكان الواحد.
لكن لا بد، في حالة النواس البسيط الذي يمكن تحقيقه، من إجراء تصحيحات تتعلق بأبعاد كرة النواس وثقل خيطه، بيد أنه يمكن استعمال نواس مركب مكوّن من جسم صلب يهتز حول محورٍ ما، ومن خاصته أنه إذا تساوى دوْراه (د) حين يهتز حول محورين متوازيين واقعيْن على جانبيْ مركز ثقله وعلى بعديْن مختلفين منه، فإن البعد بين المحورين يكون مساوياً لطول النواس البسيط (ل) المواقت، أي الذي له الدور (د) نفسه. ويوصف هذا النواس المركب بأنه عكوس أو قابل للقلب، ويتضمن سكينيْن متوازيتيْن يُنظَّم وضعاهما حتى يتساوى دوْرا اهتزاز النواس، فيقاس البعد (ل) بينهما وكذلك الدور (د) وتُحسب جـ من العلاقة (6).
وقد استُخدمت أجهزة أيسر استعمالاً تسمى مقاييس الثقالة gravimeters، وهي تعتمد على معادلة ثقل جسم بقوة أخرى مثل قوة نابض مشدود. وما يقاس حينئذ هو الوضع اللازم لإعادة وضع توازن المجموعة المتحركة إلى نقطة ثابتة؛ وتعتمد المسألة كلياً على ثابت قوة النابض. وأكثر ما تُستخدم هذه المقاييس لإيجاد الفروق بين قيم حـ في محطات متتابعة، ويمكن أن تكون دقتها عالية تصل إلى نحو 0.01 ملي غال. وتمتاز هذه الأجهزة بأن القياس بها بسيط وسريع، وأنه يسهل نقلها من مكان إلى آخر، وهذا أتاح إجراء عدد كبير من القياسات في أماكن مختلفة من العالم.
لكن قياس جـ قياساً مباشراً يُنَفَّذُ بمشاهدة سقوط جسم سقوطاً حراً يخضع للقانون:
، حيث س مسافة السقوط، ز مدة السقوط، سر السرعة الابتدائية للجسم. وقد أمكن حديثاً إجراء قياسات دقيقة لمددٍ فاصلة (ز) قصيرة جداً، ومسافات (س) في الوقت نفسه باتباع طريقة عُرف مبدؤها منذ حين.
ففي جهاز المكتب الدولي للمقاييس والموازين يُقذف الجسم من الأسفل إلى الأعلى شاقولياً وهو يحمل مرآة ذات شكل مناسب (موشورية أو مكعبية) ينعكس عنها شعاع ضوئي ليزري شاقولي يتداخل مع شعاع آخر في جهازٍ استُوحي من مقياس ميكلسون التداخلي. وتُقاس المدة (ز) اللازمة لاختفاء الأهداب باستعمال مضاعف فوتوني. وتصل دقة قياس جـ بهذه الطريقة التداخلية إلى 0.01 ملي غال، ويمكن إعادة التجربة على نحو متصلٍ تقريباً.
وقد أُجريت هذه القياسات المطلقة للثقالة في أماكن مختلفة من سطح الأرض وأمكن تحديد عددٍ من قيم جـ المرتبطة بمواقع معينة، وقد بلغت الدقة في قياسها ستة أرقام معنوية .
والسبب في أن العلماء يسعون إلى دقة كهذه هو أن معرفة قيمة جـ على سطح الأرض تفيد في تفسير بنية الأرض وشكلها، كما تبين الاختلافات في الكتلة الحجمية للمواد الواقعة تحت سطح الأرض، وهذه تفيد الجيولوجيين في كشف وجود ترسبات النفط والزيوت تحت سطح الأرض. وقد صرفت بعض الشركات مبالغ طائلة لقياس جـ في مناطق مختلفة من سطح الأرض. كذلك فإن الحصول على صيغة دقيقة تُستنتج منها قيم الثقالة جـ في الفضاء لا غنى عنها للتنبؤ بسير المركبات الفضائية.
أما القياسات النسبية فهي سلسلة قياسات أو تسجيلات متواصلة تجري في مكان واحد لدراسة تغيرات قيم جـ بتأثير الأسباب المشوشة المتغيرة مع الزمن، ولا سيما تلك التي تُعزى إلى ظاهرة المد والجزر التجاذبية الناجمة عن جذب الشمس والقمر أو إلى عدم انتظام كثافة الطبقات التي تحت سطح الأرض. وينتج من ذلك انحرافات ضئيلة دورية للشاقول في المكان الذي يجري القياس فيه. وتجري هذه القياسات النسبية باستعمال نواسات لا يتبدل شكلها مثل النواس القابل للقلب العكوس، أو باستعمال أجهزة تكون تشوهاتها ناجمة كلياً عن المرونة.
التاريخ من نظرية الجاذبية
 مقالة مفصلة: تاريخ نظرية الجاذبية
مقالة مفصلة: تاريخ نظرية الجاذبية
الثورة العلمية
لقد بدأ العمل على نظرية الجاذبية الحديقة في أواخر القرن السادس عشر وبداية القرن السابع عشر حيث قام جاليليو بتجربته الشهيرة التي رمى فيها كرات ذات كُتَل مختلفة من أعلى برج بيزا وبيّن ان سرعة وصول الجسم للارض لا يتعلق بكثلة الجسم. لاحقاً قام أيضا بتجربة دحرجة الكرات على سطح مائل واستنتج ان السبب الذي قد يؤدي إلى وصول الاجسام الأثقل للارض قبل الاجسام الاخف في بعض الأحيان هو احتكاك الهواء في الغلاف الجوي.
قانون نيوتون للثقالة
في سنة 1687 نشر عالم الرياضيات الإنجليزي اسحاق نيوتون نظريته الشهيرة ان قوة الثقالة تتعلق بتربيع البعد بين الجسمين. وبكلماته "أستنتجت من هذا أن القوة التي تُبقي الكواكب في مساراتها متعلقة بتربيع البعد بين مركزيهما. من هنا قارنت القوة التي تمسك القمر في مساره بالقوى على سطح الارض ووصلت إلى نتيجة قريبة جدا" [2] قام إسماعيل بوليادوس بنشر نظرية مشابهة تماما 42 سنة قبل اسحاق نيوتون.
النسبية العامة
| النسبية العامة |
|---|
 |
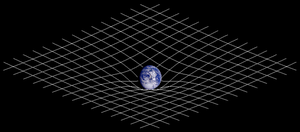
لم يكن أينشتاين يستسيغ فكرة التفاعل عن بعد بين جسمين يفصل بينهما فضاء خالٍ، تلك الفكرة التي يقوم عليها قانون نيوتن في الجاذبية الثقالية. وقد توصل عام 1905 إلى نظريته النسبوية الخاصة التي من أهم سماتها أن ربطت بين المكان (المسافة) والزمان برباط وثيق جعل منهما معاً كائناً فيزيائياً واحداً يُعرف اليوم باسم الزمان ـ المكان (أو الزمكان اختصاراً) وبين المادة والطاقة برباط آخر من شأنه أن يتيح تحول المادة إلى طاقة والعكس.
وفي عام 1915 جاء أينشتاين بنظرية جديدة أخرى تعرف اليوم باسم النسبية العامة. توحي الصورة الرياضية (الرياضياتية) لمعادلات النسبية العامة بأن المادة، أو الطاقة، تؤثر في الزمكان تأثيراً من شأنه أن يجعل الزمكان «متوتراً» أو «منحنيا» كصورة توتر الخيط المطاطي في الفضاء ذي البعد الواحد أو كصورة انحناء السطوح في الفضاء ذي البعدين. وأن من شأن الزمكان أن يؤثر عندئذ بدوره في الأشياء المادية، كائناً فيزيائياً دينامياً (يتأثر بالمادة ويؤثر فيها)، لا كما كان، في ميكانيك نيوتن، مجرد مسرح خامل تقع فيه الأحداث.
ويأخذ التجاذب التثاقلي بين كتلتين ماديتين، في معادلات النسبية العامة، صورة فعل ناجم عن توتر زمكاني تولده الكتلتان في الفضاء المجاور لهما. ثم إن كتلة الشمس تولّد، في الفضاء حولها، زمكاناً منحنياً شبه منغلق بشكل إهليلجات تحيط بالشمس، ومن شأن الكواكب أن تتأثر في حركتها العطالية بهذا الانحناء الزمكاني فتسلك تلك المدارات الإهليلجية.
إن المسارات التي تسلكها الأجسام في الحقل التجاذبي تسمى في علم الرياضيات جيوديزيات géodésiques الفضاء الزمكاني (جيوديزي في فضاء ما هو عموماً أقصر مسافة بين نقطتين من ذلك الفضاء، فهو في السطح المستوي، مثلاً، خط مستقيم بينهما، وعلى سطح الكرة هو قوس الدائرة العظمى بينهما). ومعلوم في النسبية العامة أن الحصول على مسار جسم ما يستدعي حساب جيوديزيات معادلات رياضية تفاضلية من الشكل:
حيث يمثل تفا ل عنصر الطول من [بالخط الجيوديزي]]، ويشير الدليلان ن و هـ بحسب قيمهما (من 1 إلى 4)، إلى إحداثيات الزمكان الأربعة (ثلاثة مكانية، س، ع، ص، وواحد زمني ز). أما المضاريب جن هـ فتتعلق بتوزع الكتل وبحركة مرجع المقارنة، وتتخذ في النسبية العامة شكلاً مختلفاً جداً عن شكلها في ميكانيك نيوتن؛ وهنا يكمن الفرق الجوهري بين النظريتين.
يقود حل هذه المعادلات إلى مسارات مجاورة جداً للمسارات التي يعطيها قانون نيوتن، مع فروق محسوسة في جوار كتل كبيرة جداً. وهذا شأن الكوكب عطارد الخفيف والقريب جداً من الشمس؛ وهنا يتجلى الفرق بحركة دائرية بطيئة يقوم بها أوج مدار الكوكب سرعتُها 43 ثانية قوسية في القرن الواحد؛ أي إن إهليلج المدار غير مغلق تماماً، وهي قيمة تتفق جيداً مع القياسات الرصدية. وهذا المفعول أضعف بكثير في حال الزهرة والأرض بسبب بعديهما الكبيرين عن الشمس، فضلاً عن الكواكب الأخرى التي هي أبعد بكثير عن الشمس.
هذا ومن الجدير أن نلاحظ أن تَعَلُّق تفا ل2 بالكتل وبحركة المرجع معاً يضمن الاستجابة لمبدأ التكافؤ بين المفعولين، الثقالي والعطالي، في الجسم الواحد.
ثم إن من المهم جداً أن يُشار إلى أن الشكل التفاضلي للمعادلة السابقة يدل على أن النسبية العامة هي في الواقع نظرية موضعية locale في الجاذبية، ومن روح هندسية صرفة (تشوه الفضاء الزمكاني)، وقد يحسن أن لا تُستعمل بصددها كلمة «الجاذبية».
الجاذبية وميكانيكا الكم
 مقالات مفصلة: الجاذبية
مقالات مفصلة: الجاذبية - الكم الجاذبية
الجاذبية في الفضاء
 مقالة مفصلة: الجاذبية (علم الفلك)
مقالة مفصلة: الجاذبية (علم الفلك)
الجاذبية هي أكبر معضلة تواجه السفينة الفضائية. والجاذبية تعطي كل الأشياء التي على الأرض أوزانها، وتجعل الأجسام الحرة السقوط تتسارع إلى أسفل. وعلى سطح الأرض يساوي التسارع الناتج عن الجاذبية، والذي يسمى اختصارًا ج، حوالي10م/ الثانية/ الثانية.
ويساعد صاروخ قوي يطلق عليه اسم مركبة الإطلاق المركبة الفضائية على التغلب على الجاذبية. ولكل مركبة إطلاق جزءان أو أكثر، تسمى المراحل. ولابد أن تبذل المرحلة الأولى قوة دافعة تكفي لرفع المركبة الفضائية من على سطح الأرض. ولتقوم المركبة بهذه المهمة بفاعلية، فإن القوة الدافعة للمعزز يجب أن تفوق وزنه. وتزيد القوة الفائضة ـ وهي القوة الدافعة مطروحًا منها وزن المركبة ـ سرعة المركبة الفضائية وترتقي بها في السماء. ويولد المعزز القوة الدافعة بحرق الوقود ونفث غازات إلى خارج المركبة. أما محركات الصاروخ، فتعمل بوقود خاص يسمى الداسر. ويتكون الداسر من وقود سائل أو صلب ممزوج بمؤكسد. والمؤكسد مادة توفر الأكسجين اللازم لحرق الوقود في منطقة انعدام الهواء في الفضاء الخارجي. ويستعمل الأكسجين السائل مؤكسدًا بصفة عامة.
ويطلق على السرعة الدنيا المطلوبة للتغلب على الجاذبية والبقاء في الفضاء السرعة المدارية. وعند درجة تسارع مقدارها 3ج، أي ثلاثة أضعاف تسارع الجاذبية، تصل المركبة لسرعتها المدارية في تسع دقائق. وعند ارتفاع 190كم تساوي السرعة المطلوبة لتحافظ المركبة الفضائية على سرعتها المدارية، وبالتالي البقاء في المدار، حوالي 8كم/ الثانية.
ويطلق على السرعة الدنيا المطلوبة للتغلب على الجاذبية والبقاء في الفضاء السرعة المدارية. وعند درجة تسارع مقدارها 3ج، أي ثلاثة أضعاف تسارع الجاذبية، تصل المركبة لسرعتها المدارية في تسع دقائق. وعند ارتفاع 190كم تساوي السرعة المطلوبة لتحافظ المركبة الفضائية على سرعتها المدارية، وبالتالي البقاء في المدار، حوالي 8كم/ الثانية.
وتسحب شاحنة أو جرار (تراكتور) الصاروخ وحمله الصافي لمنصة الإطلاق، حيث يتم وضعه فوق حفرة من اللهب. ويزود العاملون الصاروخ بالداسر بوساطة أنابيب خاصة.
وعند الإطلاق، تشتعل محركات مرحلة الصاروخ الأولى حتى تفوق قوتها الدافعة وزن الصاروخ. وتجعل القوة الدافعة الصاروخ يرتفع مبتعدًا عن منصة الإطلاق. وإذا كان الصاروخ من النوع الذي يتكون من عدة مراحل، فإن المرحلة الأولى تنفصل عنه بعد استخدام الداسر مباشرة. وتبدأ المرحلة الثانية في الاشتعال لعدة دقائق تنفصل بعدها عند نفاد الداسر. وفي بعض الحالات تبدأ مرحلة الصاروخ العليا الصغيرة في الاحتراق حتى تتحق السرعة المدارية.
وتختلف طريقة إطلاق مكوك الفضاء قليلاً عن باقي المركبات الفضائية. فلمكوك الفضاء معززات صلبة الداسر، بالإضافة إلى محركات الصاروخ الرئيسية التي تحرق الداسر السائل. وتعطي المعززات والمحركات الرئيسية القوة الدافعة اللازمة لانطلاق الصاروخ من منصة الإطلاق. وبعد مرور دقيقتين أو أكثر، تنفصل المعززات من المكوك وتعود للأرض بوساطة مظلة. وتستمر المحركات الرئيسية في الاشتعال حتى يصل المكوك إلى سرعته المدارية. وتساعد محركات صغيرة أخرى المكوك على الوصول إلى سرعته المدارية.
وتعمل المركبة الفضائية على تشغيل صاروخ آخر، يساعدها في الارتقاء إلى ارتفاع أعلى. وعندما تصل المركبة الفضائية إلى سرعة تزيد عن 40% من السرعة المدارية، فإنها تكون قد حققت سرعة الانفلات، وهي السرعة اللازمة لتكون بمنأى عن الجاذبية الأرضية.
إشعاع الجاذبية
 مقالة مفصلة: موجات الجاذبية
مقالة مفصلة: موجات الجاذبية
على شاكلة الموجات الكهرطيسية التي تصدر عن شحنات كهربائية متحركة، تتنبأ معادلات النسبية العامة بأن الكتل المادية المتحركة تفقد قسطاً من طاقتها تحمله موجات تسمى الموجات التجاذبية وتنتشر بسرعة الضوء. وهذه الأمواج، عندما تخترق جملة مادية، تولد اهتزازات عرضانية للمسافات الفاصلة بين الأجسام المادية. ولئن تعذر كشفها حتى الآن في تجارب أرضية، بسبب ضعف سعتها الشديد، فقد تأكد وجودها عن طريق غير مباشر بوساطة عمليات رصد اضطراب حركة بعض النَّبَّاضات الثنائية pulsars binaires.
وهناك اليوم عدة مشروعات في طور التنفيذ تهدف إلى استكشاف أمواج تجاذبية صادرة عن حركات أجرام سماوية كبيرة، كالمجرات، أو عن تفجرها. وفي عام 1958 صُنع كاشف لهذه الموجات يتألف من أسطوانات تهتز بفعل الموجات التجاذبية الآتية من تلك الأجرام اهتزازاً قد لا تتجاوز سعته قطر الذرة، ويُكشف بجهاز تداخل ليزريّ دقيق جداً. وللتيقن من سبب هذا الاهتزاز تُستخدم عدة كواشف متماثلة قد تبلغ المسافات فيما بينها ألف كيلو متر، فتهتز أسطواناتها في وقت واحد وسعة واحدة، إذا كان سببها موجات تجاذبية آتية من خارج الكرة الأرضية. ولئن تم اكتشاف عددٍ لا بأس به من ظواهر ذات ملامح قوية من هذا القبيل، إلا أن هذا الأمر لا يزال بحاجة إلى مزيد من الأرصاد في المشروعات التي تم تنفيذ بعضها وما يزال بعضها الآخر في مرحلة التنفيذ.
العيوب والتناقضات
المصادر
- ^ أدهم السمان. "الجاذبية". الموسوعة العربية.
- ^ *Chandrasekhar, Subrahmanyan (2003). Newton's Principia for the common reader. Oxford: Oxford University Press. (pp.1–2). The quotation comes from a memorandum thought to have been written about 1714.
النظريات البديلة
نظريات بديلة تاريخية
- النظرية الأرسطوطلية للجاذبية
- Le Sage's theory of gravitation (1784) also called LeSage gravity, proposed by Georges-Louis Le Sage, based on a fluid-based explanation where a light gas fills the entire universe.
- Nordström's theory of gravitation (1912, 1913), an early competitor of general relativity.
- Whitehead's theory of gravitation (1922), another early competitor of general relativity.
نظريات بديلة حديثة
- نظرية برانز–ديك للجاذبية (1961)
- الجاذبية المحثوثة (1967), a proposal by Andrei Sakharov according to which general relativity might arise from quantum field theories of matter
- In the modified Newtonian dynamics (MOND) (1981), Mordehai Milgrom proposes a modification of Newton's Second Law of motion for small accelerations
- The self-creation cosmology theory of gravity (1982) by G.A. Barber in which the Brans-Dicke theory is modified to allow mass creation
- Nonsymmetric gravitational theory (NGT) (1994) by جون موفات
- Tensor-vector-scalar gravity (TeVeS) (2004), a relativistic modification of MOND by Jacob Bekenstein
- Gravity as an entropic force, gravity arising as an emergent phenomenon from the thermodynamic concept of entropy.
انظر أيضاً
- Anti-gravity, the idea of neutralizing or repelling gravity
- Artificial gravity
- Escape velocity, the minimum velocity needed to fly away from a massive space object
- g-force, a measure of acceleration
- Gravitational induction
- Gravitational binding energy
- Gravity assist
- Gravity Recovery and Climate Experiment
- Gravity Research Foundation
- قانون گاوس للجاذبية
- Jovian-Plutonian gravitational effect
- قانون كپلر الثالث لحركة الكواكب
- نقطة لاگرانجية
- Mixmaster dynamics
- Newton's laws of motion
- n-body problem
- Pioneer anomaly
- Scalar theories of gravitation
- Speed of gravity
- Standard gravitational parameter
- Standard gravity
- Weightlessness
ملاحظات
- ^ Proposition 75, Theorem 35: p. 956 - I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton's Principia, by I. Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 ISBN 0-520-08817-4
- ^ Max Born (1924), Einstein's Theory of Relativity (The 1962 Dover edition, page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury, Venus, and Earth.)
الهامش
المصادر
- Halliday, David (2001). Physics v. 1. New York: John Wiley & Sons. ISBN 0-471-32057-9.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Serway, Raymond A. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.
قراءات أخرى
- Thorne, Kip S.; Misner, Charles W.; Wheeler, John Archibald (1973). Gravitation. W.H. Freeman. ISBN 0-7167-0344-0.
{{cite book}}: CS1 maint: multiple names: authors list (link)


















