مبرهنة بل

مبرهنة بل Bell's theorem تتألف من مجموعة لاتساويات مترابطة متلائمة مع فرضية الواقعية المحلية ، لكن لا يمكن تطبيقها مع الميكانيك الكمومي .

No physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics.

تبحث المبرهنة أساسا في برهان فون نيومان لبطلان المتغيرات الخفية في تفسير ميكانيك الكم ، و في مفارقة ( أي-بي-آر) EPR paradox .

عندما قدم اينشتاين و بودولسكي و روزن بتقديم مفارقتهم ، فاموا بادخال شك كبير في صحة ميكانيك الكم و جاءت نظرية المتغيرات الخفية لتقدم تفسيرات حول نتائج ميكانيك الكم ، مما يعني أن ميكانيك الكم نظرية غير مكتملة .

أظهر بل أن مفارقة (أي-بي-آر) تحوي افتراضات أساسة حول الواقع تتناقض مع ميكانيك الكم ، و هذه الافتراضات هي أساسا : 1- لا يمكن لأي تأثير أن ينتشر بأسرع من سرعة الضوء ( وهذا شرط أساسي من قوانين المحلية ) . 2- ان احتمالية حدوث أي تغير في أي من المتغيرات الخفية المفترضة هي بين 0% و 100% .

انطلق بل من هنا ليثبت أن هذه الحالة و هذه الشروط لا تنطبق في بعض الحالات مثل مكونات استقطاب السبين في حالة الجسيمات المتشابكة (المترافقة) entangled . فقد كانت النتائج التجريبية لمبرهنة بل متوافقة مع تنبؤات ميكانيك الكم ، بكلام آخر كانت المبرهنة تثبت أن واحدة من فرضيات الواقعية المحلية خاطئة ( اما 1 أو 2 ) .

Example of simple Bell type inequality and its violation in quantum mechanics. Top: assuming any probability distribution among 8 possibilities for values of 3 binary variables ABC, we always get the above inequality. Bottom: example of its violation using quantum Born rule: probability is normalized square of amplitude.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 استعراض

Illustration of Bell test for spin-half particles such as electrons. A source produces a singlet pair, one particle is sent to one location, and the other is sent to another location. A measurement of the entangled property is performed at various angles at each location. The scheme for measurements on photons looks very similar: the quantum state is different but has very similar properties.

Anti-parallel	Pair
	1	2	3	4	…	n
Alice, 0°	+	−	+	+	…	−
Bob, 180°	+	−	+	+	…	−
Correlation	( +1	+1	+1	+1	…	+1 )	/ n = +1
							(100% identical)
Parallel	1	2	3	4	…	n
Alice, 0°	+	−	−	+	…	+
Bob, 0° or 360°	−	+	+	−	…	−
Correlation	( −1	−1	−1	−1	…	−1 )	/ n = −1
							(100% opposite)
Orthogonal	1	2	3	4	…	n
Alice, 0°	+	−	+	−	…	−
Bob, 90° or 270°	−	−	+	+	…	−
Correlation	( −1	+1	+1	−1	…	+1 )	/ n = 0
							(50% identical, 50% opposite)

The best possible local realist imitation (red) for the quantum correlation of two spins in the singlet state (blue), insisting on perfect anti-correlation at 0°, perfect correlation at 180°. Many other possibilities exist for the classical correlation subject to these side conditions, but all are characterized by sharp peaks (and valleys) at 0°, 180°, and 360°, and none has more extreme values (±0.5) at 45°, 135°, 225°, and 315°. These values are marked by stars in the graph, and are the values measured in a standard Bell-CHSH type experiment: QM allows ±1/√2 = ±0.7071…, local realism predicts ±0.5 or less.

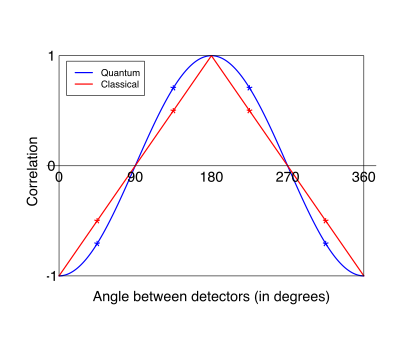
 متباينات بل

Bell inequalities concern measurements made by observers on pairs of particles that have interacted and then separated. Assuming local realism, certain constraints must hold on the relationships between the correlations between subsequent measurements of the particles under various possible measurement settings. Let A and B be as above. Define for the present purposes three correlation functions:

• Let C_e(a, b) denote the experimentally measured correlation defined by

  $C_{e}(a,b)={\frac {N_{++}+N_{--}-N_{+-}-N_{-+}}{N_{++}+N_{--}+N_{+-}+N_{-+}}},$

where N₊₊ is the number of measurements yielding "spin up" in the direction of a measured by Alice (first subscript +) and "spin up" in the direction of b measured by Bob. The other occurrences of N are analogously defined.

• Let C_q(a, b) denote the correlation as predicted by quantum mechanics. This is given by the expression

  $C_{q}(a,b)=\left\langle A\left|({\boldsymbol {\sigma }}\cdot \mathbf {b} )^{(2)}({\boldsymbol {\sigma }}\cdot \mathbf {a} )^{(1)}\right|A\right\rangle ,$

where A is the antisymmetric spin wave function. This value is calculated to be

$C_{q}(a,b)=-\mathbf {a} \cdot \mathbf {b} .$

• Let C_h(a, b) denote the correlation as predicted by any hidden variable theory. In the formalization of above, this is

  $C_{h}(a,b)=E(A(\mathbf {a} ,\lambda )B(\mathbf {b} ,\lambda ))=\int _{\Lambda }A(\mathbf {a} ,\lambda )B(\mathbf {b} ,\lambda )p(\lambda )d\lambda .$

Details on calculation of C_q(a, b)

The two-particle spin space is the tensor product of the two-dimensional spin Hilbert spaces of the individual particles. Each individual space is an irreducible representation space of the rotation group SO(3). The product space decomposes as a direct sum of irreducible representations with definite total spins 0 and 1 of dimensions 1 and 3 respectively. Full details may be found in Clebsch—Gordan decomposition. The total spin zero subspace is spanned by the singlet state in the product space, a vector explicitly given by

$|A\rangle ={\frac {1}{\sqrt {2}}}\left(\alpha ^{(1)}\beta ^{(2)}-\beta ^{(1)}\alpha ^{(2)}\right)={\frac {1}{\sqrt {2}}}\left({\begin{bmatrix}1\\0\end{bmatrix}}\otimes {\begin{bmatrix}0\\1\end{bmatrix}}-{\begin{bmatrix}0\\1\end{bmatrix}}\otimes {\begin{bmatrix}1\\0\end{bmatrix}}\right),$

with adjoint in this representation

$\langle A|={\frac {1}{\sqrt {2}}}\left({\begin{bmatrix}1&0\end{bmatrix}}\otimes {\begin{bmatrix}0&1\end{bmatrix}}-{\begin{bmatrix}0&1\end{bmatrix}}\otimes {\begin{bmatrix}1&0\end{bmatrix}}\right).$

The way single particle operators act on the product space is exemplified below by the example at hand; one defines the tensor product of operators, where the factors are single particle operators, thus if Π, Ω are single particle operators,

$(\Pi \otimes \Omega )(|x\rangle \otimes |y\rangle )=\Pi |x\rangle \otimes \Omega |y\rangle ,$

and

$\Pi ^{(1)}(|x\rangle \otimes |y\rangle )\equiv \Pi |x\rangle \otimes \operatorname {Id} |y\rangle ,$

etc., where the superscript in parentheses indicates on which Hilbert space in the tensor product space the action is intended and the action is defined by the right hand side. The singlet state has total spin 0 as may be verified by application of the operator of total spin J · J = (J₁ + J₂) ⋅ (J₁ + J₂) by a calculation similar to that presented below.

The expectation value of the operator

$\left({\boldsymbol {\sigma }}\cdot \mathbf {b} \right)^{(2)}\left({\boldsymbol {\sigma }}\cdot \mathbf {a} \right)^{(1)}=\left(\operatorname {Id} \otimes {\boldsymbol {\sigma }}\cdot \mathbf {b} \right)\left({\boldsymbol {\sigma }}\cdot \mathbf {a} \otimes \operatorname {Id} \right),$

in the singlet state can be calculated straightforwardly. One has, by definition of the Pauli matrices,

${\boldsymbol {\sigma }}\cdot \mathbf {a} \otimes \operatorname {Id} ={\begin{bmatrix}a_{z}&a_{x}-ia_{y}\\a_{x}+ia_{y}&-a_{z}\end{bmatrix}}\otimes {\begin{bmatrix}1&0\\0&1\end{bmatrix}}.$

Upon left application of this on قالب:Ket one obtains

${\boldsymbol {\sigma }}\cdot \mathbf {a} \otimes \mathrm {Id} |A\rangle ={\frac {1}{\sqrt {2}}}\left({\begin{bmatrix}a_{z}\\a_{x}+ia_{y}\end{bmatrix}}\otimes {\begin{bmatrix}0\\1\end{bmatrix}}-{\begin{bmatrix}a_{x}-ia_{y}\\-a_{z}\end{bmatrix}}\otimes {\begin{bmatrix}1\\0\end{bmatrix}}\right).$

Likewise, application (to the left) of the operator corresponding to b on قالب:Bra yields

$\langle A|\operatorname {Id} \otimes {\boldsymbol {\sigma }}\cdot \mathbf {b} ={\frac {1}{\sqrt {2}}}\left({\begin{bmatrix}1&0\end{bmatrix}}\otimes {\begin{bmatrix}b_{x}+ib_{y}&-b_{z}\end{bmatrix}}-{\begin{bmatrix}0&1\end{bmatrix}}\otimes {\begin{bmatrix}b_{z}&b_{x}-ib_{y}\end{bmatrix}}\right).$

The inner products on the tensor product space is defined by

$\langle x\otimes y|u\otimes v\rangle =\langle x|u\rangle \langle y|v\rangle .$

Given this, the expectation value reduces to

$\langle A|({\boldsymbol {\sigma }}\cdot \mathbf {b} )^{(2)}({\boldsymbol {\sigma }}\cdot \mathbf {a} )^{(1)}|A\rangle =-\mathbf {a} \cdot \mathbf {b} .$

---

With this notation, a concise summary of what follows can be made.

• Theoretically, there exists a, b such that

$C_{q}\neq C_{h},$

whatever are the particular characteristics of the hidden variable theory as long as it abides to the rules of local realism as defined above. That is to say, no local hidden variable theory can make the same predictions as quantum mechanics.

• Experimentally, instances of

$C_{e}\neq C_{h}$

have been found (whatever the hidden variable theory), but

$C_{e}\neq C_{q}\quad {\text{(not found)}}$

has never been found. That is to say, predictions of quantum mechanics have never been falsified by experiment. These experiments include such that can rule out local hidden variable theories. But see below on possible loopholes.

 متباينة بل الأصلية

The inequality that Bell derived can then be written as:

$C_{h}(a,c)-C_{h}(b,a)-C_{h}(b,c)\leq 1,$

where a, b and c refer to three arbitrary settings of the two analysers. This inequality is however restricted in its application to the rather special case in which the outcomes on both sides of the experiment are always exactly anticorrelated whenever the analysers are parallel. The advantage of restricting attention to this special case is the resulting simplicity of the derivation. In experimental work, the inequality is not very useful because it is hard, if not impossible, to create perfect anti-correlation.

This simple form has an intuitive explanation, however. It is equivalent to the following elementary result from probability theory. Consider three (highly correlated, and possibly biased) coin-flips X, Y, and Z, with the property that:

1. X and Y give the same outcome (both heads or both tails) 99% of the time
2. Y and Z also give the same outcome 99% of the time,

then X and Z must also yield the same outcome at least 98% of the time. The number of mismatches between X and Y (1/100) plus the number of mismatches between Y and Z (1/100) are together the maximum possible number of mismatches between X and Z (a simple Boole–Fréchet inequality).

 انظر أيضاً

• Bell test experiments
• Bohr–Einstein debates on quantum mechanics
• CHSH Bell test
• Counterfactual definiteness
• Correlation does not imply causation
• Einstein's thought experiments
• Epistemological Letters
• Free will theorem
• Fundamental Fysiks Group
• GHZ experiment
• Hidden variable theory
• Local hidden variable theory
• Loopholes in Bell test experiments
• Leggett inequality
• Leggett–Garg inequality
• Measurement in quantum mechanics
• Mott problem
• Normally distributed and uncorrelated does not imply independent
• PBR theorem
• Quantum contextuality
• Quantum entanglement
• Quantum nonlocality
• Renninger negative-result experiment
• Sakurai's Bell inequality

 المراجع

• Aspect, A.; et al. (1981). "Experimental Tests of Realistic Local Theories via Bell's Theorem". Phys. Rev. Lett. 47 (7): 460–463. Bibcode:1981PhRvL..47..460A. doi:10.1103/physrevlett.47.460.
• Aspect, A.; et al. (1982). "Experimental Realization of Einstein–Podolsky–Rosen–Bohm Gedankenexperiment: A New Violation of Bell's Inequalities". Phys. Rev. Lett. 49 (2): 91–94. Bibcode:1982PhRvL..49...91A. doi:10.1103/physrevlett.49.91.
• Aspect, A.; et al. (1982). "Experimental Test of Bell's Inequalities Using Time-Varying Analyzers". Phys. Rev. Lett. 49 (25): 1804–1807. Bibcode:1982PhRvL..49.1804A. doi:10.1103/physrevlett.49.1804.
• Aspect, A.; Grangier, P. (1985). "About resonant scattering and other hypothetical effects in the Orsay atomic-cascade experiment tests of Bell inequalities: a discussion and some new experimental data". Lettere al Nuovo Cimento. 43 (8): 345–348. doi:10.1007/bf02746964.
• D'Espagnat, B. (1979). "The Quantum Theory and Reality" (PDF). Scientific American. 241 (5): 158–181. Bibcode:1979SciAm.241e.158D. doi:10.1038/scientificamerican1179-158.
• Bell, J. S. (1966). "On the problem of hidden variables in quantum mechanics". Rev. Mod. Phys. 38 (3): 447–452. Bibcode:1966RvMP...38..447B. doi:10.1103/revmodphys.38.447.
• Bell, J. S. (1964). "On the Einstein Podolsky Rosen Paradox" (PDF). Physics. 1 (3): 195–200.
• J. S. Bell, Introduction to the hidden variable question, Proceedings of the International School of Physics 'Enrico Fermi', Course IL, Foundations of Quantum Mechanics (1971) 171–81
• J. S. Bell, Bertlmann's socks and the nature of reality, Journal de Physique, Colloque C2, suppl. au numero 3, Tome 42 (1981) pp C2 41–61
• J. S. Bell, Speakable and Unspeakable in Quantum Mechanics (Cambridge University Press 1987) [A collection of Bell's papers, including all of the above.]
• Clauser, J. F.; Shimony, A. (1978). "Bell's theorem: experimental tests and implications" (PDF). Reports on Progress in Physics. 41 (12): 1881–1927. Bibcode:1978RPPh...41.1881C. CiteSeerX 10.1.1.482.4728. doi:10.1088/0034-4885/41/12/002.
• Clauser, J. F.; Horne, M. A. (1974). "Experimental consequences of objective local theories". Phys. Rev. D. 10 (2): 526–535. Bibcode:1974PhRvD..10..526C. doi:10.1103/physrevd.10.526.
• Fry, E. S.; Walther, T.; Li, S. (1995). "Proposal for a loophole-free test of the Bell inequalities" (PDF). Phys. Rev. A. 52 (6): 4381–4395. Bibcode:1995PhRvA..52.4381F. doi:10.1103/physreva.52.4381. hdl:1969.1/126533. PMID 9912775.
• E. S. Fry, and T. Walther, Atom based tests of the Bell Inequalities — the legacy of John Bell continues, pp 103–117 of Quantum [Un]speakables, R.A. Bertlmann and A. Zeilinger (eds.) (Springer, Berlin-Heidelberg-New York, 2002)
• R. B. Griffiths, Consistent Quantum Theory', Cambridge University Press (2002).
• Hardy, L. (1993). "Nonlocality for 2 particles without inequalities for almost all entangled states". Physical Review Letters. 71 (11): 1665–1668. Bibcode:1993PhRvL..71.1665H. doi:10.1103/physrevlett.71.1665. PMID 10054467.
• M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press (2000)
• Pearle, P. (1970). "Hidden-Variable Example Based upon Data Rejection". Physical Review D. 2 (8): 1418–25. Bibcode:1970PhRvD...2.1418P. doi:10.1103/physrevd.2.1418.
• A. Peres, Quantum Theory: Concepts and Methods, Kluwer, Dordrecht, 1993.
• P. Pluch, Theory of Quantum Probability, PhD Thesis, University of Klagenfurt, 2006.
• B. C. van Frassen, Quantum Mechanics, Clarendon Press, 1991.
• Rowe, M.A.; Kielpinski, D.; Meyer, V.; Sackett, C.A.; Itano, W.M.; Monroe, C.; Wineland, D.J. (2001). "Experimental violation of Bell's inequalities with efficient detection". Nature. 409 (6822): 791–794. Bibcode:2001Natur.409..791K. doi:10.1038/35057215. PMID 11236986.
• Sulcs, S. (2003). "The Nature of Light and Twentieth Century Experimental Physics". Foundations of Science. 8 (4): 365–391. doi:10.1023/A:1026323203487.
• Gröblacher, S.; et al. (2007). "An experimental test of non-local realism". Nature. 446 (7138): 871–875. arXiv:0704.2529. Bibcode:2007Natur.446..871G. doi:10.1038/nature05677. PMID 17443179.
• Matsukevich, D. N.; Maunz, P.; Moehring, D. L.; Olmschenk, S.; Monroe, C. (2008). "Bell Inequality Violation with Two Remote Atomic Qubits". Phys. Rev. Lett. 100 (15): 150404. arXiv:0801.2184. Bibcode:2008PhRvL.100o0404M. doi:10.1103/physrevlett.100.150404. PMID 18518088.
• The comic Dilbert, by Scott Adams, refers to Bell's Theorem in the 1992-09-21 and 1992-09-22 strips.
• قالب:Cite SEP

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 للاستزادة

The following are intended for general audiences.

• Amir D. Aczel, Entanglement: The greatest mystery in physics (Four Walls Eight Windows, New York, 2001).
• A. Afriat and F. Selleri, The Einstein, Podolsky and Rosen Paradox (Plenum Press, New York and London, 1999)
• J. Baggott, The Meaning of Quantum Theory (Oxford University Press, 1992)
• N. David Mermin, "Is the moon there when nobody looks? Reality and the quantum theory", in Physics Today, April 1985, pp. 38–47.
• Louisa Gilder, The Age of Entanglement: When Quantum Physics Was Reborn (New York: Alfred A. Knopf, 2008)
• Brian Greene, The Fabric of the Cosmos (Vintage, 2004, ISBN 0-375-72720-5)
• Nick Herbert, Quantum Reality: Beyond the New Physics (Anchor, 1987, ISBN 0-385-23569-0)
• D. Wick, The infamous boundary: seven decades of controversy in quantum physics (Birkhauser, Boston 1995)
• R. Anton Wilson, Prometheus Rising (New Falcon Publications, 1997, ISBN 1-56184-056-4)
• Gary Zukav "The Dancing Wu Li Masters" (Perennial Classics, 2001, ISBN 0-06-095968-1)
• Goldstein, Sheldon; et al. (2011). "Bell's theorem". Scholarpedia. 6 (10): 8378. Bibcode:2011SchpJ...6.8378G. doi:10.4249/scholarpedia.8378.

 وصلات خارجية

At Wikiversity, you can learn about: Bell's_theorem

• "On the Einstein Podolsky Rosen Paradox", Bell's original paper.
• Another version of Bell's paper.
• An explanation of Bell's Theorem, based on N. D. Mermin's article, Mermin, N. D. (1981). "Bringing home the atomic world: Quantum mysteries for anybody". American Journal of Physics. 49 (10): 940–943. Bibcode:1981AmJPh..49..940M. doi:10.1119/1.12594.
• Mermin: Spooky Actions At A Distance? Oppenheimer Lecture
• Quantum Entanglement, by Dr Andrew H. Thomas.
• Bell's Theorem with Easy Math, by David R. Schneider. Another simple explanation of Bell's Inequality.
• Bell's theorem on arXiv.org
• Interactive experiments with single photons: entanglement and Bell´s theorem
• Article on Bell's theorem at Stanford encyclopedia of philosophy by Abner Shimony
• Discussion using a recent framework introduced by Gill
• "Bell's theorem". موسوعة الفلسفة على الإنترنت.
• Hazewinkel, Michiel, ed. (2001), "Bell inequalities", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• Spooky Action at a Distance: an Explanation of Bell's Theorem