نسبية التزامن

On spaceships, map-clocks may look unsynchronized.

Event B is simultaneous with A in the green reference frame, but it occurred before in the blue frame, and will occur later in the red frame.

Events A, B, and C occur in different order depending on the motion of the observer. The white line represents a plane of simultaneity being moved from the past to the future.

في الفيزياء، the relativity of simultaneity is the concept that distant simultaneity – whether two spatially separated events occur at the same time – is not absolute, but depends on the observer's reference frame. This possibility was raised by mathematician Henri Poincaré in 1900, and thereafter became a central idea in the special theory of relativity.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الوصف

According to the special theory of relativity introduced by Albert Einstein, it is impossible to say in an absolute sense that two distinct events occur at the same time if those events are separated in space. If one reference frame assigns precisely the same time to two events that are at different points in space, a reference frame that is moving relative to the first will generally assign different times to the two events (the only exception being when motion is exactly perpendicular to the line connecting the locations of both events).

For example, a car crash in London and another in New York appearing to happen at the same time to an observer on Earth, will appear to have occurred at slightly different times to an observer on an airplane flying between London and New York. Furthermore, if the two events cannot be causally connected, depending on the state of motion, the crash in London may appear to occur first in a given frame, and the New York crash may appear to occur first in another. However, if the events can be causally connected, precedence order is preserved in all frames of reference.

 التاريخ

المقالة الرئيسية: تاريخ النسبية الخاصة, History of Lorentz transformations, and Lorentz ether theory

In 1892 and 1895, Hendrik Lorentz used a mathematical method called "local time" t' = t – v x/c² for explaining the negative aether drift experiments. However, Lorentz gave no physical explanation of this effect. This was done by Henri Poincaré who already emphasized in 1898 the conventional nature of simultaneity and who argued that it is convenient to postulate the constancy of the speed of light in all directions. However, this paper did not contain any discussion of Lorentz's theory or the possible difference in defining simultaneity for observers in different states of motion. This was done in 1900, when Poincaré derived local time by assuming that the speed of light is invariant within the aether. Due to the "principle of relative motion", moving observers within the aether also assume that they are at rest and that the speed of light is constant in all directions (only to first order in v/c). Therefore, if they synchronize their clocks by using light signals, they will only consider the transit time for the signals, but not their motion in respect to the aether. So the moving clocks are not synchronous and do not indicate the "true" time. Poincaré calculated that this synchronization error corresponds to Lorentz's local time. In 1904, Poincaré emphasized the connection between the principle of relativity, "local time", and light speed invariance; however, the reasoning in that paper was presented in a qualitative and conjectural manner.

Albert Einstein used a similar method in 1905 to derive the time transformation for all orders in v/c, i.e., the complete Lorentz transformation. Poincaré obtained the full transformation earlier in 1905 but in the papers of that year he did not mention his synchronization procedure. This derivation was completely based on light speed invariance and the relativity principle, so Einstein noted that for the electrodynamics of moving bodies the aether is superfluous. Thus, the separation into "true" and "local" times of Lorentz and Poincaré vanishes – all times are equally valid and therefore the relativity of length and time is a natural consequence.

In 1908, Hermann Minkowski introduced the concept of a world line of a particle in his model of the cosmos called Minkowski space. In Minkowski's view, the naïve notion of velocity is replaced with rapidity, and the ordinary sense of simultaneity becomes dependent on hyperbolic orthogonality of spatial directions to the worldline associated to the rapidity. Then every inertial frame of reference has a rapidity and a simultaneous hyperplane.

In 1990, Robert Goldblatt wrote Orthogonality and Spacetime Geometry, directly addressing the structure Minkowski had put in place for simultaneity. In 2006, Max Jammer, through Project MUSE, published Concepts of Simultaneity: from antiquity to Einstein and beyond. The book culminates in chapter 6, "The transition to the relativistic conception of simultaneity". Jammer indicates that Ernst Mach demythologized the absolute time of Newtonian physics.

Naturally the mathematical notions preceded physical interpretation. For instance, conjugate diameters of a conjugate hyperbolas are related as space and time. The principle of relativity can be expressed as the arbitrariness of which pair are taken to represent space and time in a plane.

 تجارب فكرية

انظر أيضاً: تجارب آينشتاين الفكرية

 قطار آينشتاين

Einstein imagined a stationary observer who witnessed two lightning bolts simultaneously striking both ends of a moving train. He concluded that an observer standing on the train would measure the bolts to strike at different times.

يفضي المبدأ الثاني في النسبية الخاصة الذي يتحدث عن ثبات سرعة الضوء إلى نسبية تزامن حدثين. هذا يعني أن حدثين متزامنين بالنسبة لجملة مقارنة ما سيكونان غير متزامنين بالنسبة لجملة مقارنة أخرى.

ليكن لدينا مسار مستقيم ترتبط به جملة مقارنة S و مقطورة طويلة ترتبط بها جملة مقارنة S' و التي تتحرك على المسار المستقيم بحركة منتظمة سرعتها v . و ليكن في منتصف المقطورة منبع ضوئي Z و في كل من طرفي المقطورة مرآة مستوية A، B .

في لحظة معينة يصدر المنبع الضوئي إشارة ضوئية فيلاحظ المراقب الموجود في جملة المقارنة S' ( المقطورة) أن الإشارة الضوئية تسقط على المرآتين بآن واحد لأن الضوء قطع المسافة نفسها في الحالتين و بسرعة c . و بذلك يكون الحدثان بالنسبة له قد و قعا في مكانين مختلفين و بآن واحد.

أما المراقب الموجود في جملة المقارنة S (المسار) يلاحظ بأن الإشارة الضوئية لا تسقط على المرآتين بآن واحد مع أن سرعة الضوء في جملة مقارنته ينتشر في الاتجاهين بسرعة c مماثلة أيضا لكن المرآة A انتقلت خلال فترة انتشار الإشارة الضوئية من الموضع A إلى الموضع A' ( أقرب للمنبع ) بينما انتقلت المرآة B إلى الموضع B' ( أبعد عن المنبع ) . مما سبق نجد أنه بالنسبة لمراقب موجود على المسار سيصل الضوء إلى المرآة A قبل وصوله إلى المرآة B . بالنسبة لهذا المراقب يقع الحدثان بمكانين مختلفين و بزمنين مختلفين.

لنحلل بشكل أدق ما يشاهده مراقب موجود في جملة المقارنة S المرتبطة بالمسار المستقيم.

ليكن طول المقطورة 2L فيكون الزمن t1 اللازم لوصول الضوء إلى حائط المقصورة الأمامي معطى بالمعادلة :

$c\cdot t_{1}=L+v\cdot t_{1}$

$c\cdot t_{1}$ هي المسافة التي يقطعها الضوء خلال زمن $t_{1}$

$L$ هو بعد الحائط الأمامي عن المنبع في لحظة إصدار الإشارة

$v\cdot t_{1}$ هي المسافة التي يقطعها الحائط الأمامي خلال الزمن الذي تستغرقه الإشارة الضوئية كي تقع على الحائط الأمامي.

من المعادلة السابقة نجد أن

$t_{1}={\frac {L}{c-v}}$

وبنفس الطريقة للزمن اللازم لوقوع الإشارة الضوئية على الحائط الخلفي للمقصورة نحصل على المعادلة التالية:

$c\cdot t_{2}=L-v\cdot t_{2}$

و منه

$t_{2}={\frac {L}{c+v}}$

مما سبق نجد أن t2 < t1 و بالتالي فإن سقوط الإشارة الضوئية على كل من الحائط الأمامي و الخلفي للمقطورة لن يكون في جملة المقارنة S متزامنا.

مما سبق نستنتج أن تزامن حدثين هو أمر نسبي حيث يمكننا التحدث عن تزامن حدثين فقط في حال تم تحديد جملة المقارنة و بذلك يمكن لحدثين في جملتي مقارنة مختلفتين أن يكونا متزامنين فقط إذا وقعا في مكان واحد بالنسبة لجملتي المقارنة.

لنفرض أن هناك راصدين أحدهما في عربة قطار مفتوحة متحركة بسرعة 185000 ميل في الثانية طولها 186000 ميل والأخر في عربة قطار ثابتة أيضا مفتوحة وطولها نفس طول الأخرى وكلا الراصدين يريد أن يقيس سرعة الضوء ولنفرض إن عملية القياس تبدأ عندما تتطابق بداية العربتين ولنفرض أن إشعاعا ليزريا آتيا من اليمين إلى اليسار وبدأت عملية القياس فما هي النتيجة التي سوف يجدها كلا من الراصدين سيجد الراصد الثابت انه عندما دقت ساعة ثانيه واحدة وصل الضوء إلى طرف العربة الأخرى أي انه سرعة 186000 ميل في الثانية وأيضا سوف يجد الراصد المتحرك نفس السرعة ولو كنت تراقب على الرصيف وأنت لا تعرف سوى قوانين نيوتن سوف يبدوا لك أن الراصد المتحرك مخالف للمنطق ولكي نفسر تصرفه هذا سوف نتجه إلى الطرف الأيمن من العربة ونقول انه عندما بعد ثانيه تكون العربة المتحركة متقدمة على الثانية 18500 ميل وانه يتبقى على الإشعاع هذه المسافة كي يقطعها لذلك نرفض تساوي السر عه ولإزالة الشك والغموض عن هذه التجربة نعيدها ولكن على الراصد الثانية مراقبة جميع الأحداث بما فيها الراصد المتحرك وعربته ونطلق الشعاع من جديد وعندما تصل الميقاتيه إلى ثانيه عند الراصد الثابت نحسب القياسات نجد أن الراصد المتحرك لا يكون على بعد 18500 ميل بل على بعد عُشر هذه المسافة وانه لم يسجل ثانيه بل عُشر الثانية فقط وهكذا يتبين أن الراصد الثابت يرى أن المرجع المكاني- الزماني عند الراصد المتحرك ليس هو نفسه المرجع المتحرك عنده ولهذا تتقلص القضبان المتحركة و تبطئ ميقاتيات الحركة النسبية من مرجع لأخر.

Einstein's version of the experiment presumed that one observer was sitting midway inside a speeding traincar and another was standing on a platform as the train moved past. As measured by the standing observer, the train is struck by two bolts of lightning simultaneously, but at different positions along the axis of train movement (back and front of the train car). In the inertial frame of the standing observer, there are three events which are spatially dislocated, but simultaneous: standing observer facing the moving observer (i.e., the center of the train), lightning striking the front of the train car, and lightning striking the back of the car.

Since the events are placed along the axis of train movement, their time coordinates become projected to different time coordinates in the moving train's inertial frame. Events which occurred at space coordinates in the direction of train movement happen earlier than events at coordinates opposite to the direction of train movement. In the moving train's inertial frame, this means that lightning will strike the front of the train car before the two observers align (face each other).

 القطار والرصيف

The train-and-platform experiment from the reference frame of an observer on board the train

Reference frame of an observer standing on the platform (length contraction not depicted)

A popular picture for understanding this idea is provided by a thought experiment similar to those suggested by Daniel Frost Comstock in 1910 and Einstein in 1917. It also consists of one observer midway inside a speeding traincar and another observer standing on a platform as the train moves past.

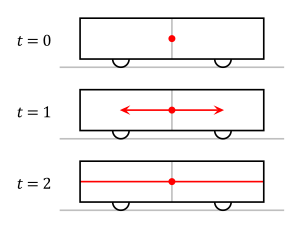
A flash of light is given off at the center of the traincar just as the two observers pass each other. For the observer on board the train, the front and back of the traincar are at fixed distances from the light source and as such, according to this observer, the light will reach the front and back of the traincar at the same time.

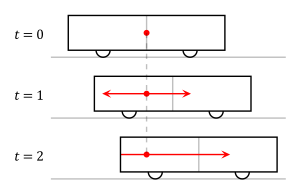
For the observer standing on the platform, on the other hand, the rear of the traincar is moving (catching up) toward the point at which the flash was given off, and the front of the traincar is moving away from it. As the speed of light is finite and the same in all directions for all observers, the light headed for the back of the train will have less distance to cover than the light headed for the front. Thus, the flashes of light will strike the ends of the traincar at different times.

The spacetime diagram in the frame of the observer on the train

The same diagram in the frame of an observer who sees the train moving to the right

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مخططات الزمكان

التزامن و السببية.

في الشكل الأيسر :

لنفترض وجود حدثين أ و ب في نفس الجملة المرجعية و في نفس المكان ضمن هذه الجملة لمن بفاصل زمني ( يشتركان بالموقع المكاني و يختلفان بالاحداثي الزمني ) كما نفترض وجود حدثين ب و ج ضمن جملة مرجعية واحدة بحيث يحدثان آنيا ( أي في وقت واحد ) لكنهما يقعان في موقعين مختلفين . ( يشتركان بالاحداثي الزمني و يختلفان بالاحداثيات المكانية ) .

في الجملة المرجعية الاولى يمكن ل أ أن يسبق ب فعندئذ يكون أ سابقا ل ب في كل الجمل المرجعية و من الممكن للمادة أن تنتقل من أ إلى ب بحيث نعتبر أ سببا و ب نتيجة فتكون هناك علاقة سببية بين أ و ب . في الواقع لا وجود لأي جملة مرجعية تقلب هذا الترتيب السببي .

لكن هذه الحالة لا تنطبق في حالة الحثين أ و ج ( ج يقع خارج المخوط الضوئي ل أ كما هو واضح ) حيث توجد جمل مرجعية ترى حدوث أ قبل ج و جمل مرجعية ترى حدوث ج قبل أ . لكن هذا بكل الأحوال لا يكسر قانون السببية لأنه يستحيل نقل المعلومات بين أو ج أو بين ج و أ لأن هذا يستدعي سرعة أكبر من سرعة الضوء .

It may be helpful to visualize this situation using spacetime diagrams. For a given observer, the t-axis is defined to be a point traced out in time by the origin of the spatial coordinate x, and is drawn vertically. The x-axis is defined as the set of all points in space at the time t = 0, and is drawn horizontally. The statement that the speed of light is the same for all observers is represented by drawing a light ray as a 45° line, regardless of the speed of the source relative to the speed of the observer.

In the first diagram, the two ends of the train are drawn as grey lines. Because the ends of the train are stationary with respect to the observer on the train, these lines are just vertical lines, showing their motion through time but not space. The flash of light is shown as the 45° red lines. The points at which the two light flashes hit the ends of the train are at the same level in the diagram. This means that the events are simultaneous.

In the second diagram, the two ends of the train moving to the right, are shown by parallel lines. The flash of light is given off at a point exactly halfway between the two ends of the train, and again form two 45° lines, expressing the constancy of the speed of light. In this picture, however, the points at which the light flashes hit the ends of the train are not at the same level; they are not simultaneous.

 تحويل لورنتس

The relativity of simultaneity can be demonstrated using the Lorentz transformation, which relates the coordinates used by one observer to coordinates used by another in uniform relative motion with respect to the first.

Assume that the first observer uses coordinates labeled t, x, y, and z, while the second observer uses coordinates labeled t′, x′, y′, and z′. Now suppose that the first observer sees the second observer moving in the x-direction at a velocity v. And suppose that the observers' coordinate axes are parallel and that they have the same origin. Then the Lorentz transformation expresses how the coordinates are related:

$$t'={\frac {t-{v\,x/c^{2}}}{\sqrt {1-v^{2}/c^{2}}}}\,,$$

$$x'={\frac {x-v\,t}{\sqrt {1-v^{2}/c^{2}}}}\,,$$

$$y'=y\,,$$

$$z'=z\,,$$

where c is the speed of light. If two events happen at the same time in the frame of the first observer, they will have identical values of the t-coordinate. However, if they have different values of the x-coordinate (different positions in the x-direction), they will have different values of the t' coordinate, so they will happen at different times in that frame. The term that accounts for the failure of absolute simultaneity is the vx/c².

A spacetime diagram showing the set of points regarded as simultaneous by a stationary observer (horizontal dotted line) and the set of points regarded as simultaneous by an observer moving at v = 0.25c (dashed line)

The equation t′ = constant defines a "line of simultaneity" in the (x′, t′) coordinate system for the second (moving) observer, just as the equation t = constant defines the "line of simultaneity" for the first (stationary) observer in the (x, t) coordinate system. From the above equations for the Lorentz transform it can be seen that t' is constant if and only if t − vx/c² = constant. Thus the set of points that make t constant are different from the set of points that makes t' constant. That is, the set of events which are regarded as simultaneous depends on the frame of reference used to make the comparison.

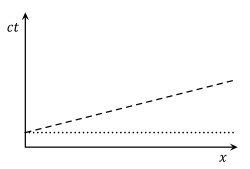
Graphically, this can be represented on a spacetime diagram by the fact that a plot of the set of points regarded as simultaneous generates a line which depends on the observer. In the spacetime diagram, the dashed line represents a set of points considered to be simultaneous with the origin by an observer moving with a velocity v of one-quarter of the speed of light. The dotted horizontal line represents the set of points regarded as simultaneous with the origin by a stationary observer. This diagram is drawn using the (x, t) coordinates of the stationary observer, and is scaled so that the speed of light is one, i.e., so that a ray of light would be represented by a line with a 45° angle from the x axis. From our previous analysis, given that v = 0.25 and c = 1, the equation of the dashed line of simultaneity is t − 0.25x = 0 and with v = 0, the equation of the dotted line of simultaneity is t = 0.

In general the second observer traces out a worldline in the spacetime of the first observer described by t = x/v, and the set of simultaneous events for the second observer (at the origin) is described by the line t = vx. Note the multiplicative inverse relation of the slopes of the worldline and simultaneous events, in accord with the principle of hyperbolic orthogonality.

 الملاحظون المتسارعون

Roundtrip radar-time isocontours

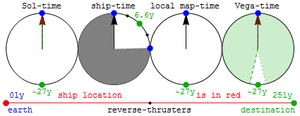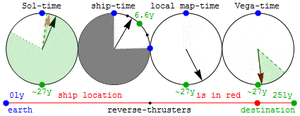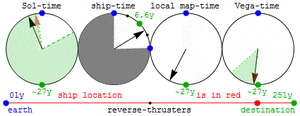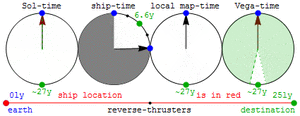
The Lorentz-transform calculation above uses a definition of extended-simultaneity (i.e. of when and where events occur at which you were not present) that might be referred to as the co-moving or "tangent free-float-frame" definition. This definition is naturally extrapolated to events in gravitationally-curved spacetimes, and to accelerated observers, through use of a radar-time/distance definition that (unlike the tangent free-float-frame definition for accelerated frames) assigns a unique time and position to any event.

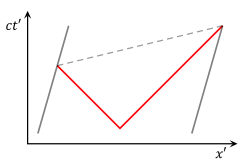
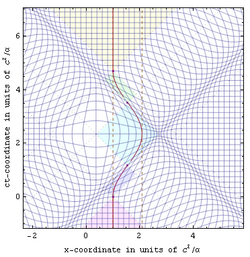
The radar-time definition of extended-simultaneity further facilitates visualization of the way that acceleration curves spacetime for travelers in the absence of any gravitating objects. This is illustrated in the figure at right, which shows radar time/position isocontours for events in flat spacetime as experienced by a traveler (red trajectory) taking a constant proper-acceleration roundtrip. One caveat of this approach is that the time and place of remote events are not fully defined until light from such an event is able to reach our traveler.

 انظر أيضاً

• مفارقة أندروميدا
• Causal structure
• تجارب آينشتاين الفكرية
• مفارقة إرنفست
• Einstein synchronisation

 وصلات خارجية

• Special relativity at Wikibooks