معيار تشفير المعطيات

Data Encryption Standard
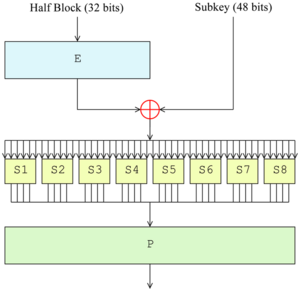
Data Encryption Standard InfoBox Diagram.png
The Feistel function (F function) of DES
عام
المصممونIBM
أول نشر1977 (standardized on January 1979)
مشتق منLucifer
اللاحقونTriple DES, G-DES, DES-X, LOKI89, ICE
تفاصيل الشفرة
حجم المفاتيح56 bits
أحجام الكتل64 bits
البنيةBalanced Feistel network
الدورات16
أفضل تحليل تعموي عمومي
DES is now considered insecure because a brute force attack is possible (see EFF DES cracker). As of 2008, the best analytical attack is linear cryptanalysis, which requires 243 known plaintexts and has a time complexity of 239–43 (Junod, 2001); under a chosen-plaintext assumption, the data complexity can be reduced by a factor of four (Knudsen and Mathiassen, 2000).

معيار تشفير المعطيات Data Encryption Standard-DES هو التشفير المتناظر الأكثر استخداماً. ومع أنه تم الاتفاق على استبدال هذه الخوارزمية بخوارزمية "مقياس التشفير المتقدم " (Advanced Encryption Sartndard-AES) بقيت خوارزمية DES الأكثر أهمية بين الخوارزميات المتشابهة. بالاضافة إلى ما تم ذكرة تعتبر دراسة خوارزمية DES بشكل مفصل الأساس لفهم المبادئ المستخدمة في الشتفير المتناظر. سنقوم في الفصول 5 و6 بدراسة مجموعة طرق التشفير المتناظر الهامة بما في ذلك AES.

تعتبر خوارزمية DES ومعظم خوارزميات التشفير المتناظر معقدة جدا، اذا ما قورنت بخوارزميات المفتاح العمومي مثل RSA، وبالتالي لا يمكن شرحها ببساطة كما هي الحال في خواركية RSA والخوارزميات المتشابهة. لذلك سنبدأ بنسخة مبسطة للخوارزمية DES. تسمح هذه النسخة للقارئ باجراء عمليتي التعمية وفك التعمية يدويات وذلك من أجل اكتساب الفهم الجيد لكيفية عمل هذه الخوارزمية. وقد دلت خبرات التدريس على أن الفهم الجيد لهذه النسخة المبسطة يحسن ويسهل فهم خوارزمية DES.

يبحث هذا الكتاب، بعد مناقشة النسخة المبسطة من DES، في المبادئ العامة للتشفير الكتلي المتناظر ، والذي يمثل نوع التشفير المتناظر الذي سيتم بحثه في هذا الكتاب (ماعدا التشفير التسلسلي RCS المطروح في الفصل السادس). ثم ينتقل الكتاب بعد ذلك إلى عرض خوارزمية DES الكاملة. يعود الكتاب، بعد مناقشة هذه الخوارزمية الخاصة، إلى مناقشة عامة لتصميم أنظمة التشفير الكلي.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

خوارزمية DES المبسطة

تعتبر خوارزمية DES المبسطة (S- DES) والتي تم تطويرها من قبل البروفيسور إدوارد شيفر في جامعة سانتا كلارا، خوارزمية تعليمية أكثر من كونها خوارزمية آمنة للعمل الحقيقي، تمتلك هذه الخوارزمية نفس خصائص وبنية خوارزمية DES ولكن مع معاملات أصغر بكثير يمكن للقارئ أن يجدها مريحة في العمل اليدوي لتطبيق الأمثلة الواردة أثناء مناقشة هذا المقطع.


نظرة عامة

يوضح الشكل 3-1 البنية العامة للخوارزمية S- DES . دخل خوارزمية التعمية S- DES، هو كتلة ذات ثماني خانات من النص الصريح (على سبيل المثال 10111101)، بالإضافة إلى مفتاح بطول عشر خانات. أما خرجها فهو عبارة عن كتلة من النص المشفر بطول ثماني خانات أيضا. أما خوارزمية S- DES لفك التعمية فهي تأخذ كتلة من النص المشفر بطول ثماني خانات بالاضافة إلى نفس المفتاح ذي العشر خانات لتعطي كتلة ذات طول ثماني خانات من النص الصريح.

تتضمن خوارزمية التعمية خمسة توابع: التبديل الأولي للمواقع (IP)؛ وظيفة معقدة باسم Fk، والتي تتضمن عمليتي تبديل أحرف وتبديل مواضع معتمدتين على المفتاح، عملية تبديل مواقع بسيطة (SW)، تقوم بتبديل مواقع نصفي المعطيات بين بعضها بعض، ثم الوظيفة Fk مرة أخرى، وأخيرا وظيفة تبديل المواقع التي تعاكس عملية التبديل الأولى للمواقع والتي يشار إليها بالرمز (IP-1). تؤدي المراحل المتعددة في عمليات تبديل الحروف وتبديل المواقع، كما أشرنا في الفصل الثاني، إلى انتاج خوارزميات معقدة، تزيد الصعوبات أمام محللي التشفير.

دخل التابع Fk، هو كتلة خانات المعطيات المراد تشفيرها (بعد مرورها بالتابع IP) بالاضافة إلى ثماني خانات من المفتاح. كان من الممكن تصميم الخوارزمية لتعمل مع مفتاح بطول ستة عشرة خانة، بحيث يتم تقسيمه إلى مفتاحين جزئيين طول كل منهما ثماني خانات. وبحيث يتم استخدام كل جزء مع إحدى الوظائف Fk المكررة في الخوارزمية. يمكن عوضا عن ذلك استخدام مفتاح وحيد بطول 8 خانات بحيث يستخدم نفسه مرتين في الخوارزمية. الحل الأمثل هو استخدام مفتاح بطول 10 خانات، بحيث يتم توليد مفتاحين منه طول كل منهما 8 خانات وذلك كما هو موضح في الشكل 3-1. وفي هذه الحالة يطبق على المفتاح تابع تبديل المواضع P10 والذي سينتج خرجا ذو ثماني خانات هو المفتاح الأول K1. كذلك يطبق خرج عملية الازاحة على عملية ازاحة أخرى ومن ثم على عملية تبديل المواقع P8، لانتاج المفتاح الثاني K2 ذو الثماني خانات.

{{{{الشكل 3-1: مخطط خوارزمية DES المبسطة}}}}

يمكن التعبير عن خوارزمية التعمية باختصار كتركيب للتوابع كما يلي:

IP-1 o fk2oSWk1oIP والذي يمكن كتابته أيضا كما يلي:

Ciphertext = IP-1 (fk2 (SW(fk1(IP(plaintext))))

حيث: K1=P8 (shift(P10(Key))) K2= P8(Shift(shift(P10(key))))

يبين الشكل 3-1 أيضا عملية فك التعمية والذي يعتبر بشكل مبدئي عكس عملية التشفير:

Plaintext – (IP-1(fk1(SW(fk2(IP(ciphertext))))

سنقوم الآن بدراسة عناصر خوارزمية S-DES بالتفصيل.


توليد مفاتيح الخوارزمية S-DES

تعتمد خوارزمية S-DES على استخدام مفتاح مشترك بين المرسل والمستقبل بطول عشرة خانات. يتم انتاج مفتاحين جزئيين من هذا المفتاح، طول كل واحد ثماني خانات وذلك لاستخدامهما في المراحل المختلفة من خوارزمية التشفير وفك التشفير. يوضح الشكل 3-2 الخطوات المتبعة لانتاج المفاتيح الجزئية.

تقوم الخطوة الأولى بعملية تبديل مواقع خانات المفتاح بالطريقة التالي. لنعطي خانات المفتاح العشر رموزا كما يلي P10(K1,K2,K3,K4,K4,K5,K6,K7,K8,K9,K10)

يمكن التعبير عن التابع P10 باختصار في الشكل التالي:

P10 9 8 9 1 10 4 7 2 2 5 3

يقرأ هذا الجدول من اليسار إلى اليمين، حيث يعبر محتوى كل موضع في الجدول عن هوية خانة الدخل التي ستعطي خانة الخرج في هذا الموضع. وبالتالي خانة الخرج الأولى ستكون هي خانة الدخل الثالثة، وخانة الخرج الثانية ستكون هي خانة الدخل الخامسة.. وهكذا. فعلى سبيل الثمال اذا كان مفتاح الدخل هو (1010000010) فان خرج تابع تبديل المواضع P10 سيكون الخمس خانات الأولى والخمس خانات الثانية من خرج عملية تبديل المواقع P10 بشكل مستقل وبالتالي فإن خرج هذه العملية سيكون (000001 11000).

نقوم بعد ذلك بتطبيق تابع تبديل المواضع P8 والذي يقوم بانتخاب وتبديل مواقع ثماني خانات من أصل عشرة وذلك حسب القاعدة التالية:

P8 9 10 5 8 4 7 3 6

وستكون النتيجة هي المفتاح الجزئي الأول k1 وفي مثالنا سوف ينتج (10100100).

نعود بعد ذلك إلى زوج السلاسل المؤلفة من خمس خانات الناتجة عن عمليتي الازاحة SL-1 ونطبق عليهما عمليتي ازاحة دوارنيتين بمقادر خانتين لكل منهما، وهو ما يعبر عنه بالتوابع SL-2 في الشكل 3-2. ستكون النتيجة في مثالنا هي (0010000011). نقوم أخيرا بتطبيق تابع تبديل المواقع P8 نفسه على الناتج للحصول على المفتاح الجزئي الثاني K2، والذي سيكون في مثالنا (001000011).

{{{الشكل 3-2:توليد المفاتيح في خوارزمية DES المبسطة}}}

التعمية حسب خوارزمية S-DES

يبين الشكل 3-2 خوارزمية التعمية S-DES بالتفصيل. تتألف عملية التعمية، كما ذكرنا سابقا، من تطبيق متسلسل لخمسة توابع. سندرس كل من هذه التوابع بشكل مستقل.

{{{الشكل 3-3: مخطط تفصيلي للتعمية وفق خوارزمية S-DES}}}

تبديلات المواقع البدائية والنهائية

يتألف دخل الخوارزمية من كتلة من معطيات الدخل بطول ثماني خانات، والتي يطبق عليها تابع تبديل المواقع IP التالي:

IP 7 5 8 4 1 3 6 2


من الواضح أن خرج هذا التابع هو نفس خانات الدخل ولكن بعد تبديل مواقعها، ولذلك نرى أنه سيتم تطبيق التابع IP-1 لعكس هذا الترتيب في نهاية الخوارزمية.

IP-1 6 8 2 7 5 3 1 4

يمكن ببساطة عن طريق مثال توضيح أن عملية تبديل المواقع التالية هي في الحقيقة عكس عملية الترتيب الأولى تماما، أي أن IP-1 (IP (x))=x

التابع fk

يعتبر التابع fk العنصر الأكثر تعقيدا بينا عناصر الخوارزمية S-DES ، حيث يتألف من مجموعة توابع تبديل المواقع وتبديل الحروف. يمكن وصف هذا التابع كما يلي: لنفرض أن L وR هي عبارة عن الخانات الأربع اليسارية والخانات الأربع اليمينية من الدخل المؤلف من ثماني خانات للتابع fk على الترتيب، ولنفرض أن F هي عبارة عن عملية تحويل من سلسلة ذات أربع خانات إلى سلسلة أخرى ذات أربع خانات أيضا (ليس بالضرورة أن يكون التحويل واحدا واحدا). عندها يمكن أن نكتب :

Fk (L,R) = (L ө F(R, SK),R

حيث أن SK هو عبارة عن المفتاح الجزئي، و өهي عبارة عن عملية PR القسرية Exclusive-OR) المطبقة على مستوى الخانة. لنفرض على سبيل المثال أن خرج المرحلة IP في الشكل 3-3 هو (10111101) وأن F(1101, SK) = (1110) من أجل SK ما، عندها سيكون fK (10111101) = (0101 1101) وذلك لأن (1011) ө (1110) = (0101).

سنقوم الآن بشرح عملية التحويل F. دخل هذه العملية هو عبارة عن رقم من أربع خانات (n1 n2 n3 n4). الخطوة الأولى في هذا التحويل هي عبارة عن عملية توسيع وتبديل مواقع كما هو مبين فيما يلي:

E/P 1 4 3 2 3 2 1 4

من الأفضل كتابة هذه الخطوة كما يلي وذلك للاستفادة منه لاحقا:

n3 n2 n1 n4 n1 n4 n3 n2

تتم بعد ذلك اضافة المفتاح الجزئي ذو الثماني خانات k1= (k11,k12,k13,k14,k15,k16,k17,k18) إلى القيمة السابقة باستخدام XOR: n3+ k14 n2+ k13 n1+ k12 n4+ k11 n1+k18 n4+k17 n3+ k16 n2+ k15

لنقم الآن باعادة تسمية هذه الخانات الثمانية:

P0.3 P0.2 P0.1 P0.0 P1.3 P1.2 n3 P1.0

يتم ادخال الأربع خانات الأولى (السطر الأول في المصفوفة السابقة) إلى صندوق S المسمى SO لانتاج خانتي خرج، كذلك يتم إدخال الأربع خانات الباقية (السطر الثاني) إلى الصندوق S1 لإنتاج خانتي خرج أيضا. تعرف هذه الصناديق كما يلي:

{{{شكل الصناديق}}}

تعمل صناديق S كما يلي: تعامل خانتا الدخل الأولى والرابعة كعدد واحد مؤلف من خانتين لتحديد رقم السطر في الصندوق S، بينما تحدد الخانتان الثانية والثالثة رقم العمود في نفس الصندوق. يعتبر الرقم الواقع في تقاطع السطر والعمود المحددان خرج الصندوق بعد تمثيله ثنائيا وبخانتين فقط. فعلى سبيل المثال اذا كان (P0.0 P0.3) = (00) وكان (P0.1 P0.2) = (10) عندها سيتم الحصول على الخرج من السطر رقم 0 والعمود رقم 2 من الصندوق S0، أي سيكون الخرج هو 3 أو 2(11) . تستخدم الخانات (P11 P12) = (P10 P13) لتحديد السطر والعمود في صندوق S1 وبالتالي الحصول على خانتي خرج إضافيتين.

يتم بعد ذلك تطبيق عملية تبديل مواقع على الخانات الأربع الناتجة من الصناديق S0 وS1 كما يلي:

P4 1 3 4 2


تابع التبديل

قام التابع fk بتبديل الخانات الأربع اليسارية فقط. لذلك يقوم تابع التبديل (SW) بتبديل الأربع خانات اليسارية مع الأربع خانات اليمينية وذلك كي يعالج التابع fk، والذي سيتم تطبيقه مرة أخرى على الخانات الأربع التالية. في المرحلة الثانية يتم تكرار تطبيق التوابع P4, S1, S0, E/P ذاتها ، غير أن المفتاح في هذه المرحلة سيكون k2.

تحليل خوارزمية DES المبسطة

يعتبر كسر خوارزمية DES المبسطة بالتجريب محققا حتما. فعندما يكون طول المفتاح عشر خانات فإنه يوجد 210 = 1024 احتمالا فقط. فاذا كان لدينا نص مشفر ما، عندها يمكن تجريب كل حالة من حالات المفتاح وتحليل النتيجة لمعرفة فيما اذا كان النص الناتج مقروءا أم لا.

ماذا عن تحليل التعمية؟ لنفرض حالة الهجوم على نص صريح معروف، حيث لدينا نص صريح واحد معروف هو (P1,P2, P3. P4, P5, P6, P7, P8) والنص المشفر المرافق له معروف أيضا وهو (c1,c2,c3,c4,c5,c6,c7,c8)أما المفتاح (k1,k2,k3,k4,k5,k6,k7,k8,k9k,k10) فهو غير معروف. يمكن في هذه الحالة وصف كل c1 على شكل تابع كثير حدود g1 للمعاملات k1, p1. يمكن بهذا الشكل التعبير عن عملية التعمية بثماني معادلات غير خطية ذات عشرة مجاهيل. هناك عدد من الحلول المحتملة، ولكن يجب حساب كل منها وتحليله. إن عمليتي تبديل المواقع والاضافة هما عمليتان خطيتان في الخوارزمية. وتأتي عدم الخطية من الصناديق s. لذلك من المفيد كتابة المعادلات التي تصف هذه الصناديق. وللتوضيح فقط سنقوم بتغير تسمية المتحولات لتصبح كما يلي: (P0.0, P0.1, P0.2, P0.3) = (a, b, c, d) و (P1.0, P1.1, P1.2, P1.3) = (w, x,y, z) وسنسمي الخرج ذا الأربع خانات (q, r, s, t). عندها يمكن وصف العملية S0 بالمعادلات التالية:

Q = abcd + ab +ac + b +d R = abcd +abd + ab + ac + a + c +1

حيث تتم كل عمليات الجمع بالقياس 2. يمكن بنفس الطريقة كتابة المعادلات التي تصف S1. استبدال هذه المعادلات غير الخطية بتحويلات خطية سينتج تعابير كثيرات حدود معقدة جدا، مما يجعل عملية تحليل التعمية صعبة جدا. ولتوضيح المشكلة يجب ملاحظة أن للمعادلات كثيرة الحدود بعشرة مجاهيل في الحسابات الثنائية 210 حدا محتملا. وبشكل وسطي يمكن أن نتوقع لكل معادلة من المعادلات الثماني حوالي 29 حدا. يمكن للقارئ المهتم أن يجرب وضع هذه المعادلات باستخدام أي معالج رموز ومن المؤكد أن القارئ أو البرنامج سيتسلم قبل المضي طويلا في المعالجة.

الارتباط بخوارزمية DES

تتعامل خوارزمية DES مع كتلة دخل بطول 64 خانة، يمكن التعبير عن مخطط التعمية كما يلي: IP -1 ofk16 ofk15 oSW …….oSW ofx1oIP

يستخدم مع هذه الخوارزمية مفتاح بطول 56 خانة، حيث يتم توليد 16 مفتاحا فرعيا منه طول كل منها 48 خانة. هناك عملية تبديل مواقع أولية ل56 خانة، تتبع بسلسلة من عمليات الازاحة وتبديل المواقع ل48 خانة.

يتم الاستعاضة ضمن خوارزمية التعمية عن التابع F الذي يؤثر على أربعة خانات (n1, n2,n3,n4) بآخر يتعامل مع 32 خانة (n1,n2,n3 …n32). يمكن بعد عملية توسيع/تبديل المواقع الأولية التعبير عن الخرج ذي الثماني والأربعين خانة بالشكل:

{{{شكل توضيحي}}}}

تتم اضافة هذه المصفوفة بواسطة (XOR) إلى المفتاح الفرعي ذو الثماني والأربعين خانة. هناك ثمانية أسطر موافقة لثمانية صناديق S. لكل صندوق S أربعة أسطر وستة عشر عمودا. الخانتان الأولى والأخيرة من أسطر المصفوفة السابقة تحددان رقم السطر في الصندوق S، بينما تحدد الخانات الأربع في الوسط رقم العمود في هذا الصندوق.


مبادئ التشفير الكتلي

تعتمد كل خوارزميات التشفير الكتلي المتناظر المستخدمة حاليا على البنية المسماة تشفير فسيتيل الكتلي (Feistel Black Cipher) . لذلك من الضروري دراسة مبادئ تشفير فيستيل. سنبدأ هذه الدراسة بمقارنة بين التشفير الكتلي والتشفير التسلسلي. سندرس بعد ذلك الدوافع وراء تشفير فيستيل، ومن ثم ننتقل إلى بعض ما يتضمنه هذا التشفير.


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

التشفير التسلسلي والتشفير الكتلي

التشفير السيلي هو ذاك النوع من التشفير الذي يقوم بتعمية سيالة من المعطيات الرقمية بشكل تسلسلي، بحيث تتم تعمية خانة واحدة أو ثمانية واحدة (byte) في كل لحظة زمنية. من أهم الأمثلة الكلاسيكية على التشفير التلسلي يمكن أن نذكر تشفير فيجينر وتشفير فيرنام. أما في التشفير الكلي فتتم معالجة كتلة من النص الصريح كوحدة متكاملة بحيث تنتج كتلة من النص المشفر مساوية لها في الطول. طول الكتلة القياسية المستخدمة هو 64 خانة أو 128 خانة. يمكن باستخدام بعض أنماط العمل الخاصة، التي سيتم توضيحها لاحقا، جعل التشفير الكتلي يعطي نفس تأثير التشفير التسلسلي.

لقد انصبت الجهود بشكل أساسي على تطوير التشفير الكتلي، ويعود السبب في ذلك إلى المجال الأكبر للتطبيقات التي يمكن أن تستخدم هذا النوع من التشفير. معظم تطبيقات التعمية المتناظرة الخاصة بالشبكات تستخدم التشفير الكتلي. نتيجة لما سبق سنركز في هذا الفصل على التشفير الكتلي وفي فوصل الكتاب الآتية الخاصة بالتعمية المتناظرة.

الدوافع لبنية تشفير فيستيل

يعمل التشفير الكتلي على كتلة نص صريح بطول n خانة وذلك لانتاج كتلة نص مشفر بطول n خانة. هناك 2n احتمالا مختلفا من كتل النص الصريح، وحتى تكون عملية التعمية عكوسة (أي حتى يكون من الممكن إجراء فك التعمية) ، يجب أن ينتج كل احتمال من هذه الاحتمالات نصا مشفرا فريدا. يدعى هذا النوع من التحويل بالعكوس. توضح الأمثلة التالية التحويلات العكوسة وغير العكوسة من أجل n = 2.

تحويل معكوس النص الصريح النص المشفر 00 11 01 10 10 00 11 01


تحويل غير معكوس النص الصريح النص المشفر 00 11 01 10 10 01 11 01

نلاحظ في الحالة الأخيرة أنه يمكن إنتاج الشفرة 01 من إحدى كتلتي نص صريح متباينتين، لذلك لا يمكن اعتبار هذا النوع من التحويل عكوس، أي إذا كان لدينا النص المشفر 01 فلا يمكن معرفة النص الصريح المرتبط به بدقة.

يوضح الشكل 3-4 منطق التشفير بتبديل الحروف عموما، ولذلك من أجل n=4. يمكن للدخل المؤلف من أربع خانات أن يأخذ ست عشرة حالة دخل ممكنة، والتي يمكن ربطها عن طريق التشفير بتبديل الحروف بست عشرة حالة خرج فريدة، بحيث يمكن تمثيل كل منها بأربع خانات من النص المشفر. يمكن وصف تحويلات التعمية وفك التعمية بالجداول كما هو مبين في الجدول 3-1. تعتبر هذه الحالة الشكل الأكثر عمومية للتشفير الكتلي والذي يمكن استخدامه لتعريف أي عملية تحويل عكوسة بين النص الصريح والنص المعمى.

هناك مشكلة عملية مرتبطة بهذه الطريقة. إذا تم استخدام كتلة صغيرة نسبيا، مثل n=4 عندها سيكافئ هذا النظام التشفير التقليدي بتبديل الحروف والذي يعتبر ضعيفا تجاه التحليل الاحصائي. لا تنتج نقطة الضعف هذه نتيجة استخدام التشفير "تبديل الحروف" ، إنما تنتج من استخدام كتلة صغيرة الحجم نسبيا. أما اذا كان "كبير بشكل كاف وكان بالامكان تغيير قاعدة التحويل بين النص الصريح والنص المشفر، عندها ستضيع الخصائص الاحصائية للنص الصريح وسيصبح كسر التعمية بهذه الطريقة غير فعال.

{{{{الشكل 3-4: عملية تبديل حروف عامة n خانة n- (n-4)

يعتبر التشفير بتبديل الحروف، عندما يكون حجم الكتلة كبيرا وعندما يمكن تغيير قاعدة التحويل بشكل حر غير عملي من وجخة نظر التطبيق والآداء معا. حيث تعتبر عملية التحويل في هذه الحالة هي بحد ذاتها مفتاح التعمية. لننظر مرة أخرى إلى الجدول 3-1 والذي يعرف عملية تحويل عكوسة من النص الصريح إلى النص المشفر وذلك من أجل n=4. يتم تعريف التحويل عن طريق مداخل أو خلايا العمود الثاني والتي تبين قيم النص المشفر المرافقة لكل كتلة ممكنة من النص الصريح وهذا في الجوهر هو المفتاح الذي يحدد عملية تحويل ما من بين جميع عمليات التحويل الممكنة. يتطلب المفتاح في هذه الحالة 64 خانة. وبشكل عام من أجل التشفير الكتلي بتبديل الحروف وبطول n خانة، يكون طول المفتاح هو n X 2n. فمن أجل كتلة بطول 64 خانة (وهي الحالة المطلوبة لمقاومة الكسر بطريقة الاحصاء) سيكون طول المفتاح هو 64 X 264 = 270 = 1021.

الجدول 3-1 جداول التعمية وفك التعمية من أجل التشفير بتبديل الحروف الواردة في الشكل 3-4

{{{{{جدول 3-1}}}}}

أخذ فيستيل هذه الصعوبات بعين الاعتبار، وأشار إلى أن المطلوب هو الاقتراب من نظام التشفير الكتلي المثالي ذو عدد الخانات n الكبير نسبيا، والذي يجب بناؤه من مجموعة من العناصر سهلة التحقيق. ولكن قبل الانتقال إلى طريقة فيستيل لابد من وضع ملاحظة أخرى. يمكننا تقييد أنفسنا بهذا التشفير العام بتبديل الحروف لكن، لجعل عملية التطبيق ممكنة، سنقيد أنفسنا بمجموعة جزئية من احتمالات التحويل العكوسة والتي عددها 2n، لنفرض على سبيل المثال، أننا حددنا التحويل على شكل مجموعة من المعادلات الخطية. فعندما يكون n=4 سيكون لدينا:

Y1 = k11 x1 + k12 x2 + k 13 x3 + k14 x4 Y2 = k21 x1 + k22 x2 + k23 x3 + k24 x4 Y3 = k31 x1 + k32 x2 + k33 x3 + k34 x4 Y4= k412 x1 + k42 x2 + k43 x3 + k44 x4

حيث أن x1 هي الخانات الأربع لكتلة النص الصريح، وy1 هي الخانات الأربع لكتلة النص المشفر، أما kij فهي عبارة عن معاملات ثنائية، علما بأن جميع العمليات الحسابية تجرى بالقياس 2. طول المفتاح هو n2 فقط، وفي هذه الحالة سيكون 16 خانة.

تنبع خطورة هذا النوع من التشكيل من الضعف تجاه تحليل التعمية من قبل مهاجم لدية معلومات عن بنية الخوارزمية. ما لدينا في هذا المثال هو في الحقيقة تشفير هيل الذي تمت مناقشته في الفصل الثاني، ولكن مطبق على معلومات ثنائية بدلا من الحروف. وكما رأينا في الفصل الثاني هذا النظام الخطي ضعيف جدا تجاه الكسر.

تشفير فيستيل

اقترح فيستيل أنه يمكن تطوير تشفير تبديل الحروف البسيط عن طريق تطبيق مفهوم ضرب التشفير، حيث يمكن تطبيق تشفيرين متتالين أو أكثر بحيث تكون النتيجة النهائية، من وجهة نظر التعمية، أقوى من أي من مركباتها. وفي الحقيقة ما لدينا هو عبارة عن تطبيق عملي لمقترح كلاود شانون (claude Shannon) بانتاج تشفير مؤلف من تعاقب تابعي البعثرة والنشر (Confusion and Dissusion).

سنلقي نظرة على هذين المفهومين ومن ثم نتابع شرح تشفير فيستيل. لكن أولا من الجدير التعليق على الحقيقة التالية: معظم بنى أنظمة التشفير الكتلي المتناظر الهامة والمستخدمة في هذه الأيام مبنية على أساس بنية نظام تشفير فيستيل، الذي يعود لحوالي ربع قرن ماضي والمبني على أساس اقتراح شينون عام 1945.

النشر والبعثرة

تم طرح تعبيري النشر والبعثرة من قبل كلاود شانون للاحاطة بحجري الأساس في أي نظام تعمية. انصبت اهتمامات شانون على مقاومة تحليل التعمية المعتمد على التحليل الاحصائي وقد انبثقت حجته في ذلك مما يلي: لنفرض أنه لدى المهاجم معلومات ما عن الخصائص الاحصائية للنص الصريح. فعلى سبيل المقال يمكن معرفة توزع تردد ظهور الأحرف في رسالة ما اذا ما عرفت لغة هذه الرسالة. أو يمكن أن تكون هناك عبارة أو كلمات ستظهر حتما في الرسالة. اذا ظهرت هذه الاحصائيات بأي شكل من الأشكال في النص المشفر، عندها سيتمكن المحلل من تخمين مفتاح التعمية، أو جزءا منه، أو على الأقل ممكن أن يخمن مجموعة من المفاتيح التي تحوي على المفتاح المطلوب. أشار شانون إلى أنه في نظام التشفير القوي المثالي يجب أن تكون كل المعلومات الاحصائية للنص المشفر مستقلة عن المفتاح الخاص المستخدم. ويعتبر نظام التشفير بتبديل الحروف مع امكانية تبديل قواعد التحويل بشكل حر هو النظام المطلوب، إلا أنه للاسف غير عملي، كما رأينا.

بالاضافة إلى الاستعانة بالنظام المثالي، اقترح شانون طريقتين لاحباط تحليل التعمية الاحصائي: النشر والبعثرة. في النشر يتم تشتيت البنية الاحصائية للنص الصريح في مجال طويل من احصائيات النص المشفر، يمكن انجاز ذلك عن طريق تاثير كل رقم من النص الصريح على قيم عدة أرقام من النص المشفر، أو ما يكافئ القول بأن كل من النص المشفر يتم التاثير عليه من قبل عدة أرقام من النص الصريح. والمثال على عملية النشر هو تشفير رسالة ما من المحارف M= m1, m2, m3 … عن طريق عملية المعدل الوسطي كما يلي:

{{{{معادلة يجب أن تصور}}}}}

أي باضافة k حرف متتالي للحصول على حرف مشفر واحد yn. يمكن تبيان كيف تمت ازالة البنية الاحصائية للنص الصريح. أي أن تردداد ظهور الحروف في النص المشفر ستكون متقاربة. كذلك الأمر بالنسبة لتردد ظهور الثنائيات .. وهكذا. يمكن في التشفير الكتلي الثنائي انجاز عملية النشر عن طريق القيام بعملية تبديل مواقع متكررة للمعطيات ومن ثم تطبيق تابع ما على هذا التبديل. وفي النهاية سيكون التاثير الحاصل هو تأثير خانات من مواقع مختلفة من النص الصريح على خانة واحدة من النص المشفر.

تتضمن عملية التشفير الكتلي تحويل كتلة من النص الصريح إلى كتلة من النص المشفر، حيث تعتمد عملية التحويل على المفتاح. تسعى آلية النشر إلى أن تكون العلاقة الاحصائية بين النص الصريح والنص المشفر أعقد ما يكون. وذلك لمقاومة محاولات تخمين المفتاح. تسعى عملية البعثرة من الطرف الآخر إلى جعل العلاقة بين احصائيات النص المشفر وقيمة مفتاح التشفير أعقد ما يكون، وذلك من أجل مقاومة محاولات اكتشاف المفتاح أيضا.

وبالتالي، حتى لو استطاع المهاجم تجميع معلومات احصائية معينة حول النص المشفر، فإنه لن يستطيع تخمين المفتاح المستخدم بسبب تعقيد طريقة استخدام المفتاح لانتاج النص المشفر. يتم انجاز ذلك عن طريق خوارزمية تبديل حروف معقدة.

تعتبر عملية النشر والبعثرة الناجحة جوهر عملية التشفير الكتلي والتي أصبحت حجر الأساس في تصميم نظم التشفير الكتلي الحديثة.

بنية نظام تشفير فيستيل

يبين الشكل 3-5 البنية المقترحة من قبل فيستيل. دخل خوارزمية التشفير هو عبارة عن كتلة من النص الصريح بطول 2w والمفتاح k. يتم تقسيم كتلة النص الصريح إلى نصفين L0 وR0. يمر هذا النصفان من خلال n حلقة معالجة ومن ثم يتم ضمهمها لانتاج كتلة النص المشفر. دخل الحلقة i هو Li-1 وRi-1 الناتجين من الحلقة السابقة بالاضافة إلى المفتاح الجزئي k1 الناتج من المفتاح الأساسي k. المفاتيح الجزئية ki مختلفة بشكل عام عن المفتاح الاساسي k وعن بعضها البعض.

{{{{الشكل 3-5: شبكة فيستيل التقليدية}}}}

تملك كل الحلقات نفس البنية تماما. يتم تطبيق عملية تبديل الحروف على النصف اليساري من المعطيات، وذلك عن طريق تطبيق تابع الحلقة F على النصف الأيمن من المعطيات. ومن ثم جمع ناتج هذا التابع مع القسم الأيسر من المعطيات بواسطة عملية XOR. يملك تابع الحلقة F نفس البنية في كل الحلقات، إلا أنه يتم تحديد عوامله بالمفتاح الجزئي k1 الخاص بكل حلقة. بعد عملية تبديل الحروف الموضحة أعلاه تنفذ عملية تبديل مواقع والتي تتكون من تبديل نصفي المعطيات فيما بينهما. تعتبر هذه البنية حالة خاصة من شبكة تبديل الحروف – تبديل المواقع (substitution-permutation network-SPN) المقترحة من قبل شانون.

يعتمد التطبيق الحقيقي لشبكة فيستيل على اختيار المعاملات وخصائص التصميم التالية: • طول الكتلة: كلما كانت الكتلة أطول كان مستوى الأمن أكبر (ومع الاحتفاظ ببقية الأمور كما هي) ولكن ذلك على حساب سرعة عمليتي التعمية وفك التعمية. يعتبر الطول 64 خانة معقولا وقد أصبح قياسا معتمدا تقريبا في تصميم نظام التشفير. على كل الأحوال طول الكتلة في خوارزمية AES الجديدة هو 128 خانة. • طول المفتاح: المفتاح الأطول يعني مستوى أمن أكبر ولكن سرعة تعمية وفك تعمية أقل. تعتبر المفاتيح ذات الطول 64 خانة أو أقل غير كافية حاليا. وبشكل عام تم اعتماد المفتاح ذو الطول 128 خانة. • عدد الحلقات: يعتمد جوهر نظام تشفير فيستيل على أن الحلقة الواحدة لا تعطي مستوى أمن كافي، غير أن تعدد الحلقات يزيد من مستوى الأمن. عدد الحلقات القياسي هو 16. • خوارزمية توليد المفاتيح الجزئية: تؤدي زيادة تعقيد هذه الخوارزمية إلى زيادة الصعوبات أمام تحليل التعمية. • تابع الحلقة F: من الواضح أنه كلما زاد تعقيد هذا التابع زادت المقاومة ضد تحليل التعمية.

هناك أيضا اعتباران آخران أثناء تصميم نظام تشفير فيستيل: • برمجيات تعمية/فك تعمية سريعة: يتم في كثير من الأحيان تضمين التعمية في التطبيقات والوظائف الخدمية ، ومن الممكن أن يتم تحقيق ذلك جهازيا، لذلك تلعب سرعة التنفيذ دورا هاما جدا. • سهولة التحليل: مع أننا نسعى لأن تكون خوارزميتنا صعبة قدر المستطاع ضد تحليل التعمية، إلا أنه من المفيد جدا جعل الخوارزمية سهلة التحليل. ذلك لأنه اذا كان بالامكان شرح الخوارزمية بسهولة وبوضوح، فإنه من السهل تحليل الخوارزمية وايجاد نقاط الضعف، وبالتالي تطويرها للحصول على مستوى أمن أعلى. لا يمكن تحليل عمل خوارزمية DES على سبيل المثال بسهولة.

بالرجوع إلى الأشكال 3-1، 3-3 نرى أن خوارزمية S-DES تبدي نفس بنية نظام فيستيل ذي الحلقتين. الفارق الوحيد عن بنية نظام فيستيل هو أن هذه الخوارزمية تبدأ وتنتهي بتابع تبديل مواقع. يظهر هذا الخلاف أيضا في خوارزمية DES الكاملة.

خوارزمية فيستيل لفك التعمية

عملية فك التعمية بنظام تشفير فيستيل هي بالمبدأ نفس عملية التعمية. والقاهدة هي كما يلي: يستخدم النص المشفر كدخل للخوارزمية، ولكن تستخدم المفاتيج الجزئية بترتيب معكوس أي يستخدم المفتاح الجزئي kn في الحلقة الأولى، kn-1 في الحلقة الثانية وهكذا حتى الحلقة الأخيرة حيث يستخدم المفتاح kl . تعتبر هذه الميزة هامة. وذلك لأننا لسنا بحاجة إلى تحقيق خوارزميتين مختلفتين، واحدة للتعمية وأخرى لفك التعمية.

وللتأكد من أن نفس الخوارزمية ولكن بترتيب مفاتيح معكوسة تعطي نتائج صحيحة سنتتبع الشكل 3-6 ، والذي يظهر عملية التعمية تسير من الأعلى إلى الأسفل في الجزء اليساري، بينما عملية فك التعمية فتنتجه من الأسفل إلى الأعلى في الجزء اليميني من الشكل، وللتوضيح فقط استخدمنا الرموز LE1 وRE1 للتعبير عن المعطيات التي تنتقل خلال خوارزمية التعمية، بينما استخدمنا الرموز LD1 وRD1 للتعبير عن المعطيات التي تتنتقل خلال خوارزمية فك التعمية. يوضح المخطط أن القيم المرحلية في حلقة عملية فك التعمية تساوي القيم الموافقة في حالة التعمية بعد تبديل الأنصاف بين بعضهما بعض. ولتوضيح ذلك بطريقة أخرى نفرض أن خرج الحلقة I من خوارزمية التعمية هو LE1||RE1 (التعبير || يعني وصل السلسلة Li بالسلسلة Ri). عندها سيكون الدخل الموافق لحلقة فك التعمية رقم (16-i) هو REi//Lei ومكافئه RD16-i||LD16. خرج هذه الحلقة هو النص المشفر النهائي. لنأخذ هذا النص ونجعله دخلا لنفس الخوارزمية. دخل الحلقة الأولى هو RE16||LE16 والذي يوافق خرج حلقة التعمية رقم 16 بعد تبديل نصفيه بين بعضهما بعض.

نريد أن نوضع الآن أن خرج حلقة فك التعمية الأولى هي في الحقيقة دخل حلقة التعمية رقم 16 بعد تبديل نصفيه بعضهما ببعض. لنأخذ أولا عملية التعمية. نرى أن:

LE16 = RE15 RE16 = LE15 ө (RE15, K16)

{{{{الشكل 3-6: التعمية وفك التعمية في نظام فيستيل}}}}

وفي جهة فك التعمية لدينا :

LD1 = RD0 = LE16= RE15 RD1 = LD0 ө F(RD0, K16) = RE16 ө F(RE15, K16) = [LE15 ө F(RE15, K16)] ө F(RE16, K16)

وبما أن عملية XOR تملك الخصائص التالية:

[A өB] ө C = A ө [B өC] D өD = 0 E ө 0 = E

نجد أن LD1 = LE15 و LD1= RE15، وبالتالي فإن خرج حلقة فك التعمية الأولى هو LE1||RE15. وهو عبارة عن دخل حلقة التعمية رقم 16 بعد تبديل نصفيه بعضهما ببعض. يسري هذا التوافق على كل الحلقات الست عشرة. يمكن تلخيص ذلك برموز عامة: فمن أجل التكرار ذي الرقم i من خوارزمية التعمية يمكن أن نكتب:

Lei = REi REi = Lei-1 ө F (REi-1, Ki)

وبإعادة ترتيب الرموز نحصل على:

REi-1 = Lei LEi-1 = REi ө F(REi-1, Ki) = REi ө F(Lei, Ki)

نكون بذلك قد عبرنا عن دخل التكرار ذي الرقم i كتابع للخرج، وتثبت هذه المعادلات التناسب المبين على الطرف اليميني من الشكل 3-6.

نرى أخيرا أن خرج الحلقة الأخيرة من عملية فك التعمية هو RE0||LE0، وهو عبارة التبديل العكسي لأنصاف النص الصريح الأساسي، وبذلك نكون قد بينا صحة عملية فك التشفير لنظام فيستيل.

لاحظ أن هذا الاستنتاج لا يتطلب أن يكون التابع F عكوسا. وللتأكد من ذلك نأخذ حالة خاصة بيحث ينتج التابع F خرجا ثابتا (على سبيل المثال واحدات) بعض النظر عن قيمة دخليه. لاحظ أن المعادلات السابقة لا تزال سارية المفعول.


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

تأريخ

Date Year Event
15 May 1973 NBS publishes a first request for a standard encryption algorithm
27 August 1974 NBS publishes a second request for encryption algorithms
17 March 1975 DES is published in the Federal Register for comment
August 1976 First workshop on DES
September 1976 Second workshop, discussing mathematical foundation of DES
November 1976 DES is approved as a standard
15 January 1977 DES is published as a FIPS standard FIPS PUB 46
1983 DES is reaffirmed for the first time
1986 Videocipher II, a TV satellite scrambling system based upon DES begins use by HBO
22 January 1988 DES is reaffirmed for the second time as FIPS 46-1, superseding FIPS PUB 46
July 1990 Biham and Shamir rediscover differential cryptanalysis, and apply it to a 15-round DES-like cryptosystem.
1992 Biham and Shamir report the first theoretical attack with less complexity than brute force: differential cryptanalysis. However, it requires an unrealistic 247 chosen plaintexts.
30 December 1993 DES is reaffirmed for the third time as FIPS 46-2
1994 The first experimental cryptanalysis of DES is performed using linear cryptanalysis (Matsui, 1994).
June 1997 The DESCHALL Project breaks a message encrypted with DES for the first time in public.
July 1998 The EFF's DES cracker (Deep Crack) breaks a DES key in 56 hours.
January 1999 Together, Deep Crack and distributed.net break a DES key in 22 hours and 15 minutes.
25 October 1999 DES is reaffirmed for the fourth time as FIPS 46-3, which specifies the preferred use of Triple DES, with single DES permitted only in legacy systems.
26 November 2001 The Advanced Encryption Standard is published in FIPS 197
26 May 2002 The AES standard becomes effective
26 July 2004 The withdrawal of FIPS 46-3 (and a couple of related standards) is proposed in the Federal Register[1]
19 May 2005 NIST withdraws FIPS 46-3 (see Federal Register vol 70, number 96)
April 2006 The FPGA based parallel machine COPACOBANA of the University of Bochum and Kiel, Germany, breaks DES in 9 days at $10,000 hardware cost.[2] Within a year software improvements reduced the average time to 6.4 days.
Nov. 2008 The successor of COPACOBANA, the RIVYERA machine reduced the average time to less than one single day.

التعمية القياسية للمعطيات

تعتمد مخططات التعمية الأكثر انتشارا على مقياس تعمية المعطيات (Data Encryption Standard-DES) والتي تم نشرها والاعتراف بها من قبل المكتب العالمي للقياسات عام 1977. تسمى الخوارزمية بحد ذاتها "بخوارزمية تشفير المعطيات " (Data Encrytion Algorithm-DEA) . يتم وفق خوارزمية DES تعمية المعطيات على شكل كتل بطول 64 خانة وباستخدام مفتاح بطول 56 خانة. تقوم هذه الخوارزمية بتحويل كتلة الدخل ذات الأربع وستون خانة عبر سلسلة من الخطوات لتعطي خرجا بطول 64 خانة أيضا. تستخدم نفس الخطوات ونفس المفتاح لعكس عملية التعمية، بمعنى آخر لفك التعمية.

لاقت خوارزمية DES انتشارا واسعا. كما أنها كانت موضوعا للجدل حول إثبات مستوى الأمن الذي تحققه. ولتبيان طبيعة هذا الجدل سنستعرض بسرعة تاريخ هذه الخوارزمية.

هيأت شركة IBM في أواخر الستينات مشروعا بحثيا حول التعمية بإشراف هورست فيستيل Horst Feistel. انتهى هذا المشروع عام 1971 بانتاج خوارزمية تعمية باسم LUCIFER ، والتي تم بيعها لشركة لويد اللندنية Lloyd’s of London للتجارة البحرية من أجل استخدامها في النظام المالي لهذه الشركة، والذي تم تطويره أيضا من قبل شركة IBM. خوارزمية LUCIFER هي عبارة عن نظام تشفير فيستيل الكتلي والذي يعمل على طول كتلة 64 خانة. ومع مفتاح بطول 128 خانة. وبسبب النتائج الواعدة لمشروع LUCIFER، قامت شركة IBM بتكثيف الجهود لتطوير منتج تعمية تجاري قابل للتسويق، بحيث يمكن تحقيقه في شريحة واحدة. قاد هذه الجهود كل من ولتر تاتشمان Walter Tachman وكارل ميير Carl Meyer، وقد عمل في هذا المشروع باحثون ومستشارون من خارج شركة IBM ومرشدين تقنيني من NSA. ناتج هذه الجهود هو نسخة معدلة من LUCIFER والتي كانت أكثر مقاومة لتحليل التعمية، ولكن كانت بمفتاح ذو 56 خانة وذلك لتضمينها على شريحة واحدة.

طرح مكتب القياسات القومي عام 1973 طلبا حول الحاجة لاعتماد نظام تشفير قياسي قومي. قدمت شركة IBM نتائج مشروع تاتشمان-ميير، وقد كانت هذه الخوارزمية الأفضل إلى حد كبير بين الخوارزميات المقدمة وقد تم اعتمادها عام 1977 كخواركية تشفير معطيات قياسية.

تعرضت هذه الخوارزمية قبل اعتمادها لأ، تكون محط انتقاد كثيف، والذي لم ينته حتى هذا اليوم. هناك ناحيتان أشعلتا الانتقاد. أولهما أن طول المفتاح لخوارزمية LUCIFER الأصلية هو 128 خانة، أما طول المفتاح في الخوارزمية المقدمة فقد أصبح 56 خانة، أي أن هناك تخفيض محسوس لطول المفتاح بطول 72 خانة. خاف المنتقدون من أن يكون المفتاح قصير جدا لمقاومة محاولات كسر التعمية بالتجريب. الناحية الثانية من الانتقاد كانت تخص البنية الداخلية لخوارزمية DES أي الصناديق S. حيث لم يكن المستخدمون متأكدين من خلو البنية الداخلية غير أن الأحداث المتلاحقة، وخاصة الأعمال الأخيرة في تحليل التعمية التفاضلي، بينت أن خوارزمية DES تملك بنية داخلية قوية. والأكثر من ذلك، صرح أعضاء IBM أن التغيير الوحيد الذي طرأ على ما قدمته الشركة هو تغيير صناديق S حسب اقتراح NSA ، وذلك لإزالة نقاط الضغف التي تم تحديدها أثناء عملية التطوير.

في جميع الأحوال، نجحت خوارزمية DES ولاقت انتشارا واسعا خصوصا في التطبيقات المالية. أعاد المعهد القومي للمقاييس والتقنيات عام 1997 (NIST) التأكيد على استخدام خوارزمية DES فيدراليا ولمدة خمسة سنوات جدد. نصح NIST استخدام خوارزمية DES للتطبيقات الأخرى. غير تلك التي تحمي المعلومات المصنفة. وفي عام 1999 طرح NIST نسخته الجديدة من المقاييس والتي أشارت إلى استخدام خوارزمية DES الثلاثية (Triple-DES) والتي تتضمن في جوهرها تكرار خوارزمية DES ثلاث مرات لنفس النص الصريح وباستخدام مفتاحين أو ثلاثة مفاتيح مختلفة وذلك لانتاج النص المشفر. سوف ندرس خوارزمية DES الثلاثية في الفصل السادس ولأن البنية التحتية لخوارزميات التعمية وفك التعمية في هذه الخوارزمية هي نفسها المستخدمة في خوارزمية DES فلا ضير من فهم الأخيرة بشكل مفصل وجيد.

التعمية وفق خوارزمية DES

يبين الشكل 3-7 البنية العامة لمخطط التعمية وفق خوارزمية DES. وكما هو الحال في أي مخطط تعمية، هناك دخلان: الأول هو عبارة عن النص الصريح المطلوب تعميته والآخر هو المفتاح. طول النصح الصريح في هذه الحالة 64 خانة، وطول المفتاح هو 56 خانة (تقبل الخوارزمية عمليا 64 خانة كمفتاح، لكن يتم استخدام 56 خانة فقط. أما الخانات الثمانية الباقية فتستخدم كخانات ازدواجية).

يمكن بالنظر إلى الطرف اليساري من الشكل ملاحظة أن معالجة النص الصريح تمر من خلال ثلاث مراحل. تمر كتلة النص الصريح ذات الطول 64 خانة في المرحلة الأولى من خلال عملية تبديل مواقع أولية (IP). والتي تعيد ترتيب الخانات. يتبع ذلك مرحلة ثانية مؤلفة من 16 حلقة لها نفس الوظيفة. والتي تتضمن تابعي تبديل حروف وتبديل مواقع. يتألف خرج الحلقة الأخيرة (السادس عشر) من 64 خانة والذي هو في الأصل تابع للنص الصريح والمفتاح معا. يتم بعد ذلك تبديل نصفي هذا الخرج مع بعضهما بعض لانتاج خرج مبدئي. يمر هذا الخرج عبر عملية تبديل المواقع (IP-1) والتي تعاكس عملية التبديل الأولى، وبذلك يتم انتاج النص المشفر النهائي . نلاحظ أن خوارزمية DES تملك نفس بنية نظام تشفير فيستيل والمبينة في الشكل 3-5، ولكن بعد استثناء عمليتي التبديل الأولى والثانية.

يبين القسم الأيمن من الشكل 3-7 طريقة استخدام المفتاح ذو الطول 56 خانة. يمر المفتاح عبر تابع تبديل مواقع. يتم بعد ذلك انتاج مفتاح جزئي k1 من أجل كل مرحلة من المراحل الست عشرة، وذلك عن طريق تطبيق وظيفتين متتاليتين هما ازاحة دائرة يسارية وتبديل مواقع. عملية تبديل المواقع متناظرة في كل المراحل، إلا أنه يتم انتاج مفاتيح مختلفة نتيجة الازاحة المتكررة لخانات المفتاح.

{{{{الشكل 3-7: الوصف العام لخوارزمية تعيمة DES}}}}}

عملية التبديل الأولية

يتم تحديد عميليتي التبديل الأولى ومعاكستها عن طريق الجدوال 3.2b, 3.2a على التوالي. يمكن تفسير هذه الجدوال كما يلي: يتألف الدخل من 64 خانة يتم ترقيمها من 1 وحتى 64. تحوي المداخل الأربعة والستون من جدول تبديل المواقع أرقام الخانات البديلة من 1 وحتى 64. أي أن كل خلية في جدول تبديل المواقع تشير إلى موقع خانة الدخل التي ستشكل خانة الخرج.

لإظهار أن تابعي تبديل المواقع هما في الحقيقة عكس بعضهما البعض سندرس خانات الدخل M، التالية والتي عددها 64:

M8 M7 M6 M5 M4 M3 M2 M1 M16 M15 M14 M13 M12 M11 M10 M9 M24 M23 M22 M21 M20 M19 M18 M17 M32 M31 M30 M29 M28 M27 M26 M25 M40 M39 M38 M37 M36 M35 M34 M33 M48 M47 M46 M45 M44 M43 M42 M41 M56 M55 M54 M53 M52 M51 M50 M49 M64 M63 M62 M61 M60 M59 M58 M57

حيث M1 هي عبارة عن خانة ثنائية. عندها يمكن وصف تبديل المواقع X = IP(M) كما يلي:

M2 M10 M18 M26 M34 M42 M50 M58 M4 M12 M20 M28 M36 M44 M52 M60 M6 M14 M22 M30 M38 M46 M54 M62 M8 M16 M24 M32 M40 M48 M56 M64 M1 M9 M17 M25 M33 M41 M49 M57 M3 M11 M19 M27 M35 M43 M51 M59 M5 M3 M21 M29 M37 M45 M53 M61 M7 M15 M23 M31 M39 M47 M55 M63

اذا أخذنا بعد ذلك تبديل المواقع العكسي Y = IP-1(X) = IP-1(IP(M))، عندها يمكن التبيان أنه ستتم استعادة الترتيب الأصلي.

تفصيلات حلقة واحدة

يبين الشكل 3-8 البنية الداخلية لكل حلقة. لنبدأ مرة أخرى بالتركيز على الطرف اليساري من المخطط. تتم معالجة النصفين اليساري واليمين لكل 64 خانة مرحلية كقيم منفصلة ذات 32 خانة مرمزة بالشكل L (يساري) وR (يميني). وكما هو الحال في أي نظام تشفير فيستيل تقليدي، يمكن تلخيص المعالجة الكلية لكل حلقة بالمعادلات التالية:

Li = Ri-1 (1-3) Ri = Li-1 ө F(Ri-1, k1) (2-3)

الجدول3-2: جدول تبديل المواقع لخوارزمية DES

يتألف مفتاح كل حلقة من 48 خانة. الدخل R مؤلف من 32 خانة. يتم توسيع الدخل R إلى 48 خانة باستخدام الجدول 3-2C الذي يحدد عمليتي تبديل مواقع وتوسيع بنفس الوقت. والذي يتضمن تكرار 16 خانة من خانات الدخل R. يتم بعد ذلك جمع الخانات الثماني والأربعون الناتجة مع المفتاح الجزئي k1 عن طريق XOR. يتم تمرير الخانات الثماني والأربعين الناتجة عبر تابع تبديل حروف والذي ينتج خرجا بطول 32 خانة، والتي يتم اعادة ترتيبها عن طريق الجدول 3-2d.

الشكل 3-8: حلقة واحدة من خوارزمية DES

يبين الشكل 3-9 دور الصناديق S في التابع F. تتألف عمليتي تبديل الحروف من مجموعة مؤلفة من ثمانية صناديق S، يقبل كل منها ست خانات دخل وينتج أربع خانات خرج. يتم تحديد هذه التحويلات في الجدول 3-3، والذي يتم تفسيره كما يلي: تشكل الخانات الأولى والأخيرة من دخل الصندوق Si رقما ثنائيا مؤلفا من خانتين والذي يحدد واحدة من أربع عمليات تبديل حروف معرفة بواسطة أربعة أسطر من جدول الصندوق Si. بينما تساعد الخانات الأربع الوسطى على اختيار أحد الأعمدة الستة عشر. تحوي الخلية الواقعة على تقاطع السطر والعمود المختارين قيمة عشرية. القيمة الثنائية المؤلفة من أربع خانات عن تحويل هذه القيمة العشرية هي بالحقيقة الخرج المطلوب. فعلى سبيل المثال اذا كان دخل صندوق si هو 011001، عندها سيكون السطر المختار هو السطر ذي الرقم 01 (السطر الأول)، والعمود المختار هو العمود ذو الرقم 1100 (العمود رقم 12) . الخلية الواقعة على تقاطع السطر الأول والعمود رقم 12 تحوي القيمة 9، أي أن الخرج هو 1001.

يحدد كل سطر من الصندوق S عملية تبديل حروف عكوسة. يمكن أن يساعد الشكل 3-4 على فهم عملية التحويل. يبين الشكل عملية تبديل الحروف للسطر رقم 0 من الصندوق Si.

يستحق عمل صناديق S تعليقات أكثر. لنهمل حاليا تأثير المفتاح k1. اذا تفحصت جدول التوسيع سترى أنه تم تقسيم خانات الدخل الاثنتين والثلاثين إلى مجموعات ذات أربع خانات، تصبح بعد ذلك مجموعات ذات ست خانات عن طريق تكرار الخانات الخارجية لكل مجموعتين متتاليتين. فعلى سبيل المثال اذا كانت العبارة التالية جزءا من كتلة الدخل.

….efgh ijkl mnop….

عندها ستصبح بعد التحويل:

…..defghi hijklm lmnopq ….


الشكل 3-9: حساب التابع F (R,K.

تساعد الخانتان الخارجيتان من كل مجموعة على اختيار واحدة من أربع حالات تبديل حروف محتملة (سطر ويحد في الصندوق S). يتم بعد ذلك تبديل أربع خانات الدخل (الخانات الأربع الوسطى) بأربع خانات خرج. تطبق بعد ذلك عملية تبديل حروف على الخانات الإثنتين والثلاثين الناتجة عن صناديق S الثمانية، وبذلك سيؤثر خرج كل صندوق S، مباشرة على مداخل الحلقة التالية.


الجدول 3-3: تعريفات صناديق s في خوارزمية DES


يمكن التعبير عن مخطط التعمية وفق خوارزمية DES كما يلي: • الدخل: النص الصريح M= m1, m2 ….m64 ومفتاح بطول 64 خانة K = k1, k2, l3 …k64 (يضم ثماني خانات ازدواجية). • الخرج: نص مشفر بطول 64 خانة C = c1, c2 … c64. • الإجرائية:

1- (توليد المفاتيح( يتم توليد 16 مفتاحا جزئيا k1 للحلقات، طول كل منها 48 خانة، وذلك باستخدام مخطط توليد المفاتيح الوارد في الفقرة التالية. 2- IP (m1, m2 …m64) → (L0, R0) . يستخدم لذلك التبديل IP المبين في الجدول 3-2a وذلك لتبديل مواقع الخانات. ومن ثم تقسم النتيجة إلى نصفين يميني ويساري كل منهما بطول 32 خانة R0 = m57, m49 … m7 و L0 = m58, m50 …m8. 3- يتم تنفيذ 16 حلقة متناظرة بحيث يتم حساب R1, L1 (حيث 1 ≤ i ≤ (16 وذلك باستخدام المعادلات 3.1 و 3.2. يتم حساب F(Ri-1, Ki) = P(E(Ri-1)ө Ki)) كما يلي: أ‌- نوسع Ri-1 = r1, r2, r3, …r52 من 32 خانة وذلك باستخدام وظيفة التبديل – التوسيع E المبينة في الجدول 3-2C:

(T = r32 r1 r2 .. r32 r1) E(Ri-1) → T

ب‌- T ө K1 → T تكتب T على شكل ثماني سلاسل كل منها حرف بست خانات ، T = (B1, ….B8). ج – (S1(B1), S2(B2) .. S8(B8)، حيث تحول الوظائف S1(B1) كل سلسلة Bi = b1 b2 …b6 إلى قيمة بأربع خانات موجودة بشكل عشري في السطر r والعمود c من الصندوق Si الموضح في الجدول 3-3، حيث b2 b3 b4 , r = 2.b1 + b6 هي التمثيل الثنائي لرقم العمود C (أي 0 ≤ c≤15). وبالتالي فإن (011011) Si سوف تعطي r = 1 , c = 13 وقيمة الخرج هي 5 أو مكافئها الثنائي (0101). د- P(T) → T يستخدم لذلك الجدول 3-2d. وذلك لتبديل مواقع الخانات الاثنتين والثلاثين الناتجة عن T.

4- (R16, L16) → b1 b2 … b64. (يتم تبديل الكتل النهائية R16, L16 فيما بينهما). 5- IP-1(b1 b2 … b64). يستخدم لذلك التبديل IP-1 الموضح في الجدول 3-2b، (أي C= b40 b 8 … b25).


توليد المفاتيح

بالعودة إلى الأشكال 3-7 و 3-8 نجد أن المفتاح ذا الطول 64 خانة هو دخل الخوارزمية. يتم ترقيم خانات المفتاح من 1 وحتى 64. يتم اهمال كل خانة ثامنة وذلك كما هو مشار غليه في الجدول 3-4a. وهو ما يميز عملية التبديل الموضحة في جدول خيار التبديل الأولي (Permuted Choice One) الموضح في الجدول 3-4b. تتم معالج المفتاح ذي الست والخمسين خانة بعدئذ على شكل نصفين كل منهما 28 خانة، مرمزين D0, C0. تنفذ عملية ازاحة دورانية يسارية في كل دورة على Di-1, Ci-1 بشكل مستقل، إما لخانة واحدة أو لخانتين كما هووارد في الجدول 3-4d. تصبح هذه القيم المزاحة دخل الحلقة التالية. كذلك تصبح دخلا لخيار التبديل الثاني Permuted Choice Two والذي ينتج خرجا بطول 48 خانة يعطي بدوره للتابع P(Ri-1, Ki).

يمكن بشكل عام التعبير عن مخطط توليد المفاتيح كما يلي:

• الدخل: مفتاح ذو 64 خانة K = k1 k2 … k64 يضم ثماني خانات ازدواجية. • الخرج: ستة عشر مفتاحا K1 طول كل منها 48 خانة، حيث 1 ≤ I ≤ 16. • الإجرائية: 1- تعرف v1، حيث 1 ≤ i ≤ 16، كما يلي: v1 = 1 من أجل i ε {1, 2, 9, 16} و v1 = 2 من أجل بقية قيم i (هذا ما سيمثل عدد خانات الإزاحة اليسرى الدورانية لكل 28 خانة). 2- PC1 (K) → T يتم تمثيل T على شكل نصفين (C0, D0) يتألف كل منهما من 28 خانة. (يستخدم لذلك التبديل PC1 المبين في الجدول 3-4b وذلك لاختيار الخانات من C0 = K56 K49 .. K26 و D0= K63 K55 .. K4). 3- نحسب K1، من أجل 1 ≤ i ≤ 16، كما يلي: Ki , Di ← (Di-1 <<< vi), Ci ← (Ci-1 >>> vi) ← PC2 (Ci, Di) (يستخدم التبديل PC2 المبين في الجدول 3-4C لاخيتار 48 خانة نتيجة وصل السلاسل b1 b2 b2 .. b56 و (Ki= b14 b17 … b32 – الرمز >>> يعبر عن ازاحة دورانية بمقدار vi.

فك التعمية وفق خوارزمية DES

تستخدم عملية فك التعمية ، كما هو الحال في أي نظام تشفير فيستيل، نفس خوارزمية التعمية ، ما عدا أن ترتيب المفاتيح الجزئية سيكون مقلوبا.

{{{الجدول 4-3: مخطط توليد المفاتيح في خوارزمية DES{}}}}

تأثير الانهيار الثلجي – أو التأثير التراكمي

الخاصية المستحبة أو المرغوب بها في أي خوارزمية تعمية هي تأثير النص المشفر بشكل كبير عند حدوث أي تغير بسيط في النص الصريح أو في المفتاح. وبشكل خاص، تغيير خانة واحدة في النص الصريح أو في المفتاح يجب أن تنتج تغييرا في خانات كثيرة من النص المشفر، أما اذا كان التغير الناتج صغيرا، فربما سيؤدي ذلك إلى إيجاد طريقة لتقليص حجم النص الصريح، أو مجال المفاتيح الذي يتم البحث فيه.

تتميز خوارزمية DES بتاثير انهياري قوي. يبين الجدول 3-5 بعض نتائج الاحصائيات الدراسية. تم استخدام نصان صريحان مختلفان بخانة واحدة في الجدول 3-5a:

00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 10000000

والمفتاح المستخدم هو:

0110010 0011100 0011000 0011100 1100010 0100100 1001011 00000001

يبين الجدول أنه بعد الحلقة الثالثة فقط سيكون الخلاف بين الكتلتين هو 21 خانة. وبعد نهاية كل الحلقات سيصبح عدد الخانات المختلفة هو 34 خانة.

يبين الجدول 3-5b نفس الاختيار ولكن عند استخدام نص صريح واحد هو:

10100100 11101011 01110110 00010011 01111010 00101111 10000101 01101000

بينما يتم استخدام مفتاحين مختلفين بخانة واحدة:

1101110 0110001 0000100 0011101 0011000 1101111 1111011 1110010 1101110 0110001 0000100 00111001 0011000 1101111 1111011 0110010

تبين النتائج مرة أخرى بأنه حوالي نصف الخانات في النص المشفر سوف تتغير وأن التأثير الانهياري سيكون ملحوظا بعد بضع دورات فقط.

الجدول 3-5: التأثير الانهياري في خوارزمية DES: 

(a) تغيير في النص الصريح	 (b) تغيير في المفتاح

0 1 0 0 1 6 1 2 23 21 23 14 4 35 4 28 5 39 5 32 6 34 6 30 7 32 7 32 8 31 8 6 9 29 9 34 10 42 10 40 11 44 11 38 12 32 12 31 13 30 13 33 14 30 14 28 15 26 15 26 16 29 16 34 34 34


قوة خوارزمية DES

بقيت خوارزمية DES منذ اعتمادها على الصعيد الحكومي محط الاهتمام للتحقق من مستوى الأمن الذي تحققه. وقد توزع هذا الاهتمام على مجالين: الأول هو طول المفتاح، والثاني هو طبيعة الخوارزمية بحد ذاتها.

استخدام مفاتيح بطول 54 خانة

عندما يكون طول المفتاح 56خانة فإن هذا يعني أن هناك 556 مفتاحا مختلفا، أو ما يقارب 1016 X 7.2 مفتاحا مختلفا. نستنتج من هذا أن محاولة كسر المفتاح عن طريق "الهجوم الأعمى" (التجريب) غير عملية نهائية. فاذا افترضنا أنه يجب تجريب حوالي نصف عدد المفاتيح للوصول إلى المفتاح المطلوب، وبفرض أن الحاسب الواحد يستغرق حوالي 1 ميكرو ثانية فقط لانجاز عملية فك تشفير باعتماد خوارزمية DES، فسنجد أن عملية الكسر سوف تستغرق أكثر من 1000 سنة (انظر الجدول 2-2). لكن الافتراض أن عملية التعمية أو فك التعمية تستغرق حوالي 1 ميكروثانية، هو افتراض مبالغ فيه وقد تم عرضه للتوضيح فقط. افترض Diffie و Hellman بأن التقنية الموجودة كفيلة ببناء حواسب متوازية، مزودة بمليون جهاز تعمية، يستطيع كل منها تنفيذ عملية التعمية بحوالي ميكروثانية واحدة، يمكن بذلك تخفيض الزمن اللازم إلى حوالي عشرة ساعات. أما كلفة ذلك فقد قدر بحوالي 20 مليون دولار عام 1977.

ثبت أخيرا وبشكل قاطع عام 1998 عدم سرية النظام DES ، وذلك عندما أعلنت احدى الشركات عن كسر خوارزمية DES باستخدام طريقة خاصة أسمتها "آلة كسر DES" DES cracker machine والتي تم بناؤها بأقل من 250 ألف دولار. استغرقت عملية الكسر أقل من ثلاثة أيام. وقد نشرت هذه الشركة وصفا مفصلا عن هذه الآلة، سامحة بذلك للآخرين ببناء مثل هذه الآلة. وبما أن سعر الحواسب ينخفض بسرعة كبيرة مع زيادة سرعتها، نجد أن خوارزمية DES أصبحت الآن بلا قيمة عملية.

من المهم ملاحظة أن الكثير يتعلق بأسلوب البحث عن المفتاح بدلا من تجريب كل المفاتيح المحتملة. فاذا لم يكن النص الصريح معروفا، عندها يجب على المحلل أن يمتلك القدرة على التعرف على النص الصريح. فاذا كانت الرسالة هي عبارة عن نص إنجليزي فحسب، فإن التعرف عليها يصبح سهلا، ومع ذلك يجب أن تتم أتمتة عملية التعرف على النصوص الإنجليزية. أما اذا تم ضغط الرسالة قبل تعميتها، عندها سيكون التعرف عليها أصعب. واذا كانت الرسالة عبارة عن أحد أنواع المعطيات المتداولة، وتم ضغطها قبل التعمية، فإن المشكلة ستتعقد أكثر، وستصبح أتمتة عملية التعرف على النص شبه مستحيلة. أي أن استخدام طريقة الهجوم الأعمى يتطلب وجودة معرفة ما حول النص الصريح المتوقع، هذا بالاضافة إلى نوع ما من أتمتة عملية التعرف على النصوص. قدمت الشركة التي كسرت خوارزمية DES حلولا لهذه المسألة أيضا، بالاضافة إلى تقنيات مؤتمتة لزيادة فعالية الكسر بالاضافة إلى مواضيع مختلفة أخرى متعلقة بعمليات الكسر.

لحسن الحظ هناك العديد من بدائل DES، أهمها خوارزمية AES وخوارزمية DES الثلاثية والتي سيتم شرحها في الفصلين الخامس والسادس على التوالي.

طبيعة خوارزمية DES

هناك ناحية أخرى تسبب القلق وهي الاحتمالات الممكنة لتحليل التعمية عن طريق السيطرة على خصائص خوارزمية DES . ركز هذا الاهتمام بشكل خاص على جدوال التبديل أو ما يسمى صناديق S، والتي تستخدم في كل دورة. نتيجة للخصائص التصميمية فهذه الصناديق بشكل خاص وللخوارزمية ككل بشكل عام، والتي لم تنشر للعوام، هناك شك بأنه قد تم تصميم هذه الصناديق بشكل يجعل تحليل التعمية ممكنا بالنسبة للمهاجم الذي يعرف نقاط الضعف الخاصة بهذه الصناديق. ومع مرور الوقت تم اكتشاف قوانين هذه الصناديق والتصرفات غير المتوقعة لها. وعلى الرغم من ذلك، لم يتسنى لأحد اكتشاف نقاط الضعف القاتلة والمتوقعة لهذه الصناديق.

الهجوم الزمني

سندرس الهجوم الزمني بشكل أكثر تفصيلا في القسم الثاني من هذا الكتاب، حيث أنها تنسب إلى خوارزميات المفتاح العمومي. على كل الأحوال يمكن طرح هذه المشكلة في خوارزميات التعمية بالفتاح المتناظر. الهجوم الزمني في الجوهر هو ذلك الهجوم الذي يتم من خلاله الحصول على معلومات حول المفتاح أو النص الصريح من خلال مراقبة الزمن اللازم في تطبيق ما لانجاز عمليات فك تعمية لنصوص مشفرة مختلفة. يستغل الهجوم الزمني حقيقة أن خوارزميات التعمية وفك التعمية تستغرق أزمنة تختلف عن بعضها قليلا عند اختلاف الدخل. هناك بعض الطرق التي تعطي أوزان هامينغ (أرقام الخانات المساوية للواحد) للمفتاح السري. وهو شوط كبير باتجاه معرفة المفتاح الحقيقي. إلا أن الخبراء خلصوا إلى نتيجة مفادها أن خوارزمية DES مقاومة جدا للهجوم الزمني، مع أنهم اقترحوا بعض الأساليب التي قد تساهم في انجاح الهجوم الزمني. ومع أن هذا النوع من الهجوم فعال أحيانا، إلا أنه لن يكون ناجحا أبدا مع خوارزمية DES أو مع خوارزميات التعمية بالمفتاح المتناظر القومية مثل خوارزمية DES الثلاثية أو خوارزمية AES.

تحليل التعمية التفاضلي والخطي

التساؤل الأول، على طول حياة خوارزمية DES، هو حول مدى ضعف هذه الخوارزمية تجاه الهجوم الأعمى، وذلك نتيجة لقصر طول المفتاح (56 خانة). لكن كان هناك أيضا اهتمام في ايجاد طريقة الهجوم على خوارزمية DES باستخدام تحليل التعمية. ومع زيادة شعبية نظم التعمية الكتلية ذات المفاتيح الطويلة، بما في ذلك خوارزمية DES الثلاثية، أصبح الهجوم الأعمى غير فعال. لذلك ازداد التأكيد على ايجاد طرق هجوم على خوارزمية DES وعلى بقية أنظمة التعمية المتناظرة باستخدام تحليل التعمية. سنقدم في هذا المقطع نظرة مختصرة على أكثر طريقتين فعالتين وواعدتين: تحليل التعمية التفاضلي، وتحليل التعمية الخطي.


تحليل التعمية التفاضلي

يعتبر تحليل التعمية التفاضلي واحدا من أهم التطورات التي طرأت على تحليل التعمية في السنوات الأخيرة. سنناقش في هذا المقطع هذه التقنية وتطبيقاتها على خوارزمية DES.

تاريخ

لم يتم نشر أي شئ حول تحليل التعمية التفاضلي حتى عام 1990. وأول جهود تم نشرها كانت متعلقة بتحليل التعمية لخوارزمية التشفير المدعوة FEAL وذلك من قبل Murphy. بعد ذلك ظهرت سلسلة من النشرات لكل من Shamir , Biham والتي بينت هذا النوع من الهوم على عدد من خوارزميات التعمية وتوابع المزج والتوزيع (has function).

النتائج الأكثر انتشارا لهذه المواضيع هي تلك التي تطبق على خوارزمية DES. يعتبر تحليل التعمية التفاضلي أول هجوم تم نشره يحقق كسر خورازمية DES بأقل من 255 حالة. يمكن أن ينجح كسر خوارزمية DES عند استخدام تحليل التعمية التفاضلي بجهود من مرتبة 247 محتاجين بذلك إلى 247 نص صريح مختار. ومع أن القيمة 247 أقل بكثير من القيمة 255 ، إلا أن هذا النوع من الهجوم يبقى للدراسات النظرية فقط، والسبب في ذلك هو الحاجة إلى 247 نص صريح مختار.

ومع أن تحليل التعمية التفضالي يعتبر أداة قوية، إلا أنه لم يؤثر بشكل جيد على خوارزمية DES ويعود السبب في ذلك، حسب ما أدلى به عضو فريق IBM الذي صمم هذه الخوارزمية، إلى أن تحليل التعمية التفاضلي عرف من قبل الفريق عام 1974، حيث لعبت الحاجة إلى تقوية خوارزمية DES ضد الكسر باستخدام التحليل التفاضلي دورا كبيرا في تصميم صناديق S وعملية تبديل المواضع P. وكدليل على هذا الدور سنطرح المقارنة التالية: يحتاج تحليل التعمية التفاضلي لخوارزمية LUCIFER ذات الثماني مراحل إلى 256 نص صريح مختار، بينما يتطلب الهجوم على نموذج من خوارزمية DES بثماني مراحل أيضا إلى 214 نص صريح مختار.

الهجوم باستخدام تحليل التعمية التفاضلي

يعتبر الهجوم باستخدام تحليل التعمية التفاضلي أمرا معقدا، سنكتفي هنا بعرض نظرة مختصرة تفيد في تقديم هذه الطريقة للكسر. أما اذا اردت تفصيلا لها فيجب الرجوع إلى المراجع المختصة بها.

سنبدأ بتغيير الوصف الخاص بخوارزمية DES. اذا افترضنا أن كتلة النص الصريح هي m والمؤلفة من النصفين m0, m1، يجري في كل مرحلة نقل نصف الدخل الأيمن إلى نصف الخرج الأيسر، أما نصف الخرج الأيمن فيكون نتيجة تابع دخله نصف الدخل الأيسر والمفتاح الجزئي الخاص بهذه المرحلة. لذلك سيتم في كل مرحلة انتاج كتلة جديدة بطول 32 خانة فقط. اذا أعطينا كل كتلة جديدة الرمز m1 (حيث 7 ≥ i ≥ 2)، عندها سيكون أنصاف الرسالة المرحلية مرتبطين بالشكل:

Mi+1 = mi-1 ө F(mi, Ki I = 1, 2, 3, …. 16

نبدأ في تحليل التعمية التفاضلي بالرسالتين m1, m مع معرفة فارق XOR بينهما، أي ∆ m = m ө m1 ، وليكن الفارق بين أنصاف الرسالة المرحلية هو ∆ m = m ө m11، عندها يكون لدينا:

∆ mi-1 = mi+1 ө m1i-1 = [mi-1 ө F(mi, ki)] ө [mi-1 ө F(mi-, ki)] = ∆mi-1 ө [F(mi, ki) ө f(mi, ki)]

لنفترض الآن بأن عدة أزواج من الدخل التابع f وبنفس الفارق تعطي نفس الفارق في الخرج اذا تم استخدام نفس المفتاح الجزئي. ولطرح ذلك بشلك أدق سنقول بأن X يمكن أن تنتج Y باحتمال مقداره P اذا كان الكسر P يميز كل الأزواج التي يكون من أجلها دخل XOR هو X وخرج XOR هو Y. لنفترض ان هناك عددا من القيم X التي تعطي باحتمال كبير فرقا معينا في الخرج. لذلك، اذا علمنا ∆ mi-1, ∆ mi باحتمال كبير، عندها يمكن معرفة ∆ mi-1 باحتمال كبير أيضا. والأكثر من ذلك، اذا أمكن تحديد عدد هذه الفروق فمن المحتمل تحديد المفتاح الجزئي المستخدم كدخل للتابع f.

تعتمد الاستراتيجية العامة لتحليل التعمية التفاضلي على هذه الاعتبارات لمرحلة واحدة. وتتلخص الاجرائية بالبدء بنصين صريحين m, m1 وفرق معطى، ومتابعتهما خلال نموذج محتمل من الفروقات بعد كل مرحلة وذلك لانتاج فرق محتمل للنص المشفر. عمليا هناك فرقان محتملان للنصين المؤلفين من 32 خانة (∆ m17||∆ m16). نخضع بعد ذلك m1, m للتعمية من أجل تحديد الفرق الحقيقي تحت مفتاح غير معروف ونقارن النتيجة مع الفرق المحتمل . اذا كان هناك تطابق، أي:

Ek (m) ө Ek (m1) = ∆ m17||∆m16

عندها نشك بأن كل النماذج المحتملة في كل المراحل هي صحيحة. يمكن مع هذا الافتراض أن تجرى بعض التخمينات حول خانات المفتاح. يجب تكرار هذه الاجرائية عدة مرات لاستنتاج كل خانات المفتاح.

يوضح الشكل 3-10 كيفية توليد الفروقات لثلاث مراحل من خوارزمية DES. تشير الاحتمالات الموضحة على اليمين إلى الاحتمالات التي يمكن أن تظهرها مجموعة معطاة من الفروقات كتابع لفروقات الدخل. أخيرا، كما هو مبين، فإن احتمال فرق الخرج بعد ثلاثة مراحل يساوي 0.25X1X0.25 = 0.0625.

{{{{الشكل 3-10: التوليد التفاضلي خلال ثلاث مراحل من خورازمية DES (الأرقام مكتوبة بالست عشري}}}}}

تحليل التعمية الخطي

أتى هذا النوع من التحليل بعد تحليل التعمية الفاضلي . يعتمد هذا الهجوم على ايجاد تقريب خطي لوصف عمليات التحويل التي تتم في خوارزمية DES. يمكن لهذه الطريقة أن توجد مفتاح DES من خلال 247 نص مختار في تحليل التعمية التفاضلي . ومع أن هذا يعتبر تحسينا أساسيا، ذلك لأنه من الأسهل الحصول على نصوص صريحة معروفة بدلا من نصوص صريحة مختارة، إلا أن هذا العدد يبقى تحليل التعمية الخطي غير عملي لكسر خوارزمية DES. لذلك تم القيام بأعمال قليلة لتحقيق الكسر باستخدام تحليل التعمية الخطي.

سنوضح فيما يلي باختصار المبادئ التي اعتمد علهيا تحليل التعمية الخطية. ليكن لدينا نظام تشفير ما، والذي يكون فيه طول النص الصريح هو n خانة، أما طول المفتاح فهو m خانة. ولنرمز لكتلة النص الصريح P[1] ..P [n] ، بينما نرمز لكتلة النص المشفر C [1]..C[n]، أما المفتاح فسيأخذ الرمز K[1]…K[m] ، لنعرف بعد ذلك ما يلي:

A[I, j…k] = A[i] ө A[j] ө …+ A[k]

يهدف تحليل التعمية الخطي إلى ايجاد معادلة خطية من الشكل:

P[α1, α2…. Αa] ө C[β1, β2….βb] = K[γ1, γ2 …γc]

(حيث X تساوي 0 أو 1، 1≤C≤m، وحيث الرموز α و β و γتمثل مواقع خانات منفردة وثابتة)، يجب أن تكون هذه المعادلة محققة بالاحتمال P والذي لا يساوي 0.5. كلما بعد P عن القيمة 0.5 كلما كانت المعادلة أكثر كفاءة.

فاذا تم تحديد العلاقة المقترحة، عندها ستصبح الاجرائية هي حساب نتائج الطرف اليساري للمعادلة السابقة وذلك من أجل عدد كبير من أزواج النص الصريح-النص المشفر. اذا كانت النتيجة مساوية للصفر لأكثر من النصف عندها نفترض أن K[γ1, γ2 .. γc] = 0. اذا كانت النتيجة مساوية للواحد معظم الوقت، عندها نفتراض أن K[γ1, γ2 … γc] = 1. مما يعطينا معادلة خطية لحساب خانات المفتاح.

مبادئ تصميم نظم التشفير الكتلي

حدث تقدم كبير في مجال تصميم نظم التشفير الكتلية القوية من وجهة نظر التعمية، إلا أن المبادئ الأساسية للتصميم لم تتغير منذ تارخي عمل فيستيل وفريق تصميم خوارزمية DES أي منذ بداية السبعينات. من المفيد بدء هذه المناقشة بالتمعن فيما تم نشره حول معايير التصميم المستخدمة عند تصميم DES بعد ثلاثة مواضيع حساسة لتصميم نظام التشفير الكتلي: عدد المراحل، تصميم التابع f، وطريقة استنتاج المفاتيح.

معايير تصميم DES

تركز المعايير المستخدمة لتصميم خوارزمية DES على تصميم صناديق S والتابع P الذي يأخذ خرج الصناديق S (الشكل 3-9). معايير الصناديق S:

1- يجب ألا تكون أية خانة خرج من أي صندوق S قريبة جدا من ناتج تابع خطي ما دخله خانات الدخل. وبالتحديد اذا اخترنا أية خانة خرج وأية مجموعة جزئية من خانات الدخل الستة، فان قيمة الجزء الناتج عن قيم الدخل التي تكون من أجلها قيمة هذه الخانة من الخرج مساوية لناتج عملية XOR على الخانات من الدخل، يجب ألا تكون قريبة من الواحد أو من الصفر، بل يجب أن تكون حوالي 0.5. 2- يجب أن يحتوي كل سطر من الصندوق S (والمحدد من خلال الخانتين الأكثر أهمية والاقل أهمية من خانات الدخل) على كل تشكيلات الخرج المحتملة والبالغ عددها 16. 3- اذا اختلفت قيمتا دخل الصندوق S بخانة واحدة فقط، عندها يجب أن تختلف قيم الخرج بخانتين على الأقل. 4- اذا اختلف دخلان اثنان إلى الصندوق S في قيم الخانتين الواقعتين في الوسط بالضبط، عندها يجب أن تختلف قيم الخرج بخانتين على الاقل. 5- اذا اختلف دخلان اثنان إلى الصندوق S في أول خانتين وكانت الخانتان الأخيرتان متناظرتين، عندها يجب أن تكون قيمتا الخرج متاينتين. 6- من أجل أية قيمة فرق غير صفرية مؤلفة من 6 خانات بين قيم الدخل، يجب ألا يتواجد أكثر من ثمانية أزواج دخل (من بين كل أزواج النص البالغ عددها 32)، والتي تنتج هذا الفارق، تؤدي إلى نفس الفارق في الخرج. 7- هذا المعيار شبيه بالذي قبله ولكن من أجل ثلاثة صناديق S.

أشار كوبرسميث إلى أنه يجب تحقيق المعيار الأول من القائمة السابقة وذلك لأن صناديق S هي الجزء الوحيد غير الخطي في خوارزمية DES. فلو كانت الصناديق S خطية (أي أمكن استخراج خانة الخرج من خلال علاقة خطية تربط خانات الدخل)، لكانت كل الخوارزمية خطية ولأمكن كسرها. يمكن ملاحظة هذه الظاهرة في نظام تشفير هيل والذي يعتبر نظاما خطيا. تساعد بقية المعايير بشكل أساسي في مقاومة تحليل التعمية التفاضلي وفي تقديم خاصة بعثرة جيدة.

أما معايير تابع تبديل المواضع P فهي:

1- يتم توزيع خانات الخرج الأربع من كل صندوق S في المرحلة i بحيث تؤثر خانتان منهما (تكون دخلال) على الخانات الوسطة للمرحلة i+1 ، أما الخانتان الباقيتان فتؤثرن على الخانات النهائية. لا تكون خانتا الدخل الوسطى في دخل صندوق S مشتركتين بين صناديق S المجاورة. الخانات النهائية هي الخانتان الواقعتان إلى أقصى اليسار والخانتان الواقعتان إلى أقصى اليمين والتي تتم بالمشاركة عليها مع صناديق S المجاورة. 2- تؤثر خانات الخرج الأربعة من كل صندوق S على ستة صناديق S مختلفة في المرحلة التالية، ولا يمكن أن تؤثر اثنتان منهما على نفس الصندوق S. 3- ليكن لدينا صندوقي S التالييت k, j. اذا أثرت خانة خرج من الصندوق si على خانة وسطى من الصندوق sk في المرحلة التالية، عندها لا يمكن أن تؤثر خانة خرج من الصندوق sk على خانة وسطى من الصندوق Si . وهذا يقتضي أنه من أجل j=k، فإن خانة خرج من Si لا يمكن أن تؤثر على خانة وسطى من Sj.

تهدف هذه المعايير بمجملها إلى زيادة البعثرة في الخوارزمية.

عدد المراحل

تنبع قوة التعمية في نظام تشفير فيستيل من ثلاث نقاط تصميمية: عدد المراحل، التابع f، وطريقة استخراج المفاتيح. لنلق نظرة أولا على طريقة اختيار عدد المراحل.

كلما كان عدد المراحل أكبر كلما تعقد انجاز تحليل التعمية، حتى ولو كان التابع f، ضعيفا نسبيا. وبشكل عام يجب أن يكون المعيار هو أن يتم اختيار عدد المراحل بحيث يتطلب تحليل التعمية المعروف جهودا أكبر من تلك المصروفة على الهجوم بالبحث عن المفتاح بطريقة "الكسر الأعمى" البسيطة. تم استخدام هذا المعيار بالتأكدي أثناء تصميم خوارزمية DES. لا حظ Schneier بأنه من أجل خوارزمية DES ذات 16 مرحلة يكون الكسر باستخدام تحليل التعمية التفاضلي أقل كفاءة بقليل من الكسر بطريقة الكسر الأعمى 255 عملية. اذا تضمنت خوارزمية DES 15 مرحلة أو أقل فان تحليل التعمية التفاضلي يتطلب جهودا أقل من طريقة البحث عن المفتاح بطريقة الكسر الأعمى.

يعتبر هذا المعيار هاما لأنه يسمح بسهولة الحكم على قوة الخوارزمية وبالتالي مقارنة الخوارزميات. في حال غياب الاختراق بواسطة تحليل التعمية، يتم الحكم على قوة الخوارزمية من خلال طول المفتاح.

تصميم التابع f

يعتبر التابع f قلب نظام فيستيل للتشفير الكتلي. يعتمد هذا التابع، كما رأينا، على استخدام الصناديق S.وهذ هي حالة معظم أنظمة التشفير الكتلي المتناظر، كما سنرى في الفصل السادس. يمكننا على كل الأحوال وضع ملاحظات عامة حول المعايير التصميمية للتابع f. بعد ذلك، سندرس بشكل خاص تصميم الصناديق S.

المعايير التصميمية للتابع f

يقدم التابع F عنصر البعثرة في نظام تشفير فيستيل، أي يجب أن يكون من الصعب إعادة بناء التبديل المنجز من خلال F. إحدى المعايير الواضحة أن يكون التابع F غير خطي، كما ناقشنا ذلك سابقا. هناك عدة مقاييس لعدم الخطية ولكنها تخرج عن نطاق بحث هذا المرجع. نستطيع القول بخطوط عريضة أنه كلما كان الحصول على قيمة تقريبية للتابع F من خلال مجموعة معادلات خطية أصعب، كلما كانت لا خطية التابع f أقوى.

يجب الأخذ بعين الاعتبار معايير أخرى عند تصميم التابع f. نرغب بأن يكون للخوارزمية خاصية تراكمية جيدة. لنتذكر بشكل عام أن هذا يعني ما يلي: تغيير خانة دخل واحدة تؤدي إلى تغيير عدة خانات خرج. النسخة الأكثر تشددا من هذا هو مايدعى المعيار التراكمي (أو الانهياري) الدقيق (SAC-Strict Avalanch Ctrterion) ، والتي تقول أن أية خانة خرج j من الصندوق S يجب أن تتغير باحتمال مقداره ½ عندما يتم عكس حالة أية خانة دخل مفردة، وذلك من أجل قيم I,j. ومع أن المعيار SAC مخصص للصناديق S، إلا أنه يمكن تطبيق نفس المعيار على كل F ككل. يعتبر هذا الموضوع هاما بشكل خاص عند الحديث عن تصميمات لا تحوي صناديق S.

هناك معيار آخر وهو معيار استقلالية الخانة (BIC-Bit Independence Criterion)، والتي تقوم بأنه يجب أن تتغير خانات الخرج k,j بشكل مستقل عن بعضها عندما تنعكس أية خانة دخل مفردة i، وذلك من أجل جميع قيم k,j,i. يعمل المعياران BIC, SAC على تقوية فعالية تابع البعثرة.

تصميم صندوق S

يعتبر تصميم صندوق S من المواضيع الأكثر تطرقا للبحث في حقل التشفير الكتلي المتناظر فالنشرات التي تطرح هذا الموضع أكثر من أن تعد. سنذكر هنا بعض المبادئ العامة.

نريد في الجوهر أن ينعكس أي تغيير في شعاع الدخل للصندوق S على شكل تغير عشوائي في الخرج. يجب أن تكون علاقة الخرج بالدخل غير خطية وأن يكون من الصعب التقريب إليها عن طريق معادلات خطية.

يعتبر الحجم من المميزات الواضحة لصندوق S. يملك صندوق S ذو الأبعاد m x m دخلا مكونا من m خانة. أبعاد صناديق S الخاصة بخوارزمية DES هي 6 x 4، بينما صناديق S الخاصة بخوارزمية Blowfish، والتي سيتم شرحها لاحقا، تمتلك الأبعاد 8 x 32.

انظر أيضاً

الهامش

  1. ^ "FR Doc 04-16894". Edocket.access.gpo.gov. Retrieved 2009-06-02.
  2. ^ S. Kumar, C. Paar, J. Pelzl, G. Pfeiffer, A. Rupp, M. Schimmler, "How to Break DES for Euro 8,980". 2nd Workshop on Special-purpose Hardware for Attacking Cryptographic Systems — SHARCS 2006, Cologne, Germany, April 3–4, 2006.

المراجع

وصلات خارجية

الكلمات الدالة:
تمّ الاسترجاع من "https://www.marefa.org/w/index.php?title=معيار_تشفير_المعطيات&oldid=1164171"