بازدياد درجة عديدة حدود تيلور، فإنها تقترب من الدالة الصحيحة. هذا الرسم يُظهر
sin
x
{\displaystyle \sin x}
(بالأسود) وتقريب تيلور، وعديدات الحدود بدرجات
1 ,
3 ,
5 ,
7 ,
9 ,
11 and
13 .
دالة أسية (بالأزرق)، ومجموع أول
n +1 حد من متسلسلة تيلور لها عند 0 (بالأحمر).
متسلسلة تيلور أو مجموع تايلور Taylor series هو عبارة عن متسلسلة تمكن المرء من كتابة دالة رياضية في شكل متسلسلة.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
متسلسلة تايلور المنتهية إذا إعتبرنا الدالة الرياضية (f(x قابلة للإشتقاق n مرة في النقطة
x
0
{\displaystyle {x}_{0}\!}
f
(
x
)
=
T
n
(
x
)
+
R
n
(
x
)
{\displaystyle f(x)=T_{n}(x)+R_{n}(x)\!}
T
n
(
x
)
{\displaystyle T_{n}(x)\!}
T
n
(
x
)
=
∑
k
=
0
n
f
k
(
x
0
)
k
!
(
x
−
x
0
)
k
{\displaystyle T_{n}(x)=\sum _{k=0}^{n}{\frac {f^{k}(x_{0})}{k!}}(x-x_{0})^{k}}
T
n
(
x
)
{\displaystyle T_{n}(x)}
للدالة f في النقطة
x
0
{\displaystyle x_{0}}
متسلسلة تايلور اللامنتهية إذا أخذنا المتسلسلة المنتهية لتايلور و عوضنا n بلانهاية فإننا نحصل على متسلسلة لا منتهية هي بذاتها الدالة f أي أن الجزء
R
n
(
x
)
{\displaystyle R_{n}(x)\!}
تطبيقات متسلسلة تايلور لمتسلسلة تايلور عدة منافع لعل أهمها أنها تسمح بالتعبير عن أي دالة رياضية عن طريق متعدد حدود فيمكننا ذلك من إيجاد حلول تقريبية لمسألة ما إذا كان الحل الدقيق مستعصيا. كما تكتسي متسلسلة تايلور أهمية كبرى في الرياضيات الرقمية حيث تقوم العديد من الخوارزميات المعتمدة لحل المعادلات هناك على متسلسلة تايلور. يجدر بالإشارة أن كل التطبيقات العملية هي تطبيقات للمتسلسلة المنتهية مما يحتم أن نأخذ بعين الإعتبار الدقة التي نريد أن نصل إليها في حلنا لمعادلة ما. ففي حين أن نظام هبوط الطائرات الآلي يتحمل خطئا بين متر أو مترين في موقع الهبوط فإن موضع الرأس الذي يقرؤ المعطيات من إسطوانة لا يقبل إلا خطأ في حدود جزء من المليون من المتر.
مبرهنة تايلور في التحليل الرياضي ، تعطي مبرهنة تايلور تقريبا لتابع قابل للمفاضلة قرب نقطة ما عن طريق كثير حدود معاملاته تعتمد على مشتقات التابع في تلك النقطة .
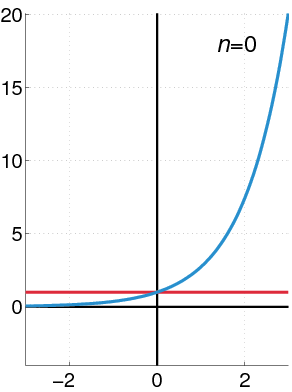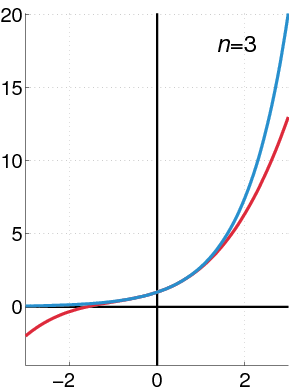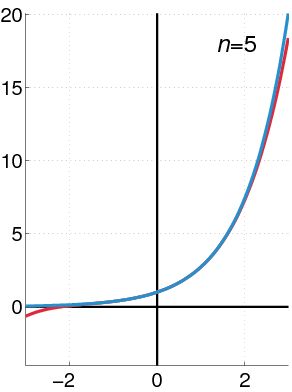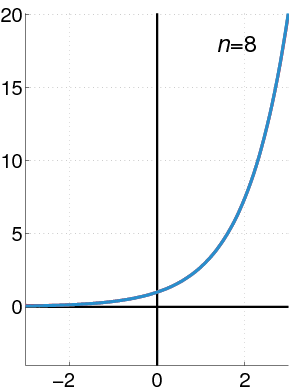
المثال الأكثر بساطة هو الدالة الأسية قرب النقطة صفر :
e
x
≈
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
+
x
N
N
!
.
{\displaystyle {\textrm {e}}^{x}\approx 1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots +{\frac {x^{N}}{N!}}.}
متسلسلة تيلور متعددة المتغيرات The Taylor series may also be generalized to functions of more than one variable with
T
(
x
1
,
…
,
x
d
)
=
{\displaystyle T(x_{1},\dots ,x_{d})=}
=
∑
n
1
=
0
∞
⋯
∑
n
d
=
0
∞
(
x
1
−
a
1
)
n
1
⋯
(
x
d
−
a
d
)
n
d
n
1
!
⋯
n
d
!
(
∂
n
1
+
⋯
+
n
d
f
∂
x
1
n
1
⋯
∂
x
d
n
d
)
(
a
1
,
…
,
a
d
)
.
{\displaystyle =\sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{d}=0}^{\infty }{\frac {(x_{1}-a_{1})^{n_{1}}\cdots (x_{d}-a_{d})^{n_{d}}}{n_{1}!\cdots n_{d}!}}\,\left({\frac {\partial ^{n_{1}+\cdots +n_{d}}f}{\partial x_{1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}\right)(a_{1},\dots ,a_{d}).\!}
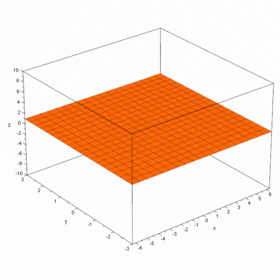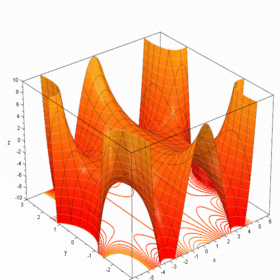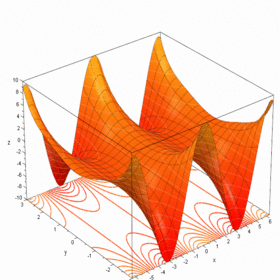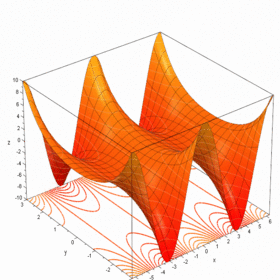
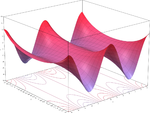
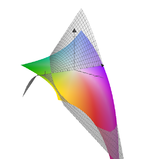
مثال Second-order Taylor series approximation (in gray) of a function
f
(
x
,
y
)
=
e
x
log
(
1
+
y
)
{\displaystyle f(x,y)=e^{x}\log {(1+y)}}
around origin.
Compute a second-order Taylor series expansion around point
(
a
,
b
)
=
(
0
,
0
)
{\displaystyle (a,b)=(0,0)}
f
(
x
,
y
)
=
e
x
log
(
1
+
y
)
.
{\displaystyle f(x,y)=e^{x}\log(1+y).\,}
Firstly, we compute all partial derivatives we need
f
x
(
a
,
b
)
=
e
x
log
(
1
+
y
)
|
(
x
,
y
)
=
(
0
,
0
)
=
0
,
{\displaystyle f_{x}(a,b)=e^{x}\log(1+y){\bigg |}_{(x,y)=(0,0)}=0\,,}
f
y
(
a
,
b
)
=
e
x
1
+
y
|
(
x
,
y
)
=
(
0
,
0
)
=
1
,
{\displaystyle f_{y}(a,b)={\frac {e^{x}}{1+y}}{\bigg |}_{(x,y)=(0,0)}=1\,,}
f
x
x
(
a
,
b
)
=
e
x
log
(
1
+
y
)
|
(
x
,
y
)
=
(
0
,
0
)
=
0
,
{\displaystyle f_{xx}(a,b)=e^{x}\log(1+y){\bigg |}_{(x,y)=(0,0)}=0\,,}
f
y
y
(
a
,
b
)
=
−
e
x
(
1
+
y
)
2
|
(
x
,
y
)
=
(
0
,
0
)
=
−
1
,
{\displaystyle f_{yy}(a,b)=-{\frac {e^{x}}{(1+y)^{2}}}{\bigg |}_{(x,y)=(0,0)}=-1\,,}
f
x
y
(
a
,
b
)
=
f
y
x
(
a
,
b
)
=
e
x
1
+
y
|
(
x
,
y
)
=
(
0
,
0
)
=
1.
{\displaystyle f_{xy}(a,b)=f_{yx}(a,b)={\frac {e^{x}}{1+y}}{\bigg |}_{(x,y)=(0,0)}=1.}
The Taylor series is
T
(
x
,
y
)
=
f
(
a
,
b
)
+
(
x
−
a
)
f
x
(
a
,
b
)
+
(
y
−
b
)
f
y
(
a
,
b
)
+
1
2
!
[
(
x
−
a
)
2
f
x
x
(
a
,
b
)
+
2
(
x
−
a
)
(
y
−
b
)
f
x
y
(
a
,
b
)
+
(
y
−
b
)
2
f
y
y
(
a
,
b
)
]
+
⋯
,
{\displaystyle {\begin{aligned}T(x,y)=f(a,b)&+(x-a)\,f_{x}(a,b)+(y-b)\,f_{y}(a,b)\\&+{\frac {1}{2!}}\left[(x-a)^{2}\,f_{xx}(a,b)+2(x-a)(y-b)\,f_{xy}(a,b)+(y-b)^{2}\,f_{yy}(a,b)\right]+\cdots \,,\end{aligned}}}
which in this case becomes
T
(
x
,
y
)
=
0
+
0
(
x
−
0
)
+
1
(
y
−
0
)
+
1
2
[
0
(
x
−
0
)
2
+
2
(
x
−
0
)
(
y
−
0
)
+
(
−
1
)
(
y
−
0
)
2
]
+
⋯
=
y
+
x
y
−
y
2
2
+
⋯
.
{\displaystyle {\begin{aligned}T(x,y)&=0+0(x-0)+1(y-0)+{\frac {1}{2}}{\Big [}0(x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{\Big ]}+\cdots \\&=y+xy-{\frac {y^{2}}{2}}+\cdots .\end{aligned}}}
Since log(1 + y ) is analytic in |y | < 1, we have
e
x
log
(
1
+
y
)
=
y
+
x
y
−
y
2
2
+
⋯
{\displaystyle e^{x}\log(1+y)=y+xy-{\frac {y^{2}}{2}}+\cdots }
for |y | < 1.
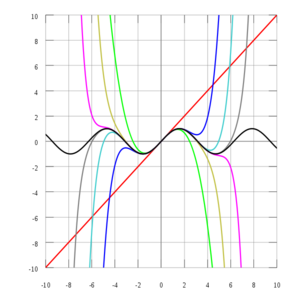
قائمة متسلسلات مكلورين لبعض الدوال الشائعة انظر أيضاً قائمة المتسلسلات الرياضية An 8th degree approximation of the cosine function in the
complex plane .
The two above curves put together.
An animation of the approximation.
Several important Maclaurin series expansions follow.[1] x .
دالة أسية :
e
x
=
∑
n
=
0
∞
x
n
n
!
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
for all
x
{\displaystyle \mathrm {e} ^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots {\text{ for all }}x\!}
لوغاريتم طبيعي :
log
(
1
−
x
)
=
−
∑
n
=
1
∞
x
n
n
for
−
1
≤
x
<
1
{\displaystyle \log(1-x)=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}{\text{ for }}-1\leq x<1}
log
(
1
+
x
)
=
∑
n
=
1
∞
(
−
1
)
n
+
1
x
n
n
for
−
1
<
x
≤
1
{\displaystyle \log(1+x)=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n}}{\text{ for }}-1<x\leq 1}
متسلسلة هندسية محدودة:
1
−
x
m
+
1
1
−
x
=
∑
n
=
0
m
x
n
for
x
≠
1
and
m
∈
N
0
{\displaystyle {\frac {1-x^{m+1}}{1-x}}=\sum _{n=0}^{m}x^{n}\quad {\mbox{ for }}x\not =1{\text{ and }}m\in \mathbb {N} _{0}\!}
متسلسلة هندسية غير محدودة:
1
1
−
x
=
∑
n
=
0
∞
x
n
for
|
x
|
<
1
{\displaystyle {\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}{\text{ for }}|x|<1\!}
Variants of the infinite geometric series:
x
m
1
−
x
=
∑
n
=
m
∞
x
n
for
|
x
|
<
1
and
m
∈
N
0
{\displaystyle {\frac {x^{m}}{1-x}}=\sum _{n=m}^{\infty }x^{n}\quad {\mbox{ for }}|x|<1{\text{ and }}m\in \mathbb {N} _{0}\!}
x
(
1
−
x
)
2
=
∑
n
=
1
∞
n
x
n
for
|
x
|
<
1
{\displaystyle {\frac {x}{(1-x)^{2}}}=\sum _{n=1}^{\infty }nx^{n}\quad {\text{ for }}|x|<1\!}
1
(
1
−
x
)
2
=
∑
n
=
1
∞
n
x
n
−
1
for
|
x
|
<
1
{\displaystyle {\frac {1}{(1-x)^{2}}}=\sum _{n=1}^{\infty }nx^{n-1}\quad {\text{ for }}|x|<1\!}
الجذر التربيعي :
1
+
x
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
(
1
−
2
n
)
(
n
!
)
2
(
4
n
)
x
n
=
1
+
1
2
x
−
1
8
x
2
+
1
16
x
3
−
5
128
x
4
+
…
for
−
1
<
x
≤
1
{\displaystyle {\sqrt {1+x}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}=1+\textstyle {\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+\dots {\text{ for }}-1<x\leq 1}
Binomial series (includes the square root for α = 1/2 and the infinite geometric series for α = −1):
(
1
+
x
)
α
=
∑
n
=
0
∞
(
α
n
)
x
n
for all
|
x
|
<
1
and all complex
α
{\displaystyle (1+x)^{\alpha }=\sum _{n=0}^{\infty }{\alpha \choose n}x^{n}\quad {\mbox{ for all }}|x|<1{\text{ and all complex }}\alpha \!}
with generalized binomial coefficients
(
α
n
)
=
∏
k
=
1
n
α
−
k
+
1
k
=
α
(
α
−
1
)
⋯
(
α
−
n
+
1
)
n
!
{\displaystyle {\alpha \choose n}=\prod _{k=1}^{n}{\frac {\alpha -k+1}{k}}={\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}}
Trigonometric functions :
sin
x
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
!
x
2
n
+
1
=
x
−
x
3
3
!
+
x
5
5
!
−
⋯
for all
x
{\displaystyle \sin x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots {\text{ for all }}x\!}
cos
x
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
x
2
n
=
1
−
x
2
2
!
+
x
4
4
!
−
⋯
for all
x
{\displaystyle \cos x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots {\text{ for all }}x\!}
tan
x
=
∑
n
=
1
∞
B
2
n
(
−
4
)
n
(
1
−
4
n
)
(
2
n
)
!
x
2
n
−
1
=
x
+
x
3
3
+
2
x
5
15
+
⋯
for
|
x
|
<
π
2
{\displaystyle \tan x=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1}=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots {\text{ for }}|x|<{\frac {\pi }{2}}\!}
حيث Bs هي أرقام برنولي .
sec
x
=
∑
n
=
0
∞
(
−
1
)
n
E
2
n
(
2
n
)
!
x
2
n
for
|
x
|
<
π
2
{\displaystyle \sec x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}{\text{ for }}|x|<{\frac {\pi }{2}}\!}
arcsin
x
=
∑
n
=
0
∞
(
2
n
)
!
4
n
(
n
!
)
2
(
2
n
+
1
)
x
2
n
+
1
for
|
x
|
≤
1
{\displaystyle \arcsin x=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}{\text{ for }}|x|\leq 1\!}
arccos
x
=
π
2
−
arcsin
x
=
π
2
−
∑
n
=
0
∞
(
2
n
)
!
4
n
(
n
!
)
2
(
2
n
+
1
)
x
2
n
+
1
for
|
x
|
≤
1
{\displaystyle \arccos x={\pi \over 2}-\arcsin x={\pi \over 2}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}{\text{ for }}|x|\leq 1\!}
arctan
x
=
∑
n
=
0
∞
(
−
1
)
n
2
n
+
1
x
2
n
+
1
for
|
x
|
≤
1
{\displaystyle \arctan x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}{\text{ for }}|x|\leq 1\!}
Hyperbolic functions :
sinh
x
=
∑
n
=
0
∞
x
2
n
+
1
(
2
n
+
1
)
!
=
x
+
x
3
3
!
+
x
5
5
!
+
⋯
for all
x
{\displaystyle \sinh x=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots {\text{ for all }}x\!}
cosh
x
=
∑
n
=
0
∞
x
2
n
(
2
n
)
!
=
1
+
x
2
2
!
+
x
4
4
!
+
⋯
for all
x
{\displaystyle \cosh x=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+\cdots {\text{ for all }}x\!}
tanh
x
=
∑
n
=
1
∞
B
2
n
4
n
(
4
n
−
1
)
(
2
n
)
!
x
2
n
−
1
=
x
−
1
3
x
3
+
2
15
x
5
−
17
315
x
7
+
⋯
for
|
x
|
<
π
2
{\displaystyle \tanh x=\sum _{n=1}^{\infty }{\frac {B_{2n}4^{n}(4^{n}-1)}{(2n)!}}x^{2n-1}=x-{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}-{\frac {17}{315}}x^{7}+\cdots {\text{ for }}|x|<{\frac {\pi }{2}}\!}
a
r
s
i
n
h
(
x
)
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
4
n
(
n
!
)
2
(
2
n
+
1
)
x
2
n
+
1
for
|
x
|
≤
1
{\displaystyle \mathrm {arsinh} (x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}{\text{ for }}|x|\leq 1\!}
a
r
t
a
n
h
(
x
)
=
∑
n
=
0
∞
x
2
n
+
1
2
n
+
1
for
|
x
|
<
1
{\displaystyle \mathrm {artanh} (x)=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}{\text{ for }}|x|<1\!}
Lambert's W function :
W
0
(
x
)
=
∑
n
=
1
∞
(
−
n
)
n
−
1
n
!
x
n
for
|
x
|
<
1
e
{\displaystyle W_{0}(x)=\sum _{n=1}^{\infty }{\frac {(-n)^{n-1}}{n!}}x^{n}{\text{ for }}|x|<{\frac {1}{\mathrm {e} }}\!}
The numbers B k summation expansions of tan(x ) and tanh(x ) are the Bernoulli numbers . The E k x ) are Euler numbers .
انظر أيضاً الهامش المصادر Abramowitz, Milton ; Stegun, Irene A. (1970), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables Dover Publications , Ninth printing Thomas, George B. Jr.; Finney, Ross L. (1996), Calculus and Analytic Geometry (9th ed.) , Addison Wesley, ISBN 0-201-53174-7 Greenberg, Michael (1998), Advanced Engineering Mathematics (2nd ed.) , Prentice Hall, ISBN 0-13-321431-1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
وصلات خارجية



















![{\displaystyle {\begin{aligned}T(x,y)=f(a,b)&+(x-a)\,f_{x}(a,b)+(y-b)\,f_{y}(a,b)\\&+{\frac {1}{2!}}\left[(x-a)^{2}\,f_{xx}(a,b)+2(x-a)(y-b)\,f_{xy}(a,b)+(y-b)^{2}\,f_{yy}(a,b)\right]+\cdots \,,\end{aligned}}}](https://www.marefa.org/api/rest_v1/media/math/render/svg/83637bd427241854df42cc15345d6683b3e09887)
![{\displaystyle {\begin{aligned}T(x,y)&=0+0(x-0)+1(y-0)+{\frac {1}{2}}{\Big [}0(x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{\Big ]}+\cdots \\&=y+xy-{\frac {y^{2}}{2}}+\cdots .\end{aligned}}}](https://www.marefa.org/api/rest_v1/media/math/render/svg/620c279c9d7f3f4c1fca3546c7cb3e5ee3b31f53)