متراجحة يونگ لحواصل الضرب

متراجحة يونگ Young inequality مبرهنة رياضية تقول مايلي:

• $a^{T}b\leq \alpha a^{T}a+{\frac {1}{\alpha }}b^{T}b$

حيث a و b مصفوفتان و $\alpha$ عدد طبيعي أكبر من صفر.
لهذه المتراجحة تطبيقات عديدة في البراهين الرياضياتية وفي نظرية التحكم القوي.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التعميم المصفوفي

T. Ando proved a generalization of Young's inequality for complex matrices ordered by Loewner ordering. It states that for any pair A, B of complex matrices of order n there exists a unitary matrix U such that

$U^{*}|AB^{*}|U\preceq {\frac {1}{p}}|A|^{p}+{\frac {1}{q}}|B|^{q},$

where * denotes the conjugate transpose of the matrix and $|A|={\sqrt {A^{*}A}}$.

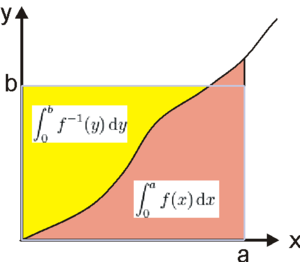
 النسخة القياسية للدوال المتزايدة

مساحة المستطيل a,b لا يمكن أن تكون أكبر من مجموع المساحات تحت الدوال $F$ (أحمر) و $F^{-1}$ (أصفر)

For the standard version of the inequality, let f denote a real-valued, continuous and strictly increasing function on [0, c] with c > 0 and f(0) = 0. Let f⁻¹ denote the inverse function of f. Then, for all a ∈ [0, c] and b ∈ [0, f(c)],

$ab\leq \int _{0}^{a}f(x)\,dx+\int _{0}^{b}f^{-1}(x)\,dx$

with equality if and only if b = f(a).

With $f(x)=x^{p-1}$ and $f^{-1}(y)=y^{q-1}$, this reduces to standard version for conjugate Hölder exponents.

For details and generalizations we refer to the paper of Mitroi & Niculescu.

 التعميم باستخدام تحويلات فنشل-لجاندر

إذا كانت f هي convex function و تحويل لجاندر لها (convex conjugate) مميز بالحرف g، إذن،

$ab\leq f(a)+g(b).$

This follows immediately from the definition of the Legendre transform.

More generally, if f is a convex function defined on a real vector space $X$ and its convex conjugate is denoted by $f^{\star }$ (and is defined on the dual space $X^{\star }$), then

$\langle u,v\rangle \leq f^{\star }(u)+f(v).$

where $\langle \cdot ,\cdot \rangle :X^{\star }\times X\to \mathbb {R}$ is the dual pairing.

 أمثلة

• The Legendre transform of f(a) = a^p/p is g(b) = b^q/q with q such that 1/p + 1/q = 1, and thus Young's inequality for conjugate Hölder exponents mentioned above is a special case.
• The Legendre transform of f(a) = e^a – 1 is g(b) = 1 − b + b ln b, hence ab ≤ e^a − b + b ln b for all non-negative a and b. This estimate is useful in large deviations theory under exponential moment conditions, because b ln b appears in the definition of relative entropy, which is the rate function in Sanov's theorem.

 انظر أيضاً

• Convex conjugate
• Integral of inverse functions
• Legendre transformation

 المراجع

• قالب:Jarchow Locally Convex Spaces

 وصلات خارجية

• Young's Inequality at PlanetMath
• Eric W. Weisstein, Young's Inequality at MathWorld.