متباينة (جبر)

يجب ألا يـُخلـَط بينها وبين تباين (إحصاء).

The feasible regions of linear programming are defined by a set of inequalities.

في الرياضيات، المتباينة أو المتراجحة إنگليزية: Inequality هي علاقة رياضية تعبّر عن اختلاف قيمة عنصرين رياضيين، وغالباً ما تحوي إحدى الرموز (> ، < ، ≥ ، ≤).تعريف الجودة (قاموس الرياضيات المصور) | موقع الويب = www.mathsisfun.com | access-date = 2019-12-03}} </ref> يتم استخدامه في أغلب الأحيان لمقارنة رقمين في سطر الأرقام بحجم. هناك العديد من الرموز المختلفة المستخدمة لتمثيل أنواع مختلفة من عدم المساواة:

• تدوين 'يعني أن' 'a' 'أقل من' b '.
• تدوين "أ" "" "ب" "يعني أن" أ "أكبر من" ب ".

في كلتا الحالتين ، "أ" لا تساوي "ب". تُعرف هذه العلاقات باسم عدم المساواة الصارمة '، بمعنى أن "a" أقل تمامًا من (resp. ، أكبر تمامًا من)' 'b.

على عكس التفاوتات الصارمة ، هناك نوعان من علاقات عدم المساواة التي ليست صارمة:

• تدوين "أ" "أ" "ب" أو "أ" أ "" أ "يعني أن" أ "أقل من أو يساوي" ب "(أو ، على قدم المساواة ، في معظم "ب" ، أو ليس أكبر من "ب" ").
• تدوين "أ" "أ" "ب" أو "أ" أ "" أ "يعني أن" أ "أكبر من أو يساوي" ب "(أو ، على قدم المساواة ، في الأقل "ب" ، أو ليس أقل من "ب" ").

(يمكن أيضًا تمثيل العلاقة "ليست أكبر من" بعلامة "أ" "أ" "ب" ، رمز "أكبر من" مائل بقطعة مائلة ، "لا". وينطبق الشيء نفسه على "ليس أقل من "و" "a" "≮" "b".)

إذا كانت القيم المعنية هي عناصر مجموعة مرتبة ، مثل عدد صحيح أو رقم حقيقي ، فيمكن مقارنتها في الحجم. من ناحية أخرى ، فإن التدوين "أ" "أ" "ب" يعني أن "أ" لا تساوي "ب" ، وفي بعض الأحيان يعتبر شكلاً من أشكال عدم المساواة الصارمة.لا يقول أن أحدهما أكبر من الآخر ، أو حتى أنه يمكن مقارنتهما في الحجم في العلوم الهندسية ، يتمثل الاستخدام الأقل رسمية للتدوين في الإشارة إلى أن كمية ما "أكبر بكثير" من الأخرى ، عادةً بواسطة عدة أوامر الحجم. هذا يعني أنه يمكن إهمال القيمة الأقل بتأثير ضئيل على دقة تقريب (مثل حالة الحد فائق اللونية في الفيزياء).

• تدوين "أ" "أ" "ب" يعني أن "أ" أقل بكثير من "ب". (في نظرية القياس ، ومع ذلك ، يتم استخدام هذا الترميز لـ الاستمرارية المطلقة ، وهو مفهوم غير ذي صلة.)
• تدوين "أ" "أ" "ب" يعني أن "أ" أكبر بكثير من "ب".)

في جميع الحالات المذكورة أعلاه ، أي رمزان يعكسان بعضهما البعض متماثلان ؛ b 'و' 'b' 'متكافئان ، إلخ.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الخصائص على سطر الرقم

يحكم عدم المساواة ما يلي خصائص. جميع هذه الخصائص معلقة أيضًا إذا تم استبدال جميع أوجه عدم المساواة غير الصارمة (≤ و ≥) بأوجه عدم المساواة الصارمة المقابلة لها (<و>) - وفي حالة تطبيق وظيفة - تقتصر وظائف الرتابة على "بدقة" 'وظيفة رتابة.

 الحديث

العلاقات ≤ و ≥ هما العكس ، وهذا يعني أنه بالنسبة لأي رقم حقيقي 's' 'a' 'و' 'b' ':

'≤' 'b' 'و' 'b' 'متساويان.

 عبورية

تنص الخاصية متعدية عدم المساواة على أنه بالنسبة لأي رقم حقيقي "أ" و "ب" و "ج":

إذا و '، ثم' .

إذا كان "أي من" المبنى يمثل عدم مساواة صارمة ، فإن الاستنتاج هو عدم مساواة صارمة:

إذا و '، ثم' .

إذا "أ" و ب ، ثم أ .

 الجمع والطرح

If x < y, then x + a < y + a.

الثابت المشترك c قد يكون المضافة إلى أو طرح من كلا الجانبين من عدم المساواة. لذلك ، لأي رقم حقيقي a ، 'b' '،' c :

إذا '≤' ، ثم '+' '+' c و 'a' '-' 'c' ≤ b - c .

بمعنى آخر ، يتم الحفاظ على علاقة عدم المساواة ضمن الإضافة (أو الطرح) والأرقام الحقيقية هي مجموعة مرتبة قيد الإضافة.

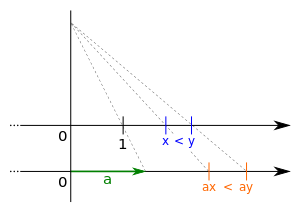
 الضرب والقسمة

If x < y and a > 0, then ax < ay.

If x < y and a < 0, then ax > ay.

تشير الخصائص التي تتعامل مع الضرب والقسمة) إلى أنه بالنسبة لأي أرقام حقيقية ، "أ" و "ب" و غير صفري "ج":

إذا 0 b و c > 0 ، ثم ac ≤ bc و '/' 'c' '≤' 'ب / ج .

إذا "أ" ≤ b و c <0 ، ثم ac ≥ bc و 'a' '/' 'c' '≥' 'ب / ج .

بمعنى آخر ، يتم الحفاظ على علاقة عدم المساواة في ظل الضرب والقسمة مع ثابت إيجابي ، ولكن يتم عكس عندما يتعلق الأمر ثابت ثابت. بشكل عام ، ينطبق هذا على حقل مرتب. لمزيد من المعلومات ، راجع "" § الحقول المطلوبة ".

 معكوس المضاف

تنص خاصية معكوس المضاف على أنه بالنسبة لأي أرقام حقيقية "أ" و "ب":

إذا "أ" "أ" "ب" ، ثم - "أ" "أ" - "ب".

 معكوس المضاعفة

إذا كان كلا الرقمين موجبًا ، فعندئذٍ تكون علاقة عدم المساواة بين معكوس المضاعف عكس العلاقة بين الأرقام الأصلية. وبشكل أكثر تحديدًا ، لأي أرقام حقيقية غير صفرية "أ" و "ب" "كلاهما إيجابي (أو كلاهما سلبي):

إذا "أ" ≤ '، ثم 1 /' 'أ' '≥ 1 /' 'ب' '.

يمكن أيضًا كتابة جميع الحالات المتعلقة بعلامات "a" و "b" في chained notation ، على النحو التالي:

إذا كانت 0 < a ≤ b ، ثم 1 / a ≥ 1 / b > 0.

إذا "أ" '≤' 'ب' '<0 ، ثم 0> 1 /' 'أ' '≥ 1 /' 'ب' '.

إذا "أ" '<0 <' 'ب "" ، فثم 1 /' 'أ' '<0 <1 /' 'ب' '.

 تطبيق وظيفة لكلا الجانبين

The graph of y = ln x

أي رتابة حليف متزايد وظيفة ، من خلال تعريفه ,يمكن تطبيقه على كلا الجانبين من عدم المساواة دون كسر علاقة عدم المساواة (شريطة أن يكون كلا التعبرين في مجال من هذه الوظيفة). ومع ذلك ، فإن تطبيق وظيفة تناقص رتابة على جانبي اللامساواة يعني أن علاقة عدم المساواة ستنعكس. تعد كل من قواعد معكوس المضاف ، وعكسة المضاعف للأعداد الموجبة ، مثالين على تطبيق دالة تناقص رتابة.

إذا كان عدم المساواة صارمًا ( و 'و' 'الوظيفة رتابة تمامًا ، فإن عدم المساواة يبقى صارمًا. إذا كان هناك واحد فقط من هذه الشروط صارم ، فإن عدم المساواة الناتج يكون غير صارم. في الواقع ، تعد كل من القواعد المقلوبة المضافة والمتعددة أمثلة على تطبيق دالة تناقص رتابة "صارمة".

بعض الأمثلة على هذه القاعدة هي:

• رفع كلا الجانبين من عدم المساواة إلى قوة n > 0 (equiv. ، - n <0) ، عندما تكون a و b أرقام حقيقية إيجابية:

0 ≤ a ≤ b ⇔ 0 ≤ a ⁿ ≤ b ⁿ .

0 ≤ a ≤ b ⇔ ^{- n} ≥ b ^{- n </ سوب> ≥ 0.}

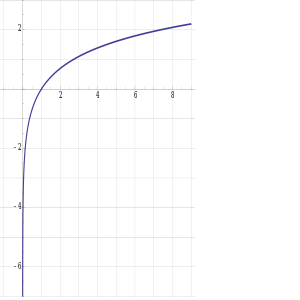
• أخذ اللوغاريتم الطبيعي على جانبي اللامساواة ، عندما تكون "أ" و "ب" عبارة عن أرقام حقيقية إيجابية:

0 < a ≤ b ⇔ ln ( a ) ≤ ln ( b ).

0 < a < b ⇔ ln ( a ) <ln ( b ).

(هذا صحيح لأن اللوغاريتم الطبيعي هو وظيفة متزايدة بشكل صارم.)

 التعاريف الرسمية والتعميمات

(غير صارم) 'ترتيب جزئي' هو علاقة ثنائية ≤ على مجموعة P وهي انعكاسية ، المضادة للتماثل ، و متعدية.أي أنه بالنسبة للجميع "أ" و "ب" و "ج" في "ب" ، يجب أن يستوفي الشروط الثلاثة التالية:

1. a ≤ '( الانعكاسية)
2. إذا 'و' '، ثم' 'a' '=' ( عدم التناسق)
3. إذا "أ" 'و' '، ثم' ( العابرة)

تسمى المجموعة ذات الترتيب الجزئي 'مجموعة مرتبة جزئيًا' .تلك هي البديهيات الأساسية التي يجب أن يفي بها كل نوع من النظام. تتضمن البديهيات الأخرى الموجودة لتعريفات أخرى للأوامر على مجموعة "" P "":

1. لكل "أ" و "ب" في "ب" أو "أ" "أ" "أ" أو "أ" "أ" ([[ترتيب كلي] ]).
2. للجميع a و 'b' 'في' 'P' 'والتي' 'a' ، يوجد 'c' 'في' 'P' 'بحيث c (ترتيب كثيف).
3. كل [فارغ (رياضيات) | مجموعة فرعية]] من "P" مع الحد الأعلى له "الحد الأدنى" الحد الأعلى (الأسمى) في P (أقل الحدود العليا ملزمة) .

 الحقول المطلوبة

المقالة الرئيسية: Ordered field

إذا كان ( F ، + ، ×) هو حقل و ≤ هو ترتيب كلي على F ، ثم ( F ، + ، × ، ≤) تسمى "[" حقل مرتبة "" إذا وفقط إذا:

• a ≤ تعني a + c ≤ b + c ؛
• 0 ≤ a و 0 ≤ b تعني 0 ≤ a × b .

كل من ( 'Q' و + و × و ≤) و ( 'R' و + و × و ≤) حقل مرتب ، لكن ≤ لا يمكن تعريفها من أجل إجراء ( 'C' ، + ، × ، ≤) حقل مرتب ،لأن −1 هي مربع "أنا" وبالتالي ستكون إيجابية. بالإضافة إلى كونه حقلًا مرتبًا ، فإن 'R' لديه أيضًا خاصية الحد الأدنى العلوي. في الواقع ، يمكن تعريف 'R' على أنه الحقل المطلوب الوحيد بهذه الجودة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 تدوين بالسلاسل

تدوين 'و' b "" ، والتي ، من خلال خاصية النقل أعلاه ، تتبع أيضًا ذلك "" "" "" "". بموجب القوانين المذكورة أعلاه ، يمكن للمرء إضافة أو طرح نفس الرقم على كل المصطلحات الثلاثة ، أو ضرب أو تقسيم المصطلحات الثلاثة على نفس الرقم غير الصفري وعكس جميع أوجه عدم المساواة إذا كان هذا الرقم سالبًا. وبالتالي ، على سبيل المثال ، مكافئة لـ a 'c' '-' 'e' '.

يمكن تعميم هذا الترميز على أي عدد من المصطلحات: على سبيل المثال ، ₁ ≤ ' ₂ ≤ ... ≤' 'a' '_{' 'n' '}' تعني أن a i ≤ '_{' 'i} +1 لـ i = 1 ، 2 ، ... ، n - 1. بالترانزيت ، هذه الحالة تعادل a _i ≤ '_{' 'j' '} لأي 1' i 'j' '≤' 'n' '.

عند حل أوجه عدم المساواة باستخدام الترميز بالسلاسل ، من الممكن والضروري أحيانًا تقييم المصطلحات بشكل مستقل. على سبيل المثال ، لحل مشكلة عدم المساواة 4 x <2x + 1 '3x' '+ 2 ، لا يمكن عزل' 'x' 'في أي جزء من عدم المساواة من خلال الجمع أو الطرح. بدلاً من ذلك ، يجب حل أوجه عدم المساواة بشكل مستقل ، بحيث تسفر عن "x" و "1/2" و "x" و "x" على التوالي ، والتي يمكن دمجها في الحل النهائي −1 ≤ x <1/2 . في بعض الأحيان ، يتم استخدام الترميز السلاسل مع عدم المساواة في اتجاهات مختلفة ، وفي هذه الحالة يكون المعنى هو الاقتران المنطقي من عدم المساواة بين المصطلحات المجاورة. على سبيل المثال ، a b = c تعني أن a ، 'b' ' "، و" ج "" ≤ "د". يوجد هذا الترميز في بعض لغة البرمجة مثل Python. <! -

 يمثل عدم المساواة على خط الرقم الحقيقي

يمكن تمثيل كل عدم مساواة تتضمن أرقامًا حقيقية على خط الأرقام الحقيقي الذي يعرض المناطق المظلمة على الخط. يتم رسم علامة "<" أو ">" بواسطة دائرة مفتوحة على الرقم. يتم رسم "≤" أو "≥" بدائرة مغلقة أو سوداء.

->

 عدم المساواة الحادة

يقال إن عدم المساواة "حاد" ، إذا لم يكن "مريحًا" ولا يزال صالحًا بشكل عام. بشكل رسمي ، يُطلق على عدم المساواة [[كميا عالميا] φ حاد إذا كان ، بالنسبة لكل عدم مساواة صالحة عالميا '، إذا ' ⇒ φ يحمل ، ثم ψ ⇔ φ يحمل أيضًا. على سبيل المثال ، عدم المساواة ∀ a ∈ ℝ. a ² ≥ 0 حاد ، في حين أن عدم المساواة ∀a ∈ ℝ. a ² ≥ −1 ليست حادة.

 عدم المساواة بين الوسائل

انظر أيضاً: عدم المساواة في الوسائل الحسابية والهندسية

هناك العديد من أوجه عدم المساواة بين الوسائل. على سبيل المثال ، بالنسبة لأي أرقام موجبة "أ" ₁ ، "أ" " ₂ ، ... ،" "a" "_{" "n" "} لدينا H ≤ G ≤ A ≤ Q ، حيث

-

$H=\ frac{n}{1/a_{1}+1/a_{2}+\ cdots+1/a_{n}}$

(الوسط التوافقي)،

-

$G=\ sqrt[n]{a_{1}\ cdota_{2}\ cdotsa_{n}}$

(الوسط الهندسي) ،

-

$A=\ frac{a_{1}+a_{2}+\ cdots+a_{n}}{n}$

(المتوسط الحسابي)،

-

$Q=\ sqrt{\ frac{a_{1}^{2}+a_{2}^{2}+\ cdots+a_{n}^{2}}{n}}$

( التربيعي).

 عدم المساواة في كوشي - شوارز

انظر أيضاً: Cauchy–Schwarz inequality

ينص عدم المساواة بين كوشي وشوارز على أنه بالنسبة لجميع المتجهات "u" و "v" في مساحة المنتج الداخلية ، صحيح أن

خطأ رياضيات (خطأ في الصيغة): {\displaystyle | \ langle \ mathbf {u} ، \ mathbf {v} \ rangle | ^ 2 \ leq \ langle \ mathbf {u} ، \ mathbf {u} \ rangle \ cdot \ langle \ mathbf {v} ، \ mathbf {v} \ rangle ، }

حيث خطأ رياضيات (خطأ في الصيغة): {\displaystyle \ langle \ cdot ، \ cdot \ rangle } هو المنتج الداخلي. تشمل الأمثلة على المنتجات الداخلية المنتج الحقيقي والمعقد نقطة المنتج ؛ في المساحة الإقليدية R ⁿ مع المنتج الداخلي القياسي ، فإن عدم المساواة في Cauchy-Schwarz هو

$\ left(\ sum_{i=1}^{n}u_{i}v_{i}\ right)^{2}\ leq\ left(\ sum_{i=1}^{n}u_{i}^{2}\ right)\ left(\ sum_{i=1}^{n}v_{i}^{2}\ right)$

 عدم المساواة في السلطة

"عدم المساواة في القوة" "" "عبارة عن عدم مساواة تحتوي على مصطلحات من النموذج" 'a' '^{' 'b' '} ، حيث' 'a' 'و' 'b' ' أرقام إيجابية حقيقية أو تعبيرات متغيرة. غالبًا ما تظهر في التمارين [[أولمبياد الرياضيات].

 أمثلة

• لأي 'x' حقيقي ،

$e^{x}\ ge1+x.$

• إذا كان x > 0 و p > 0 ، إذن

$(x^{p}-1)/p\ ge\ ln(x)\ ge(1-{1}/{x^{p}})/p.$

في حدود p → 0 ، تلتقي الحدود العليا والسفلى مع ln ( x ).

• إذا كان x > 0 ، إذن

$x^{x}\ ge\ left(\ frac{1}{e}\ right)^{1/e}.$

• إذا كان x ≥ 1 ، إذن

$x^{x^{x}}\ gex.$

• إذا كانت x ، 'y' '،' 'z' '> 0 ، إذن

$(x+y)^{z}+(x+z)^{y}+(y+z)^{x}>2.$

• لأي أرقام مميزة حقيقية "أ" و "ب" ،

$\ frac{e^{b}-e^{a}}{b-a}>e^{(a+b)/2}.$

• إذا كانت x ، 'y' '> 0 و 0 <' 'p' '<1 ، إذن

$x^{p}+y^{p}>(x+y)^{p}.$

• إذا كانت x ، 'y' '،' 'z' '> 0 ، إذن

$x^{x}y^{y}z^{z}\ ge(xyz)^{(x+y+z)/3}.$

• إذا كان أ ، 'ب' '> 0 ، إذن

$a^{a}+b^{b}\ gea^{b}+b^{a}.$

تم حل هذا التباين من قبل I.Ilani في JSTOR، AMM، Vol.97، No.1، 1990.

• إذا كان أ ، 'ب' '> 0 ، إذن

$a^{ea}+b^{eb}\ gea^{eb}+b^{ea}.$

تم حل هذا التباين بواسطة S.Manyama في AJMAA ، المجلد 7 ، العدد 2 ، العدد 1.100 وبواسطة V.Cirtoaje في JNSA ، المجلد 4 ، الإصدار 2 ، 130-137 ، 2011.

• إذا "أ" ، "ب" ، "ج"> 0 ، إذن

$a^{2a}+b^{2b}+c^{2c}\ gea^{2b}+b^{2c}+c^{2a}.$

• إذا كان أ ، 'ب' '> 0 ، إذن

$a^{b}+b^{a}>1.$

 عدم المساواة المعروفة

انظر أيضاً: List of inequalities

غالبًا ما يستخدم [[عالم الرياضيات] أوجه عدم المساواة في الكميات المربوطة والتي لا يمكن حساب الصيغ الدقيقة لها بسهولة. يتم استخدام بعض أوجه عدم المساواة في كثير من الأحيان بحيث يكون لديهم أسماء:

• عدم المساواة في أزوما
• عدم المساواة في برنولي
• عدم المساواة في بيل
• عدم المساواة في بول
• عدم المساواة بين كوشي وشوارز
• عدم المساواة في تشيبشيف
• عدم المساواة تشيرنوف
• عدم المساواة كريمر راو
• عدم المساواة في هوفينج
• عدم مساواة هولدر
• عدم المساواة في الوسائل الحسابية والهندسية
• عدم المساواة في جنسن
• عدم المساواة في كولموجوروف
• عدم المساواة ماركوف
• عدم المساواة مينكوفسكي
• عدم المساواة في نسبيت
• عدم مساواة بيدو
• عدم المساواة Poincaré
• عدم المساواة في صامويلسون
• عدم المساواة المثلث

 أعداد معقدة وعدم المساواة

مجموعة رقم مركب s $\ mathbb{C}$ مع عملياتها الجمع و الضرب هي حقل ، لكن من المستحيل تحديد أي علاقة ، بحيث يصبح خطأ رياضيات (خطأ في الصيغة): {\displaystyle (\ mathbb {C} ، + ، \ times ، \ le) } [[[حقل مرتب]]]. لجعل خطأ رياضيات (خطأ في الصيغة): {\displaystyle (\ mathbb {C} ، + ، \ times ، \ le) } حقل مرتبة ، يجب أن تفي بالخاصيتين التاليتين:

• إذا '≤' ، ثم '+' 'c' + 'c' '؛
• إذا كان 0 ≤ a و 0 ≤ b ، ثم 0 ≤ a b .

لأن ≤ هو ترتيب كلي ، لأي رقم "" أ "" ، إما 0 "أو" "أو" "" "(في هذه الحالة ، تشير الخاصية الأولى أعلاه إلى أن 0" - " 'أ). في كلتا الحالتين 0 ≤ a ² ؛ هذا يعني أن $i^{2}>0$ و $1^{2}>0$؛ لذلك $-1>0$ و $1>0$ ، مما يعني $(-1+1)>0$ ؛ تناقض. ومع ذلك ، يمكن تعريف العملية so لإرضاء الخاصية الأولى فقط (وهي "إذا" "أ" "أ" "ب" "، ثم" أ "" + "" أ "" " '+' 'c' '"). في بعض الأحيان يستخدم تعريف ترتيب المعجم:

• $a\ leb$ ، إذا $\ mathrm{Re}(a)<\ mathrm{Re}(b)$ أو $\ left(\ mathrm{Re}(a)=\ mathrm{Re}(b)\ right.$ و خطأ رياضيات (خطأ في الصيغة): {\displaystyle \ left. \ mathrm {Im} (a) \ le \ mathrm {Im} (b) \ right). </ الرياضيات> يمكن إثبات ذلك بسهولة لهذا التعريف "a" "≤" "b" "" "a" "+" c "" "" b "" + "c". == عدم المساواة في المتجهات == يمكن أيضًا تعريف علاقات عدم المساواة المماثلة لتلك المحددة أعلاه لـ [[ناقل العمود]]. إذا سمحنا للمتجهات <math> x ، y \ in \ mathbb {R} ^ n } (بمعنى أن خطأ رياضيات (خطأ في الصيغة): {\displaystyle x = (x_1 ، x_2 ، \ ldots ، x_n) ^ \ mathsf {T} </ math> و <math> y = (y_1 و y_2 و \ ldots و y_n) ^ \ mathsf {T} } ، حيث $x_{i}$ و $y_{i}$ أرقام حقيقية بالنسبة إلى خطأ رياضيات (خطأ في الصيغة): {\displaystyle i = 1 ، \ ldots ، n } ) ، يمكننا تحديد العلاقات التالية:
• $x=y$ ، إذا $x_{i}=y_{i}$ لـ خطأ رياضيات (خطأ في الصيغة): {\displaystyle i = 1 ، \ ldots ، n } .
• $x<y$ ، إذا $x_{i}<y_{i}$ لـ خطأ رياضيات (خطأ في الصيغة): {\displaystyle i = 1 ، \ ldots ، n } .
• $x\ leqy$ ، إذا $x_{i}\ leqy_{i}$ لـ خطأ رياضيات (خطأ في الصيغة): {\displaystyle i = 1 ، \ ldots ، n } و خطأ رياضيات (خطأ في الصيغة): {\displaystyle x \ neq y < / الرياضيات>. * <math> x \ leqq y } ، إذا $x_{i}\ leqy_{i}$ لـ خطأ رياضيات (خطأ في الصيغة): {\displaystyle i = 1 ، \ ldots ، n } .

وبالمثل ، يمكننا تحديد العلاقات لـ $x>y$ و $x\ geqy$ و $x\ geqqy$. يتماشى هذا التدوين مع تلك المستخدمة من قبل Matthias Ehrgott في Multicriteria Optimization (انظر المراجع).

الخاصية trichotomy (كما هو مذكور أعلاه) غير صالحة للعلاقات المتجهة. على سبيل المثال ، عندما خطأ رياضيات (خطأ في الصيغة): {\displaystyle x = (2، 5) ^ \ mathsf {T} } و خطأ رياضيات (خطأ في الصيغة): {\displaystyle y = (3، 4) ^ \ mathsf {T} } ، لا يوجد أي صلاحية علاقة عدم المساواة بين هذين المتجهين. أيضًا ، سوف يلزم تعريف معكوس المضاعفة على المتجه قبل دراسة هذه الخاصية. ومع ذلك ، بالنسبة لبقية الخصائص المذكورة أعلاه ، توجد خاصية موازية لعدم المساواة في المتجهات.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 نظريات الوجود العام

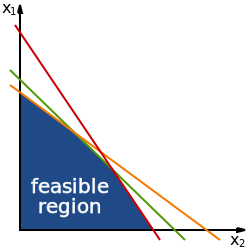
قالب:قسم غير معروف لنظام عام من عدم المساواة متعدد الحدود ، يمكن للمرء أن يجد شرطا للحل في الوجود. أولاً ، يمكن اختزال أي نظام لعدم المساواة متعدد الحدود إلى نظام من عدم المساواة من الدرجة الثانية عن طريق زيادة عدد المتغيرات والمعادلات (على سبيل المثال ، عن طريق تعيين مربع من متغير يساوي متغير جديد). يمكن كتابة تباين متعدد الحدود واحد من الدرجة الثانية في متغيرات 'n' - 1 كـ

خطأ رياضيات (خطأ في الصيغة): {\displaystyle X ^ T A X \ geq 0، }

حيث X هي متجه للمتغيرات خطأ رياضيات (خطأ في الصيغة): {\displaystyle X = (x، y، z، \ ldots، 1) ^ \ mathsf {T} } ، و 'A' 'مصفوفة. هذا له حل ، على سبيل المثال ، عندما يكون هناك عنصر إيجابي واحد على الأقل في الخط الرئيسي لـ "A".

يمكن كتابة أنظمة عدم المساواة من حيث المصفوفات "A" و "B" و "C" وما إلى ذلك ، ويمكن كتابة شروط وجود حلول كتعبيرات معقدة فيما يتعلق بهذه المصفوفات. يخبرنا حل عدم المساواة متعدد الحدود في اثنين من المتغيرات ما إذا كانت منطقتان مخروطي المقطع تتداخلان أو داخل بعضهما البعض. الحل العام غير معروف ، لكن يمكن استخدام هذا الحل من الناحية النظرية لحل المشكلات التي لم يتم حلها مثل مشكلة رقم التقبيل. ومع ذلك ، ستكون الظروف معقدة للغاية بحيث تتطلب قدراً كبيراً من وقت الحوسبة أو خوارزميات ذكية.

 أنظر أيضا

• Binary relation
• Bracket (mathematics), for the use of similar ‹ and › signs as brackets
• Fourier–Motzkin elimination
• Inclusion (set theory)
• Inequation
• Interval (mathematics)
• List of inequalities
• List of triangle inequalities
• Partially ordered set
• Relational operators, used in programming languages to denote inequality

 مصادر

• Hardy, G., Littlewood J. E., Pólya, G. (1999). Inequalities. Cambridge Mathematical Library, Cambridge University Press. ISBN 0-521-05206-8. {{cite book}}: no-break space character in |author= at position 25 (help)CS1 maint: multiple names: authors list (link)
• Beckenbach, E. F., Bellman, R. (1975). An Introduction to Inequalities. Random House Inc. ISBN 0-394-01559-2. {{cite book}}: no-break space character in |author= at position 15 (help)CS1 maint: multiple names: authors list (link)
• Drachman, Byron C., Cloud, Michael J. (1998). Inequalities: With Applications to Engineering. Springer-Verlag. ISBN 0-387-98404-6.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Grinshpan, A. Z. (2005), "General inequalities, consequences, and applications", Advances in Applied Mathematics 34 (1): 71–100, doi:10.1016/j.aam.2004.05.001 
• Murray S. Klamkin. "'Quickie' inequalities" (PDF). Math Strategies.
• Arthur Lohwater (1982). "Introduction to Inequalities". Online e-book in PDF format.
• Harold Shapiro (2005). "Mathematical Problem Solving". The Old Problem Seminar. Kungliga Tekniska högskolan.
• "3rd USAMO". Archived from the original on 2008-02-03.
• Pachpatte, B. G. (2005). Mathematical Inequalities. North-Holland Mathematical Library. Vol. 67 (first ed.). Amsterdam, The Netherlands: Elsevier. ISBN 0-444-51795-2. ISSN 0924-6509. MR 2147066. Zbl 1091.26008. {{cite book}}: no-break space character in |first= at position 3 (help)
• Ehrgott, Matthias (2005). Multicriteria Optimization. Springer-Berlin. ISBN 3-540-21398-8.
• Steele, J. Michael (2004). The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities. Cambridge University Press. ISBN 978-0-521-54677-5.

 وصلات خارجية

• Hazewinkel, Michiel, ed. (2001), "Inequality", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• Graph of Inequalities by Ed Pegg, Jr.
• AoPS Wiki entry about Inequalities