مبرهنة تشيڤا
مبرهنة تشيڤا هي مبرهنة شهيرة في الهندسة الابتدائية.
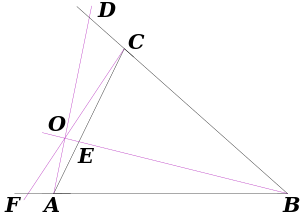
من أجل مثلث ABC ونقاط D، E، F تقع على أضلاعه الثلاثة BC، CA، AB على الترتيب، تنص المبرهنة أن المستقيمات الثلاثة AD، BE، CF تتقاطع في نقطة مشتركة فقط وفقط إذا كانت النسبة التالية محققة:
وهناك صيغة مثلثية مشابهة أيضاً لمبرهنة سيفا، وذلك بأن المستقيمات الثلاثة AD،BE،CF تتقاطع إذا وفقط إذا تحقق:
تم برهان هذه المبرهنة من قبل جوڤاني تشيڤا في أعماله في عام 1678، ولكن كانت المبرهنة قد برهنت سابقاً من قبل العالم المؤتمن بن هود ملك سرقسطة في القرن الحادي عشر ميلادي.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
مراجع
- Grünbaum, Branko; Shephard, G. C. (1995), "Ceva, Menelaus and the Area Principle", Mathematics Magazine 68 (4): 254–268, http://links.jstor.org/sici?sici=0025-570X(199510)68%3A4%3C254%3ACMATAP%3E2.0.CO%3B2-0.
- J. B. Hogendijk, "Al-Mutaman ibn Hűd, 11the century kin of Saragossa and brilliant mathematician," Historia Mathematica 22 (1995) 1-18.
- Landy, Steven. A Generalization of Ceva's Theorem to Higher Dimensions. The American Mathematical Monthly, Vol. 95, No. 10 (Dec., 1988), pp. 936-939
- Masal'tsev, L. A. (1994) "Incidence theorems in spaces of constant curvature." Journal of Mathematical Sciences, Vol. 72, No. 4
- Wernicke, Paul. The Theorems of Ceva and Menelaus and Their Extension. The American Mathematical Monthly, Vol. 34, No. 9 (Nov., 1927), pp. 468-472