مبرهنة الألوان الأربعة

تلوين رباعي لخريطة حقيقية لولايات الولايات المتحدة تتجاهل ألوان الماء والبلدان الأخرى والكتابة).

مبرهنة الألوان الأربعة تنص على أنه يمكن لأي مستوى مقسّم إلى عدّة مناطق أن يلّون فقط بأربعة ألوان على أكثر تقدير, بحيث لا تلون منطقتان متجاورتان (لهما نفس الحدود) بنفس اللون، إلا في حالة تشاركهما في نقطة واحدة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

صياغة دقيقة للمبرهنة

Example of a map of Azerbaijan with non-contiguous regions

برهان منطقي

الفكرة العامة هو أن أي منطقة إذا كانت محاطة بعدد زوجي من المناطق فإننا نحتاج فقط لعدد 3 ألوان لتلوين المنطقة والمناطق المحيطة بها مباشرة - لون 1 للمنطقة نفسها - لون 2 لأول منطقة من المناطق المحيطة بها ثم لون 3 للمنطقة التالية من المناطق المحيطة وهكذا بالتبادل 2 ثم 3 وتنتهي أخر منطقة باللون 3 دون وجود منطقتين متجاورتين لهما نفس اللون .
أم إذا كانت المنطقة محاطة بعدد فردي من المناطق فنحتاج لأربعة ألوان فقط واللون الرابع لتلوين المنطقة الأخيرة والتي ترتيبها فردي حيث تليها المنطقة الأولي والتي ترتيبها فردي أيضا ومن ثم فإن أقصي عدد من الألوان المختلفة والتي تلزم لتلوين خريطة تضم عددا من المناطق هو أربعة ألوان فقط

البرهنة

ملخص أفكار البرهنة

Suppose v, e, and f are the number of vertices, edges, and regions. Euler's formula states v − e + f = 2. This together with the fact that each edge is shared by two regions, 2e = 3f, can be used to show 6v − 2e = 12. Now, the degree of a vertex is the number of edges abutting it. If v_n is the number of vertices of degree n and D is the maximum degree of any vertex,

6v-2e=6\sum _{i=1}^{D}v_{i}-\sum _{i=1}^{D}iv_{i}=\sum _{i=1}^{D}(6-i)v_{i}=12.

But since 12 > 0 and 6 − i ≤ 0 for all i ≥ 6, this demonstrates that there is at least one vertex of degree 5 or less.

Recall the formula above:

\sum _{i=1}^{D}(6-i)v_{i}=12.

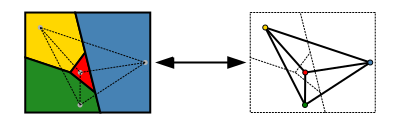
من الممكن، ربط مشكل الألوان الأربعة، بمشكلة تلوين المخطط

نربط كل رسم, بمخطط عادي كل رأس يمثل منطقة, و يتم ربط الرؤوس التي تمثل مناطق لها نفس الحدود.

مخطط مرتبط بالخريطة

هذا يعني أن تلوين الخريطة مرتبط بتلوين المخطط المستوي المرتبط بالخريطة. و هكذا تكون خوارزمية التلوين كما يلي:

خوارزمية التلوين

ملاحظة: نستعمل الأرقام 1، 2، 3 و 4 للتعبير عن الألوان الأربعة.

رسم المخطط المستوي المرتبط بالخريطة.
نأخد مثلثا و نلون رؤوسه بالألوان 1، 2 و 3.
انطلاقا من هذا المثلث نحاول تلوين القمم باستعمال الألوان الثلاث الأولى.(سيكون التلوين في هذه الحالة إجباريا).
نأخد مثلثا آخر غير ملون ونعيد المرحلتين رقم 2 و 3.
نستعمل اللون الرابع فقط في الحالة التي تكون فيها قمة ما مرتبطة في آن واحد بثلاثة قمم ذات 3 ألوان مختلفة.
نعود للخريطة ونلونها حسب الألوان المحصل عليها.

نقوض خاطئة


This map has been colored with five colors...	...and it is necessary to change at least four of the ten regions to obtain a coloring with only four colors.

تعميمات

By joining the single arrows together and the double arrows together, one obtains a torus with seven mutually touching regions; therefore seven colors are necessary

This construction shows the torus divided into the maximum of seven regions, every one of which touches every other.

Alternatively, for an orientable surface the formula can be given in terms of the genus of a surface, g:

p=\left\lfloor {\frac {7+{\sqrt {1+48g}}}{2}}\right\rfloor

(Weisstein).

This formula, the Heawood conjecture, was conjectured by P.J. Heawood in 1890 and proven by Gerhard Ringel and J. T. W. Youngs in 1968. The only exception to the formula is the Klein bottle, which has Euler characteristic 0 (hence the formula gives p = 7) and requires 6 colors, as shown by P. Franklin in 1934 (Weisstein).

For example, the torus has Euler characteristic χ = 0 (and genus g = 1) and thus p = 7, so no more than 7 colors are required to color any map on a torus. The Szilassi polyhedron is an example that require seven colors.

A Möbius strip also requires six colors (Weisstein).

انظر أيضاً

Graph coloring: the problem of finding optimal colorings of graphs that are not necessarily planar.
Grötzsch's theorem: triangle-free planar graphs are 3-colorable.
Hadwiger–Nelson problem: how many colors are needed to color the plane so that no two points at unit distance apart have the same color?
List of sets of four countries that border one another: Contemporary examples of national maps requiring four colors

المراجع

Allaire, F. (1997), "Another proof of the four colour theorem—Part I", Proceedings, 7th Manitoba Conference on Numerical Mathematics and Computing, Congr. Numer. 20: 3–72
Appel, Kenneth; Haken, Wolfgang; Koch, John (1977), "Every Planar Map is Four Colorable", Illinois Journal of Mathematics 21: 439–567
Appel, Kenneth; Haken, Wolfgang (October 1977), "Solution of the Four Color Map Problem", Scientific American 237 (4): 108–121, doi:10.1038/scientificamerican1077-108
Appel, Kenneth; Haken, Wolfgang (1989), Every Planar Map is Four-Colorable, Providence, RI: American Mathematical Society, ISBN 0821851039
Cayley, Arthur (1879), "On the colourings of maps", Proc. Royal Geographical Society (Blackwell Publishing) 1 (4): 259–261, doi:10.2307/1799998, http://jstor.org/stable/1799998
Gonthier, Georges (2008), "Formal Proof--The Four-Color Theorem", Notices of the American Mathematical Society 55 (11): 1382–1393, http://www.ams.org/notices/200811/tx081101382p.pdf
Gonthier, Georges (2005), A computer-checked proof of the four colour theorem, unpublished, http://research.microsoft.com/~gonthier/4colproof.pdf
Hadwiger, Hugo (1943), "Über eine Klassifikation der Streckenkomplexe", Vierteljschr. Naturforsch. Ges. Zürich 88: 133–143 .
Heawood, P. J. (1890), "Map-Colour Theorem", Quarterly Journal of Mathematics, Oxford 24: 332–338
O'Connor; Robertson (1996), The Four Colour Theorem, MacTutor archive, http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/The_four_colour_theorem.html
Pegg, Ed, Jr. (2002), "Book Review: The Colossal Book of Mathematics", Notices of the American Mathematical Society 49 (9): 1084–1086, http://www.ams.org/notices/200209/rev-pegg.pdf
Ringel, G.; Youngs, J.W.T. (1968), "Solution of the Heawood Map-Coloring Problem", Proc. Nat. Acad. Sci. USA 60: 438–445, doi:10.1073/pnas.60.2.438
Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1996), "Efficiently four-coloring planar graphs", Efficiently four-coloring planar graphs, STOC'96: Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, ACM Press, pp. 571–575, doi:10.1145/237814.238005
Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1997), "The Four-Colour Theorem", J. Combin. Theory Ser. B 70 (1): 2–44, doi:10.1006/jctb.1997.1750
Saaty, Thomas; Kainen, Paul (1986), The Four Color Problem: Assaults and Conquest, New York: Dover Publications, ISBN 0-486-65092-8
Swart, ER (1980), "The philosophical implications of the four-color problem", American Mathematical Monthly (Mathematical Association of America) 87 (9): 697–702, doi:10.2307/2321855, http://www.joma.org/images/upload_library/22/Ford/Swart697-707.pdf
Thomas, Robin (1998), "An Update on the Four-Color Theorem", Notices of the American Mathematical Society 45 (7): 848–859, http://www.ams.org/notices/199807/thomas.pdf
Thomas, Robin (1995), The Four Color Theorem, http://www.math.gatech.edu/~thomas/FC/fourcolor.html
Thomas, Robin, Recent Excluded Minor Theorems for Graphs, p. 14, http://people.math.gatech.edu/~thomas/PAP/bcc.pdf
Eric W. Weisstein, Blanuša snarks at MathWorld.
Eric W. Weisstein, Map coloring at MathWorld.
Wilson, Robin (2002), Four Colors Suffice, London: Penguin Books, ISBN 0-691-11533-8

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

وصلات خارجية