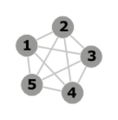
مخطط مستوي
في المخططات، المخطط المستوي هو المخطط الذي يقبل تمثيلا في المستوى، بحيث لا يتقاطع أي ارتباطين من المخطط.
معايير المخطط المستوي
حسب Kuratowski يكون المخطط مستويا إذا لم يتضمن زمرة من الرتبة 5، أو مخطط ثنائي كامل من الرتبة 3 (انظر الصور).
- Graphe K32C3.png
مخطط ثنائي كامل من الرتبة 3
وجوه مخطط مستوي
ليكن G مخطط مستوي، الوجه F هو أكبر منطقة من المستوى محددة بمجموعة ارتباطات G و لا تتضمن أيا منها.
ليكن G مخطط مستوي، و a عدد ارتباطات G. إذن :
صيغة أولير
تعاريف
- المسار ذو الطول r هو سلسلة من القمم المرتبطة مع أصل السبيل و طرفه.
- يكون المخطط متصلا إذا وُجد مسار بين كل قمتين من G.
- المسار المغلق هو حالة .
- الشجرة هي مخطط متصل بدون أي مسار مغلق.
تمهيدة
كل مخطط متصل يمكن الحصول عليه بإضافة عدة قمم لشجرة (لها نفس عدد القمم).
صيغة أولير للمخططات المستوية المتصلة
ليكن G مخطط مستوي متصل. ليكن n عدد قمم a, G عدد ارتباطاته و f عدد وجوهه. إذن: n − a + f = 2
المعايير
تحديد المعايير التي تمكن من معرفة ان كان مخطط ما مستويا. ليكن G مخطط مستوي متصل. ليكن n عدد قمم a, G عدد ارتباطاته:
- في حالة وجود مثلثات.
- في حالة عدم وجود مثلثات.
This article may include material from Wikimedia licensed under CC BY-SA 4.0. Please comply with the license terms.