قضيب مهتز

القضبان المهتزة verges هي أجسام صلبة، أحد أبعادها أكبر بكثير من البعدين الآخرين. وعلى الرغم من أن هذا التعريف غير دقيق، لكنه يسمح بتمييز القضيب عن الصفيحة، حيث يكون بعد واحد ـ هو الثخانة ـ أصغر بكثير من البعدين الآخرين اللذين يكونان متقاربين، تُعد المسطرة المعدنية ـ على سبيل المثال ـ قضيباً يمكن تحريض اهتزازات فيه بالنقر. ويلاحظ بسهولة أن ارتفاع الصوت الناتج يختلف كثيراً، حسبما يكون النقر في اتجاه طول المسطرة أو عمودياً عليها. في الحالة الأولى، تُحرَّض بشكلٍ رئيسي الاهتزازات الطولانية، وفي الثانية تُحرَّض الاهتزازات العرضانية. ويمكن ـ إضافة إلى هذين النوعين ـ توليد اهتزازات فَتْل في القضيب، فتصبح المسألة أعقد، ويولِّد النقر عامة مزيجاً من هذه الأنواع المختلفة من الاهتزازات. يساعد اتجاه النقر على تفضيل هذا النوع أو ذاك من الاهتزازات.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الترددات الذاتية

لايمكن حساب الترددات الذاتية fréquences propres لاهتزاز القضبان إلا في الحالات البسيطة، عندما تكون الاهتزازات طولانيةً صِرفة أو عرضانية صِرفة، ويكون للقضيب شكل هندسي بسيط أيضاً، أي له مقطع ثابت عمودي على البعد الكبير، وهذا المقطع مستطيل الشكل أو دائري. ويمكن تمييز الحالات الآتية:

 الاهتزازات الطولانية لقضيب ذي مقطع ثابت

تقابل الأنماط الذاتية modes propres للاهتزازات كل الأمواج المستقرة التي يمكنها أن تنشأ في القضيب، آخذين بالاعتبار الشروط عند طرفي القضيب حيث يوجد بطن عند الطرف الحر وعقدة عند الطرف المثبّت، وتكون النتائج مماثلة تماماً لحالة الأنابيب الصوتية. أما في حالة قضبان حرة الطرفين، فتتكون سلسلة من الأصوات الجزئية من كل توافقيات تردد أساسي V/2L حيث L طول القضيب وV سرعة انتشار الأمواج الطولانية على طول القضيب (حيث E معامل يونغ و ρ الكتلة الحجمية لمادة القضيب). وإذا كان القضيب مثبتاً من طرف وحراً من الطرف الآخر، فلا تنشأ عندها إلا التوافقيات الفردية لتردد أساسي V/4L. يشار إلى أنه لا وجود عملياً لآلة موسيقية تستخدم الاهتزازات الطولانية للقضبان المهتزة.

 الاهتزازات العرضانية لقضيب ذي مقطع ثابت

الشكل (1) أنماط اهتزاز القضبان

تكون أنماط الاهتزاز الذاتية في هذه الحالة مستقرة أيضاً، ولكن النتائج ليست بسيطة كتلك الموافقة للاهتزازات الطولانية، إذ لا تكون المسافة بين العقد والبطون ثابتة، كما أنها لا تساوي كسراً بسيطاً من طول القضيب. ولا تتعلق ترددات الأصوات الجزئية بطول القضيب فقط وبالمادة التي صُنع منها وبالشروط الحدّية، ولكنها تتعلق أيضاً بشكل مقطعه العرضي وأبعاده. فضلاً عن ذلك؛ فإن هذه الترددات تتناسب عكساً مع مربع طول القضيب L. ففي حالة قضيب مقطعه مستطيل، تكون الترددات متناسبة مع ثخانة القضيب e في الاتجاه الموازي للاهتزاز، وتكون متناسبة مع نصف القطر في حالة قضيب أسطواني. يمكن إذاً كتابة تردد الأصوات الجزئية لمثل هذه القضبان على الشكل:

حيث A(k) وB(k) معاملان يتعلقان بكل ما لم يؤخذ بالحسبان حتى اليوم، أي المادة المكوّنة للقضيب والشروط عند الطرفين؛ ترمز k إلى مرتبة الأصوات الجزئية. يبين (الشكل 1) كيفية توزع بطون الاهتزازات وعقدها في حالة الأنماط الأولى للاهتزازات العرضانية للقضبان حرة الطرفين أو المثبتة في طرف والحرة في الطرف الآخر. تتناسب الأعداد N لكل نمط مع المعاملين A(k) وB(k). تبين هذه الأعداد أن سلسلة الأصوات الجزئية لا تؤلف سلسلة توافقية، على عكس ما يحدث في حالة الأوتار المهتزة والأنابيب الصوتية والقضبان المحرَّضة طولانياً.

 الآلات الموسيقية ذات القضبان المهتزة

الشكل (2) الآلة الموسيقية الخشبية

الشكل (3) علبة الموسيقى

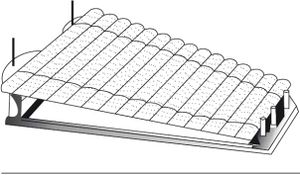
في الخشبية xylophone الظاهرة في (الشكل 2)، تثبت صفائح من الخشب (من هنا جاءت التسمية) أو من الزجاج أو من المعدن بسلكين فولاذيين عند نقاط تشكل عقد النمط الأول لاهتزاز القضبان الحرة الطرفين. تطرق الصفائح بالمطرقة في منتصف الصفائح.

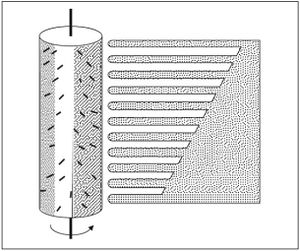
في علبة الموسيقى (الشكل 3)، تأخذ القضبان شكل صفائح مقتطعة ذات أطوال مختلفة في صفيحة معدنية، ويكون للمجموع شكل المشط. تهتز القضبان بوساطة رؤوس مدببة مثبتة ناظمياً على أسطوانة معدنية. يمكن بتوزيع مناسب لهذه الرؤوس عزف أنغام محدّدة عندما تدور الأسطوانة. وبإزاحة الأسطوانة قليلاً يمكن عزف أنغامٍ مختلفة.

 انظر أيضا

• آلة موسيقية