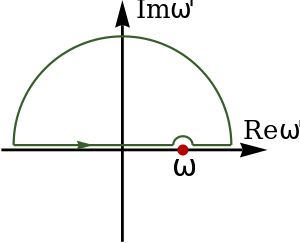
علاقات كرامرز-كرونيگ
فى علمي الرياضيات والفيزياء تصف علاقات كرامرز-كرونيگ العلاقة بين الجزء الحقيقي والتخيلي في تصنيف معين من الدوال التى لها قيم معقدة. العلاقات مسماة على شرف رالف كرونيگ[1] وهندريك أنتوني كرامرز.[2] وفي الرياضيات، تُعرف تلك العلاقات بأسماء مبرهنة سوخوتسكي-پلملي وتحول هيلبرت.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
الصياغة
متطلبات الدالة التى سوف يتم التطبيق عليها يمكن أن تفسر كما لو كانت نفس المعادلة تمثل تحول فوريير للعمليات الفيزيائية الخطية والغير نظامية. فلو كتبنا:
- ,
حيث , و هى قيم حقيقة دوال "لها تصرف جيد"، وعندها تصبح العلاقة:
- .
وترتبط علاقة كرامرز-كرونيگ بتحول هيلبرت، وغالبا ما تطبق على سماحية( المواد. وعموما, يجب ملاحظة أنه في هذه الحالة يكون:
- ,
حيث هى القابلية الكهربية للمادة. ويمكن تفسير هذه القابلية مثل تحول فوريير للإستقطاب المتعلق-بالزمن في المادة بعد حدوث ميل صغير للنبضات الكهربية, وبمعنى أخر إستجابة الإستقطاب للدفعات.
برهنة ذات صلة من نطاق الزمن
انظر أيضاً
- تحول هيلبرت Hilbert transform
- مبرهنة سوخوتسكي-پلملي Sokhotski–Plemelj theorem
- Linear response function
- تشتت Dispersion (optics)
المصادر
- ويكيبيديا الإنجليزية.
- ^ R. de L. Kronig (1926). "On the theory of the dispersion of X-rays". J. Opt. Soc. Am. 12: 547–557. doi:10.1364/JOSA.12.000547.
- ^ H.A. Kramers (1927). "La diffusion de la lumiere par les atomes". Atti Cong. Intern. Fisici, (Transactions of Volta Centenary Congress) Como. 2: 545–557.