تحول هيلبرت

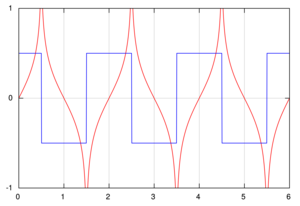
تحول هلبرت، بالأحمر، لـموجة مربعة، بالأزرق.

تحوّل هلبرت Hilbert transform هي عملية خطية تستخدم في الرياضيات وعمليات معالجة الإشارة. تحويل هيلبرت سمي بعدما قدم ديفيد هيلبرت حلا لحالة خاصة من معضلة ريمان وهيلبرت

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 جدول تحولات هلبرت مختارة

الإشارة $u(t)\,$	تحول هلبرت $H(u)(t)$
$\sin(t)$	$-\cos(t)$
$\cos(t)$	$\sin(t)$
$\exp(it)$	$-i\exp(it)$
$\exp(-it)$	$i\exp(-it)$
$1 \over t^{2}+1$	$t \over t^{2}+1$
$\exp(-t^{2})$	$2\pi ^{-1/2}F(t)$ (see Dawson function)
Sinc function $\sin(t) \over t$	$1-\cos(t) \over t$
Rectangular function $\sqcap (t)$	${1 \over \pi }\ln \left\vert {t+{1 \over 2} \over t-{1 \over 2}}\right\vert$
Dirac delta function $\delta (t)$	${1 \over \pi t}$
Characteristic Function $\chi _{[a,b]}(t)$	${{\frac {1}{\pi }}\ln \left\vert {\frac {t-a}{t-b}}\right\vert }$

ملاحظات

An extensive table of Hilbert transforms is available (King 2009). Note that the Hilbert transform of a constant is zero.

 تحول هلبرت المتقطع

Figure 1: Filter whose frequency response is bandlimited to about 95% of the Nyquist frequency

Figure 2: Hilbert transform filter with a highpass frequency response

Figure 3.

Figure 4. The Hilbert transform of cos(ωt) is sin(ωt). This figure shows sin(ωt) and two approximate Hilbert transforms computed by the MATLAB library function, hilbert(·)

Figure 5. Discrete Hilbert transforms of a cosine function, using piecewise convolution

For a discrete function,  $u[n],$  with discrete-time Fourier transform (DTFT),  $U(\omega ),$  and discrete Hilbert transform  ${\hat {u}}[n],$  the DTFT of  ${\hat {u}}[n]$  in the region  −π < ω <  π is given by:

$\operatorname {DTFT} \displaystyle ({\hat {u}})=U(\omega )\cdot (-i\cdot \operatorname {sgn}(\omega )).$

The inverse DTFT, using the convolution theorem, is:

${\begin{aligned}{\hat {u}}[n]&=\scriptstyle {DTFT}^{-1}\displaystyle (U(\omega ))\ *\ \scriptstyle {DTFT}^{-1}\displaystyle (-i\cdot \operatorname {sgn}(\omega ))\\&=u[n]\ *\ {\frac {1}{2\pi }}\int _{-\pi }^{\pi }(-i\cdot \operatorname {sgn}(\omega ))\cdot e^{i\omega n}d\omega \\&=u[n]\ *\ \underbrace {{\frac {1}{2\pi }}\left[\int _{-\pi }^{0}i\cdot e^{i\omega n}d\omega -\int _{0}^{\pi }i\cdot e^{i\omega n}d\omega \right]} _{h[n]},\end{aligned}}$

حيث:

$h[n]\ {\stackrel {\mathrm {def} }{=}}\ {\begin{cases}0,&{\text{for }}n{\text{ even}}\\{\frac {2}{\pi n}}&{\text{for }}n{\text{ odd}},\end{cases}}$

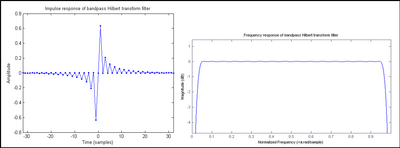
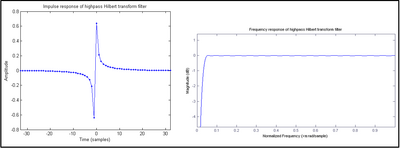
which is an infinite impulse response (IIR). When the convolution is performed numerically, an FIR approximation is substituted for h[n], as shown in Figure 1. An FIR filter with an odd number of anti-symmetric coefficients is called Type III, which inherently exhibits responses of zero magnitude at frequencies 0 and Nyquist, resulting in this case in a bandpass filter shape. A Type IV design (even number of anti-symmetric coefficients) is shown in Figure 2. Since the magnitude response at Nyquist does not drop out, it approximates an ideal Hilbert transformer a little better than the odd-tap filter. However:

• A typical (i.e. properly filtered and sampled) u[n] sequence has no useful components at the Nyquist frequency.
• The Type IV impulse response requires a ½ sample shift in the h[n] sequence. That causes the zero-valued coefficients to become non-zero, as seen in Figure 2. So a Type III design is potentially twice as efficient as Type IV.
• The group delay of a Type III design is an integer number of samples, which facilitates aligning ${\hat {u}}[n]$ with $u[n],$ to create an analytic signal. The group delay of Type IV is halfway between two samples.

The MATLAB function, hilbert(u,N), convolves a u[n] sequence with the periodic summation:

$h_{N}[n]\ {\stackrel {\text{def}}{=}}\ \sum _{m=-\infty }^{\infty }h[n-mN]={\begin{cases}0,&{\text{for }}n{\text{ even}},\\{\frac {2}{N\tan(n\pi /N)}}&{\text{for }}n{\text{ odd}},\end{cases}}$

and returns one cycle (N samples) of the periodic result in the imaginary part of a complex-valued output sequence. The convolution is implemented in the frequency domain as the product of the array  $\scriptstyle {DFT}\displaystyle \left(u[n]\right)$  with samples of the −i•sgn(ω) distribution (whose real and imaginary components are all just 0 or ±1). Figure 3 compares a half-cycle of h_N[n] with an equivalent length portion of h[n]. Given an FIR approximation for  $h[n],$ denoted by  ${\tilde {h}}[n],$  substituting  $\scriptstyle {DFT}\displaystyle \left({\tilde {h}}[n]\right)$  for the −i•sgn(ω) samples results in an FIR version of the convolution.

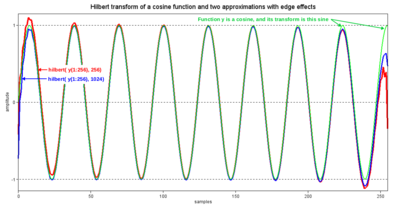
The real part of the output sequence is the original input sequence, so that the complex output is an analytic representation of u[n]. When the input is a segment of a pure cosine, the resulting convolution for two different values of N is depicted in Figure 4 (red and blue plots). Edge effects prevent the result from being a pure sine function (green plot). Since h_N[n] is not an FIR sequence, the theoretical extent of the effects is the entire output sequence. But the differences from a sine function diminish with distance from the edges. Parameter N is the output sequence length. If it exceeds the length of the input sequence, the input is modified by appending zero-valued elements. In most cases, that reduces the magnitude of the differences. But their duration is dominated by the inherent rise and fall times of the h[n] impulse response.

An appreciation for the edge effects is important when a method called overlap-save is used to perform the convolution on a long u[n] sequence. Segments of length N are convolved with the periodic function:

${\tilde {h}}_{N}[n]\ {\stackrel {\text{def}}{=}}\ \sum _{m=-\infty }^{\infty }{\tilde {h}}[n-mN].$

When the duration of non-zero values of  ${\tilde {h}}[n]$  is M < N, the output sequence includes N − M + 1 samples of  ${\hat {u}}.$  M-1 outputs are discarded from each block of N, and the input blocks are overlapped by that amount to prevent gaps.

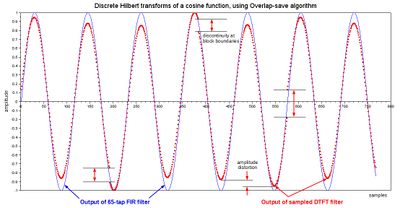
Figure 5 is an example of using both the IIR hilbert() function and the FIR approximation. In the example, a sine function is created by computing the Discrete Hilbert transform of a cosine function, which was processed in four overlapping segments, and pieced back together. As the FIR result (blue) shows, the distortions apparent in the IIR result (red) are not caused by the difference between h[n] and h_N[n] (green and red in Fig 3). The fact that h_N[n] is tapered (windowed) is actually helpful in this context. The real problem is that it's not windowed enough. Effectively, M = N, whereas the overlap-save method needs M < N.

 انظر أيضا

• Analytic signal
• Harmonic conjugate
• Hilbert spectroscopy
• Hilbert transform in the complex plane
• Hilbert–Huang transform
• علاقات كرامرز-كرونيگ
• Single-sideband signal
• Singular integral operators of convolution type

 وصلات خارجية

• Derivation of the boundedness of the Hilbert transform
• Mathworld Hilbert transform — Contains a table of transforms
• Analytic Signals and Hilbert Transform Filters
• Eric W. Weisstein, Titchmarsh theorem at MathWorld.
• Johansson, Mathias. "The Hilbert transform" (PDF). Archived from the original (PDF) on 2012-02-05. a student level summary of the Hilbert transformation.
• "GS256 Lecture 3: Hilbert Transformation" (PDF). Archived from the original (PDF) on 2012-02-27. an entry level introduction to Hilbert transformation.