عدد كاتالان
في الرياضيات، تشكل الأعداد الكاتلانية إنگليزية: Catalan numbers سلسلة من الأعداد الطبيعية التي تظهر في العديد من مسائل العد والتي غالباً ما تحتوي على أجسام معرفة بشكل عودي. تم تسمية الأعداد الكاتلانية على اسم الرياضياتي البلجيكي أوجين شارل كاتالان (1814 - 1894).
يعطى العدد الكاتلاني ذو الترتيب n بشكل مباشر باستخدام الصيغة العاملية التالية:
حيث تعطى الأعداد الأولى من سلسلة الأعداد الكاتلانية بالشكل: 1 - 1 - 2 - 5 - 14 - 42 - 132 - 429 - 1430 - 4862 - 16796 - 58786 - 208012 - ...
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
خصائص
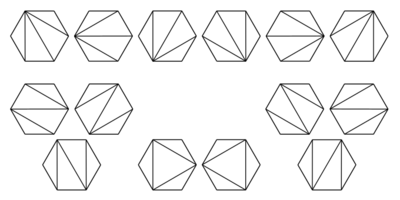
تطبيقات في التوافيق
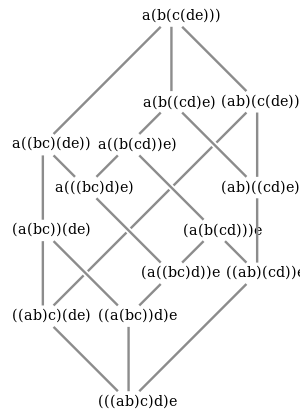
برهان الصيغة
البرهان الأول
البرهان الثاني
البرهان الثالث
البرهان الرابع
البرهان الخامس
مصفوفة هنكل
The n×n Hankel matrix whose (i, j) entry is the Catalan number Ci+j−2 has determinant 1, regardless of the value of n. For example, for n = 4 we have
Moreover, if the indexing is "shifted" so that the (i, j) entry is filled with the Catalan number Ci+j−1 then the determinant is still 1, regardless of the value of n. For example, for n = 4 we have
Taken together, these two conditions uniquely define the Catalan numbers.
التاريخ
انظر أيضا
|
|
Notes
الهامش
- Conway and Guy (1996) The Book of Numbers. New York: Copernicus, pp. 96–106.
- Gardner, Martin (1988), Time Travel and Other Mathematical Bewilderments, New York: W.H. Freeman and Company, pp. 253–266 (Ch. 20), ISBN 0-7167-1924-X
- Koshy, Thomas (2008), Catalan Numbers with Applications, Oxford University Press, ISBN 0-19-533454-X, http://www.amazon.com/Thomas-Koshy/e/B001H6NZT4/ref=ntt_athr_dp_pel_1
- Koshy, Thomas & Zhenguang Gao (2011) "Some divisibility properties of Catalan numbers", Mathematical Gazette 95:96-102.
- Larcombe, P.J. (1999) "The 18th century Chinese discovery of the Catalan numbers", Mathematical Spectrum 32:5-7.
- Stanley, Richard P. (1999), Enumerative combinatorics. Vol. 2, Cambridge Studies in Advanced Mathematics, 62, Cambridge University Press, ISBN 978-0-521-56069-6, http://www-math.mit.edu/~rstan/ec/
- Egecioglu, Omer (2009), A Catalan-Hankel Determinant Evaluation, http://www.cs.ucsb.edu/~omer/DOWNLOADABLE/catalan_hankel09.pdf
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
وصلات خارجية
- Stanley, Richard P. (1998) (PDF), Catalan addendum to Enumerative Combinatorics, Volume 2, http://www-math.mit.edu/~rstan/ec/catadd.pdf
- Eric W. Weisstein, Catalan Number at MathWorld.
- Dickau, Robert M.: Catalan numbers Further examples.
- Davis, Tom: Catalan numbers. Still more examples.
- Schmidthammer, Jürgen: Catalan-Zahlen Zulassungsarbeit zum Staatsexamen (PDF-File; 7,05 MB)
- "Equivalence of Three Catalan Number Interpretations" from The Wolfram Demonstrations Project [1]