رمز مصادقة الرسالة

لعدم الخلط مع Media access control أو Media access control.

في التعمية، رمز مصادقة الرسالة message authentication code (MAC)، المعروف أحياناً باسم العلامة، هو جزء قصير من المعلومات المستخدمة في مصادقة رسالة - بمعنى آخر، لتأكيد أن الرسالة جاءت من المرسل المعلن (أصالتها) ولم يتم تغييرها. تحمي قيمة MAC تكامل بيانات الرسالة، بالإضافة إلى مصداقيتها، من خلال السماح للمحققين (الذين يمتلكون أيضاً المفتاح السري) باكتشاف أي تغييرات في محتوى الرسالة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

تعاريف

بشكل غير اصطلاحي، يتكون نظام رمز مصادقة الرسائل من ثلاث خوارزميات:

  • تختار خوارزمية توليد المفاتيح مفتاحاً من فضاء المفتاح بشكل عشوائي.
  • تقوم خوارزمية التوقيع بإرجاع العلامة بكفاءة مع إعطاء المفتاح والرسالة.
  • تتحقق خوارزمية التحقق بكفاءة من صحة الرسالة المعطاة للمفتاح والعلامة. أي، يتم قبول الإرجاع عندما لا يتم العبث بالرسالة والعلامة أو تزويرهما، وبخلاف ذلك يتم إرجاع مرفوض.

للحصول على رمز مصادقة آمن للرسالة غير القابلة للتزوير، يجب أن يكون من غير المجدي حسابياً حساب علامة صالحة للرسالة المعينة دون معرفة المفتاح، حتى لو كان في أسوأ الحالات، نفترض أن الخصم يمكنه تزوير علامة أي رسالة باستثناء الرسالة المحددة.[1]

بشكل اصطلاحي، نظام رمز مصادقة الرسالة (MAC) عبارة عن ثلاثة خوارزميات فعالة[2] (G, S, V) تحقق:

  • يعطي G (مولد المفاتيح) المفتاح k في الإدخال 1n، حيث يمثل n پارامتر الأمان.
  • يخرج S (التوقيع) علامة t على المفتاح k وسلسلة الإدخال x.
  • مخرجات V (التحقق) مقبولة أو مرفوضة على المدخلات: المفتاح k والسلسلة x والعلامة t.

يجب أن تستوفي S و V ما يلي:

Pr [ k ← G(1n), V( k, x, S(k, x) ) = مقبول ] = 1.[3]

يكون MAC غير مزور إذا كان لكل خصم فعال A

Pr [ k ← G(1n), (x, t) ← AS(k, · )(1n), x ∉ Query(AS(k, · ), 1n), V(k, x, t) = مقبول] < negl(n),

حيث يشير AS(k, · ) إلى أن A له حق الوصول إلى أوراكل S(k, · ) والاستعلام (AS(k, · ), 1n) تشير مجموعة الاستعلامات الموجودة على S التي أجراها A، والتي تعرف n. من الواضح أننا نطالب بعدم تمكن أي خصم من الاستعلام مباشرة عن السلسلة x الموجودة في S، لأنه بخلاف ذلك يمكن بسهولة الحصول على علامة صالحة بواسطة هذا الخصم.[4]


الحماية

بينما تشبه دوال MAC دوال دالة تجزئة التعمية، فإنها تمتلك متطلبات أمان مختلفة. لكي تعتبر وظيفة MAC آمنة، يجب أن تقاوم التزوير الوجودي تحت هجوم النص المبرمج. هذا يعني أنه حتى إذا كان المهاجم لديه وصول إلى أوراكل الذي يمتلك المفتاح السري وينشئ MAC للرسائل التي يختارها المهاجم، فلا يمكن للمهاجم تخمين MAC للرسائل الأخرى (التي لم يتم استخدامها للاستعلام عن أوراكل) دون إجراء كميات غير مجدية من الحسابات.

تختلف MAC عن التوقيعات الرقمية حيث يتم إنشاء قيم MAC والتحقق منها باستخدام نفس المفتاح السري. هذا يعني أن المرسل والمستقبل للرسالة يجب أن يتفقوا على نفس المفتاح قبل بدء الاتصالات، كما هو الحال مع التشفير المتناظر. للسبب نفسه، لا توفر MAC خاصية عدم الرفض التي تقدمها التوقيعات على وجه التحديد في حالة وجود مفتاح سري مشترك على مستوى الشبكة: أي مستخدم يمكنه التحقق من MAC قادر أيضاً على توليد MAC للرسائل الأخرى. في المقابل، يتم إنشاء التوقيع الرقمي باستخدام المفتاح الخاص لزوج المفاتيح، وهو تعمية المفتاح العام.[2] نظراً لأن هذا المفتاح الخاص لا يمكن الوصول إليه إلا لحامله، فإن التوقيع الرقمي يثبت أن المستند لم يوقعه غير ذلك المالك. وبالتالي، فإن التوقيعات الرقمية تقدم عدم الرفض. ومع ذلك، يمكن توفير عدم الرفض من خلال الأنظمة التي تربط معلومات استخدام المفتاح بشكل آمن بمفتاح MAC؛ نفس المفتاح في حوزة شخصين، لكن أحدهما لديه نسخة من المفتاح يمكن استخدامها لإنشاء MAC بينما يمتلك الآخر نسخة من المفتاح في وحدة أمان الأجهزة التي تسمح فقط بالتحقق من MAC. يتم ذلك بشكل شائع في مجال التمويل.[بحاجة لمصدر]

Message integrity codes

كثيراً ما يتم استبدال المصطلح رمز سلامة الرسالة (MIC) بمصطلح MAC، خاصة في الاتصالات،[5]لتمييزه عن استخدام MAC بمعنى عنوان ماك (لـ عنوان التحكم في الوصول إلى الوسائط). ومع ذلك، يستخدم بعض المؤلفين[6] MIC للإشارة إلى ملخص الرسالة، والتي تختلف عن MAC - لا تستخدم خلاصة الرسالة مفاتيح سرية. يعني هذا النقص في الأمان أن أي رسالة موجزة مخصصة لاستخدام قياس تكامل الرسائل يجب أن تكون مشفرة أو محمية بطريقة أخرى من العبث. يتم إنشاء خوارزميات ملخص الرسائل بحيث تنتج رسالة معينة دائماً نفس الرسالة على افتراض استخدام نفس الخوارزمية لتوليد كليهما. على العكس من ذلك، تم تصميم خوارزميات MAC لإنتاج مطابقة MACs مطابقة فقط إذا تم إدخال نفس الرسالة والمفتاح السري و متجه تهيئة في نفس الخوارزمية. لا تستخدم خلاصات الرسائل المفاتيح السرية، وعند أخذها من تلقاء نفسها، فهي بالتالي مقياس أقل موثوقية لسلامة الرسالة من أجهزة MAC. نظراً لأن أجهزة MAC تستخدم مفاتيح سرية، فلا يلزم بالضرورة تشفيرها لتوفير نفس مستوى الضمان.

يوصي RFC 4949 بتجنب المصطلح "رمز تكامل الرسالة" (MIC)، وبدلاً من ذلك استخدام "المجموع الاختباري"، "رمز كشف الخطأ"، " التجزئة"، "التجزئة ذات المفاتيح " أو " رمز مصادقة الرسالة " أو " المجموع الاختباري المحمي ".

التنفيذ

يمكن إنشاء خوارزميات MAC من بدائل التشفير الأخرى، مثل دوال تجزئة التعمية (كما في حالة HMAC) أو من التشفير الكتلي خوارزميات ( OMAC، CCM، GCM، و PMAC). ومع ذلك، فإن العديد من خوارزميات MAC الأسرع مثل UMAC - VMAC و Poly1305-AES مبنية على أساس التجزئة العامة.[7]

تعد خوارزميات التجزئة ذات المفاتيح الفعلية مثل SipHash أيضاً بحكم تعريفها MAC؛ يمكن أن تكون أسرع من أجهزة MAC القائمة على التجزئة الشاملة.[8]

بالإضافة إلى ذلك، يمكن لخوارزمية MAC أن تجمع بشكل مدروس بين اثنين أو أكثر من أساسيات التعمية، وذلك للحفاظ على الحماية حتى لو تبين لاحقاً أن أحدهما معرض للخطر. على سبيل المثال، في أمن طبقة النقل (TLS)، يتم تقسيم إدخال البيانات إلى نصفين وتتم معالجة كل منها باستخدام تجزئة اولية بسيطة مختلفة (SHA-1 و SHA-2) ثم XORed معاً لإخراج MAC.

المعايير

توجد معايير مختلفة تحدد خوارزميات MAC. وتشمل هذه:

  • FIPS PUB 113 مصادقة بيانات الحاسب،[9] والتي تم سحبها عام 2002،[10] حيث تحدد خوارزمية قائمة على DES.
  • FIPS PUB 198-1 The Keyed-Hash Message Authentication Code (HMAC)[11]
  • ISO/IEC 9797-1 آليات استخدام التشفير الكتلي[12]
  • ISO/IEC 9797-2 الآليات التي تستخدم دالة تجزئة مخصصة[13]
  • ISO/IEC 9797-3 الآليات التي تستخدم دالة تجزئة شاملة[14]
  • ISO/IEC 29192-6 رموز مصادقة الرسائل-ذات تعمية خفيفة الوزن[15]

تحدد المواصفة القياسية ISO / IEC 9797-1 و -2 النماذج والخوارزميات العامة التي يمكن استخدامها مع أي كتلة تشفير أو دالة تجزئة ومجموعة متنوعة من الپارامترات المختلفة. تسمح هذه النماذج والپارامترات بتحديد المزيد من الخوارزميات المحددة من خلال تعيين الپارامترات. على سبيل المثال، خوارزمية FIPS PUB 113 مكافئة وظيفياً لخوارزمية MAC 1 / ISO / IEC 9797-1 مع طريقة الحشو 1 وخوارزمية تشفير الكتلي DES.

مثال على استخدام MAC

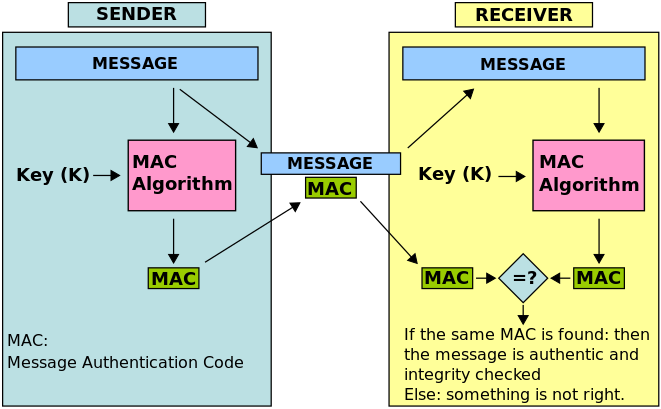
MAC.svg

[16]في هذا المثال، يقوم مرسل الرسالة بتشغيلها من خلال خوارزمية MAC لإنتاج علامة بيانات MAC. ثم يتم إرسال الرسالة وعلامة MAC إلى جهاز الاستقبال. يقوم جهاز الاستقبال بدوره بتشغيل جزء الرسالة من الإرسال من خلال نفس خوارزمية MAC باستخدام نفس المفتاح، مما ينتج عنه علامة بيانات MAC ثانية. يقارن جهاز الاستقبال بعد ذلك علامة MAC الأولى المستلمة في الإرسال بعلامة MAC الثانية التي تم إنشاؤها. إذا كانت متطابقة، يمكن للمستقبل أن يفترض بأمان أن الرسالة لم يتم تغييرها أو العبث بها أثناء الإرسال (سلامة البيانات).

ومع ذلك، للسماح للمستقبل بالقدرة على اكتشاف هجوم إعادة التشغيل، يجب أن تحتوي الرسالة نفسها على بيانات تؤكد أن هذه الرسالة نفسها لا يمكن إرسالها إلا مرة واحدة (مثل الطابع الزمني أو الرقم التسلسلي أو استخدام mac لمرة واحدة). وبخلاف ذلك، يمكن للمهاجم - حتى دون فهم محتواها - تسجيل هذه الرسالة وتشغيلها في وقت لاحق، مما ينتج عنه نفس النتيجة مثل المرسل الأصلي.

MAC لمرة واحدة

توفر التجزئة الشاملة وعلى وجه الخصوص دوال التجزئة المستقلة زوجياً رمز مصادقة رسالة آمنة طالما تم استخدام المفتاح مرة واحدة على الأكثر. يمكن اعتبار هذا MAC لمرة واحدة للمصادقة.[17]

يتم تحديد أبسط دالة تجزئة مستقلة زوجياً من خلال المفتاح العشوائي key = (a,b)، وتكون علامة MAC للرسالة m محسوبة كـ tag = (am + b) mod p، حيث يكون p عدداً أولياً.

بشكل عام، توفر دوال تجزئة k-المستقلة رمز مصادقة رسالة آمنة طالما تم استخدام المفتاح أقل من k مرة لـ k - طرق دوال التجزئة المستقلة.

تمت أيضاً مناقشة رموز مصادقة الرسائل ومصادقة أصل البيانات في إطار عمل التعمية الكمية. على النقيض من مهام التعمية الأخرى، مثل توزيع المفاتيح، لفئة واسعة إلى حد ما من أجهزة MAC الكمومية، فقد تبين أن الموارد الكمية لا تقدم أي ميزة على أجهزة MAC الكلاسيكية الآمنة غير المشروطة لمرة واحدة. [18]

انظر أيضاً

ملاحظات

  1. ^ The strongest adversary is assumed to have access to the signing algorithm without knowing the key. However, her final forged message must be different from any message she chose to query the signing algorithm before. See Pass's discussions before def 134.2.
  2. ^ أ ب Theoretically, an efficient algorithm runs within probabilistic polynomial time.
  3. ^ Pass, def 134.1
  4. ^ Pass, def 134.2
  5. ^ IEEE 802.11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications (PDF). (2007 revision). IEEE-SA. 12 June 2007. doi:10.1109/IEEESTD.2007.373646. ISBN 978-0-7381-5656-9.
  6. ^ Fred B Schneider, Hashes and Message Digests, Cornell University
  7. ^ . "VMAC: Message Authentication Code using Universal Hashing".
  8. ^ Jean-Philippe Aumasson & Daniel J. Bernstein (2012-09-18). "SipHash: a fast short-input PRF" (PDF).
  9. ^ "FIPS PUB 113 Computer Data Authentication". Archived from the original on 2011-09-27. Retrieved 2010-10-10.
  10. ^ "Federal Information Processing Standards Publications, Withdrawn FIPS Listed by Number". Archived from the original on 2010-08-01. Retrieved 2010-10-10.
  11. ^ رمز مصادقة الرسالة ذات التجزئة المفتاحية (HMAC)
  12. ^ ISO/IEC 9797-1 Information technology — Security techniques — Message Authentication Codes (MACs) — Part 1: Mechanisms using a block cipher
  13. ^ ISO/IEC 9797-2 Information technology — Security techniques — Message Authentication Codes (MACs) — Part 2: Mechanisms using a dedicated hash-function
  14. ^ ISO/IEC 9797-3 Information technology — Security techniques — Message Authentication Codes (MACs) — Part 3: Mechanisms using a universal hash-function
  15. ^ ISO/IEC 29192-6 Information technology — Lightweight cryptography — Part 6: Message authentication codes (MACs)
  16. ^ "Mac Security Overview", Mac® Security Bible, Wiley Publishing, Inc., 2011-11-01, pp. 1–26, doi:10.1002/9781118257739.ch1, ISBN 9781118257739 
  17. ^ Simmons, Gustavus (1985). "Authentication theory/coding theory". Advances in Cryptology: Proceedings of CRYPTO 84. Berlin: Springer. pp. 411–431. ISBN 00000000. {{cite book}}: Check |isbn= value: length (help)
  18. ^ Nikolopoulos, Georgios M.; Fischlin, Marc (2020). "Information-Theoretically Secure Data Origin Authentication with Quantum and Classical Resources". Cryptography (in الإنجليزية). 4 (4): 31. arXiv:2011.06849. doi:10.3390/cryptography4040031. S2CID 226956062.{{cite journal}}: CS1 maint: unflagged free DOI (link)

المراجع


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

وصلات خارجية

  1. ^ 11-12-20C8
تمّ الاسترجاع من "https://www.marefa.org/w/index.php?title=رمز_مصادقة_الرسالة&oldid=2279281"