دالة محدبة

دالة محدبة على فترة.

دالة (باللون الأسود) محدبة لو، وفقط لو، المنطقة فوق رسمها البياني (باللون الأخضر) كانت فئة محدبة.

الدالة بالأزرق هي دالة محدّبة على طول محور الأعداد الحقيقية: كل مستقيم يصل بين أي نقطتين على الرسم البياني للدالة يقع فوق الرسم البياني للدالة.

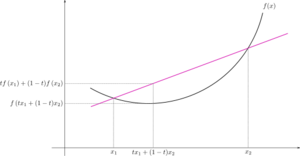
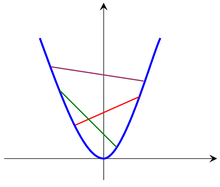
تدعى دالة رياضية (بمتغير واحد) دالة محدّبة في مقطع ما إذا كان الخط المستقيم الذي يصل بين أي نقطتين على الرسم البياني للدالة في هذا المقطع يقع فوق الرسم البياني للدالة نفسها. على سبيل المثال فإنّ الدالّة $f\left(x\right)=x^{2}$ هي دالة محدّبة على طول محور الأعداد الحقيقية، كما يظهر في الرسم. وتجدر الإشارة إلى أنّ مفهوم التحدب والتقعر قد يكون عكس المفهوم اللغوي أو التصويري (فقد يظن البعض أن شكل الرسم البياني هو مقعر وليس محدب).

بالإمكان تطوير تعريف الدالة المحدبة ليشمل دوال بأكثر من متغير واحد، بل وأي دالة ذات قيم حقيقية معرّفة في نطاق يشكل مجموعة محدبة في فضاء اتجاهي ما.

للدوال المحدّبة استعمالات عديدة وهامّة، خاصة في مجالات التحليل الدالي والاستمثال المحدب، وتظهر في عدة متراجحات مهمّة، منها متراجحة ينسن.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

تعريف

إنّ الدالة ذات القيم الحقيقية $f\left(x\right)$ تدعى دالة محدبة إذا تحقّق لكل نقطتين $x$ و $y$ في نطاق الدالة C ولكل $\lambda$ في المجال [0,1] ما يلي:

f\left(\lambda x+\left(1-\lambda \right)y\right)\leq \lambda f\left(x\right)+\left(1-\lambda \right)f\left(y\right)

هذا وتدعى الدالة $f$ محدبة تمامًا إذا تحقّق:

f\left(\lambda x+\left(1-\lambda \right)y\right)<\lambda f\left(x\right)+\left(1-\lambda \right)f\left(y\right)

لكل $\lambda$ في المجال (0,1) ولكل $x\leq y$ .

أمّا إذا كانت الدالة $-f\left(x\right)$ هي دالة محدبّة فتدعى الدالة $\ f$ دالة مقعرة.

ويظهر تفسير كون الدالة أحادية المتغير محدّبة إذا كان الخط المستقيم الذي يصل بين أي نقطتين على رسمها البياني يقع فوق الرسم البياني، يظهر من المتراجحة أعلاه، إذ أنّه إذا كانت $z=\lambda x+\left(1-\lambda \right)y$ هي نقطة تقع بين x وy (تذكير: $\lambda \in \left[0,1\right]$ )، فإنّ:

g\left(z\right)=\lambda f\left(x\right)+(1-\lambda )f\left(y\right)

،

حيث أنّ $g$ هي معادلة الخط المستقيم (أي $g\left(x\right)=f\left(x\right)$ و $g\left(y\right)=f\left(y\right)$ ).

خواص تحليلية

إذا كانت f وg دالتين محدّبتين، فإنّ الدالتين: $m(x)=\operatorname {max} \{f(x),g(x)\}$ و $h\left(x\right)=f\left(x\right)+g\left(x\right)$ هما محدبتان كذلك؛
إذا كانت f وg دالتين محدّبتين، وكانت $g$ دالة غير تنازلية، فإنّ $h\left(x\right)=g\left(f\left(x\right)\right)$ ؛
تحدّب الدالة لا يتغير إثر تحويلات أفينيّة على المتغيّر، أي أنّه إذا كانت f هي دالة محدبة وكان $x\in \mathbb {R} ^{n}$ ، فإنّ $g\left(y\right)=f\left(Ay+b\right)$ هي دالة محدبة، حيث $b\in \mathbb {R} ^{n}$ ، $y\in \mathbb {R} ^{m}$ ، $A\in \mathbb {R} ^{n\times m}$ ؛

أمثلة

الدالة $f\left(x\right)=x^{2}$ هي دالة محدبة تمامًا إذ أنّ المشتق الثاني للدالة موجب لكل x: $f\,''\left(x\right)=2>0$ .

إنّ المشتق الثاني للدالة $f\left(x\right)=x^{3}$ هو $6x$ أي أنّه غير سالب في المجموعة $\{x\geq 0\}$ ، ولذا فإنّ f محدّبة هناك، وغير موجب في المجموعة $\{x\leq 0\}$ ، أي أنّ الدالة مقعرة هناك.

دالة القيمة المطلقة $f(x)=|x|$ محدبة، بالرغم من أن ليس لديها مشتقة عند النقطة x = 0. لذا فهي ليست محدبة دوماً.
الدالة $f(x)=|x|^{p}$ حين يكون 1 ≤ p هي محدبة.
الدالة الأسية $f(x)=e^{x}$ محدبة. It is also strictly convex, since $f''(x)=e^{x}>0$ ، ولكنها ليست قوية التحدب إذ أن المشتقة الثانية يمكن أن تكون عشوائياً قريبة من الصفر. وبشكل أكثر عموماً، الدالة $g(x)=e^{f(x)}$ هي محدبة لوغاريتمياً if ƒ هي دالة محدبة.
الدالة ƒ في النطاق [0,1] معرفة كالتالي: ƒ(0) = ƒ(1) = 1, ƒ(x) = 0 for 0 < x < 1 is convex; it is continuous on the open interval (0, 1), but not continuous at 0 and 1.
The function x³ has second derivative 6x; thus it is convex on the set where x ≥ 0 and concave on the set where x ≤ 0.
Every linear transformation taking values in $\mathbb {R}$ is convex but not strictly convex, since if f is linear, then $f(a+b)=f(a)+f(b).$ This statement also holds if we replace "convex" by "concave".
Every affine function taking values in $\mathbb {R}$ , i.e., each function of the form $f(x)=a^{T}x+b$ , is simultaneously convex and concave.
Every norm is a convex function, by the triangle inequality and positive homogeneity.
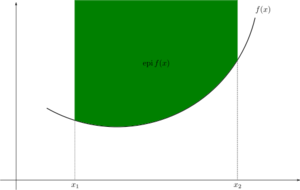
If ƒ is convex, the perspective function $g(x,t)=tf(x/t)$ is convex for t > 0.
Examples of functions that are monotonically increasing but not convex include $f(x)={\sqrt {x}}$ and g(x) = log(x).
Examples of functions that are convex but not monotonically increasing include $h(x)=x^{2}$ and $k(x)=-x$ .
The function ƒ(x) = 1/x², with f(0) = +∞, is convex on the interval (0, +∞) and convex on the interval (-∞,0), but not convex on the interval (-∞, +∞), because of the singularity at x = 0.