حلقة (هندسة رياضية)

شكل الحلقة

في الرياضيات، وتحديداً في الهندسة الرياضية يعطى شكل الحلقة في المستوي على شكل قرص مفرغ بدائرة مشتركة المركز مع مركز القرص. تعادل الحلقة طوبولوجياً إسطوانة مفرغة $S^{1}\times (0,1)$ والمستوي المثقوب.

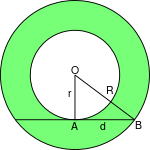
تعطى مساحة الحلقة بأخذ فرق مساحة الدائرتين ذاتي أنصاف الأقطار R و r على الشكل التالي:

$A=\pi (R^{2}-r^{2})\,.$

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انظر أيضاً

• إسطوانة