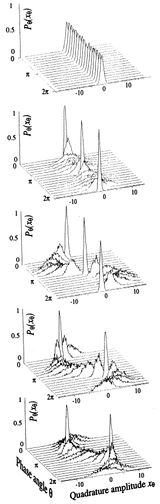
حالة متماسكة معتصرة

هذه بذرة مقالة عن موضوع علمي تحتاج للنمو والتحسين، ساهم في إثرائها بالمشاركة في تحريرها.

الحالة المتماسكة المعتصرة Squeezed coherent state هي كل حالة ضمن فضاء هلبرت في ميكانيكا الكم والتي تحقق مبدأ الإرتياب بأدنى قيمة لجداء الإرتيابات أي :

\Delta x\Delta p={\frac {\hbar }{2}}

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

أمثلة للحالات المعتصرة

Depending on at which phase the state's quantum noise is reduced, one can distinguish amplitude-squeezed and phase-squeezed states or general quadrature squeezed states. If no coherent excitation exists the state is called a squeezed vacuum. The figures below give a nice visual demonstration of the close connection between squeezed states and Heisenberg's uncertainty relation: Diminishing the quantum noise at a specific quadrature (phase) of the wave has as a direct consequence an enhancement of the noise of the complementary^{[بحاجة لتوضيح]} quadrature, that is, the field at the phase shifted by $\pi /2$ .

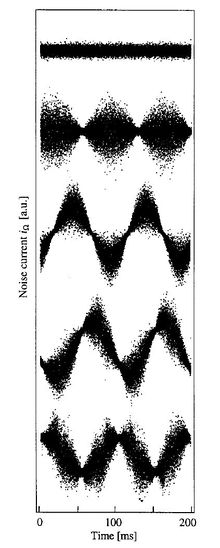Figure 1: Measured quantum noise of the electric field of different squeezed states depends on the phase of the light field. For the first two states a 3π-interval is shown; for the last three states, belonging to a different set of measurements, it is a 4π-interval.^[1] (source: external link 1)

Figure 2: Oscillating wave packets of the five states.

Figure 3: Wigner functions of the five states. The ripples are due to experimental inaccuracies.

من أعلى:

حالة فارغة
حالة فارغة معتصرة
حالة طور معتصر
حالة معتصرةى عشوائية
Amplitude-squeezed state

توزيعات أعداد الفوتونات وتوزيعات الأطوار للحالات المتماسكة المعتصرة

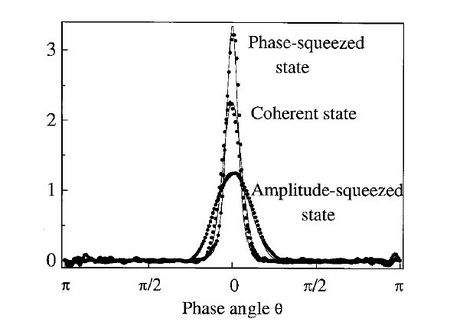
الزاوية المعتصرة، that is the phase with minimum quantum noise, has a large influence on the photon number distribution of the light wave and its phase distribution as well.

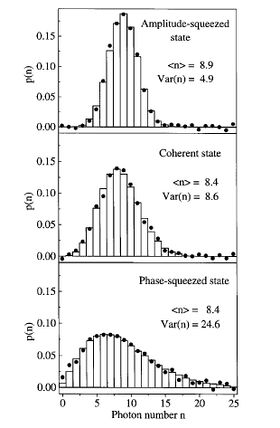Figure 4: Experimental photon number distributions for an amplitude-squeezed state, a coherent state, and a phase squeezed state reconstructed from measurements of the quantum statistics. Bars refer to theory, dots to experimental values.^[1] (source: link 1)

Figure 5: Pegg-Barnett phase distribution of the three states.

For amplitude squeezed light the photon number distribution is usually narrower than the one of a coherent state of the same amplitude resulting in sub-Poissonian light, whereas its phase distribution is wider. The opposite is true for the phase-squeezed light, which displays a large intensity (photon number) noise but a narrow phase distribution. Nevertheless the statistics of amplitude squeezed light was not observed directly with photon number resolving detector due to experimental difficulty.^[2]

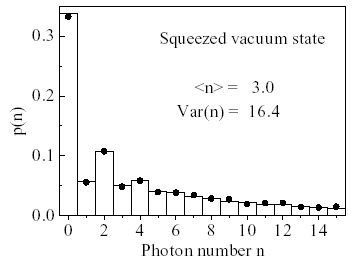
Figure 4: Reconstructed and theoretical photon number distributions for a squeezed-vacuum state.^[1] (source: link 1)

For the squeezed vacuum state the photon number distribution displays odd-even-oscillations. This can be explained by the mathematical form of the squeezing operator, that resembles the operator for two-photon generation and annihilation processes. Photons in a squeezed vacuum state are more likely to appear in pairs.

انظر أيضاً

الهامش

^ ^أ ^ب ^ت G. Breitenbach, S. Schiller, and J. Mlynek, "Measurement of the quantum states of squeezed light", Nature, 387, 471 (1997)
^ Entanglement evaluation with Fisher information - http://arxiv.org/pdf/quant-ph/0612099

وصلات خارجية

[Breitenbach-1] أ ^ب ^ت G. Breitenbach, S. Schiller, and J. Mlynek, "Measurement of the quantum states of squeezed light", Nature, 387, 471 (1997)

[2] Entanglement evaluation with Fisher information - http://arxiv.org/pdf/quant-ph/0612099

[1]

[2]