توزيع ثنائي الحدين

"Binomial model" redirects here. For the binomial model in options pricing, see Binomial options pricing model.

انظر أيضاً: Negative binomial distribution

Binomial distribution

Probability mass function
Cumulative distribution function
الترميز	$B(n,p)$
الوسائط	$n\in \{0,1,2,\ldots \}$ – number of trials $p\in [0,1]$ – success probability for each trial
الحامل	$k\in \{0,1,\ldots ,n\}$ – number of successes
PMF	${\binom {n}{k}}p^{k}(1-p)^{n-k}$
CDF	$I_{1-p}(n-k,1+k)$
المتوسط	$np$
أوسط	$\lfloor np\rfloor$ or $\lceil np\rceil$
منوال	$\lfloor (n+1)p\rfloor$ or $\lceil (n+1)p\rceil -1$
تباين	$np(1-p)$
تخالف	${\frac {1-2p}{\sqrt {np(1-p)}}}$
تدبب زائد	${\frac {1-6p(1-p)}{np(1-p)}}$
الاعتلاج	${\frac {1}{2}}\log _{2}\left(2\pi enp(1-p)\right)+O\left({\frac {1}{n}}\right)$ in shannons. For nats, use the natural log in the log.
MGF	$(1-p+pe^{t})^{n}$
CF	$(1-p+pe^{it})^{n}$
PGF	$G(z)=[(1-p)+pz]^{n}$
معلومات فيشر	$g_{n}(p)={\frac {n}{p(1-p)}}$ (for fixed $n$)

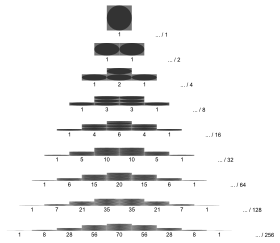
Binomial distribution for $p=0.5$
with n and k as in Pascal's triangle

The probability that a ball in a Galton box with 8 layers (n = 8) ends up in the central bin (k = 4) is $70/256$.

توزيع احتمالي ثنائي هو توزيع لتجربة عشوائية لها ناتجان فقط أحدهما نجاح التجربة والآخر فشلها ويكون الشرط الأساسي أن احتمال النجاح لا يتأثر بتكرار التجربة ، أمثلة : رمي قطعة نقود ، الإحصاءات أو الأسئلة التي تعتمد الإجابة لا أو نعم.

بتعبير آخر التوزيع الاحتمالي ثنائي الحد هو تكرار لتجربة برنولي (انظر توزيع برنولي).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 خصائص التوزيع الثنائي

يتميز التوزيع الثنائى بعدة خصائص هي:

1. تتكون التجربة من أكثر من محاولة. إذا تكونت التجربة من محاولة واحدة ،فإننا في تجربة توزيع برنولي.
2. استقلال المحاولات عن بعضها البعض أي ثبات احتمال النجاح p ومن ثم احتمال الفشل q.
3. هذه المحاولات جميعا متماثلة ومستقلة.
4. احتمال النجاح ثابت في كل محاولة.

${\begin{aligned}F(k;n,p)&=\Pr(X\leq k)\\&=I_{1-p}(n-k,k+1)\\&=(n-k){n \choose k}\int _{0}^{1-p}t^{n-k-1}(1-t)^{k}\,dt.\end{aligned}}$

Some closed-form bounds for the cumulative distribution function are given below.

 Example

Suppose a biased coin comes up heads with probability 0.3 when tossed. What is the probability of achieving 0, 1,..., 6 heads after six tosses?

$\Pr(0{\text{ heads}})=f(0)=\Pr(X=0)={6 \choose 0}0.3^{0}(1-0.3)^{6-0}=0.117649$

$\Pr(1{\text{ heads}})=f(1)=\Pr(X=1)={6 \choose 1}0.3^{1}(1-0.3)^{6-1}=0.302526$

$\Pr(2{\text{ heads}})=f(2)=\Pr(X=2)={6 \choose 2}0.3^{2}(1-0.3)^{6-2}=0.324135$

$\Pr(3{\text{ heads}})=f(3)=\Pr(X=3)={6 \choose 3}0.3^{3}(1-0.3)^{6-3}=0.18522$

$\Pr(4{\text{ heads}})=f(4)=\Pr(X=4)={6 \choose 4}0.3^{4}(1-0.3)^{6-4}=0.059535$

$\Pr(5{\text{ heads}})=f(5)=\Pr(X=5)={6 \choose 5}0.3^{5}(1-0.3)^{6-5}=0.010206$

$\Pr(6{\text{ heads}})=f(6)=\Pr(X=6)={6 \choose 6}0.3^{6}(1-0.3)^{6-6}=0.000729$

 Mean

If X ~ B(n, p), that is, X is a binomially distributed random variable, n being the total number of experiments and p the probability of each experiment yielding a successful result, then the expected value of X is:

$\operatorname {E} [X]=np.$

For example, if n = 100, and p = 1/4, then the average number of successful results will be 25.

Proof: We calculate the mean, μ, directly calculated from its definition

$\mu =\sum _{i=0}^{n}x_{i}p_{i},$

and the binomial theorem:

${\begin{aligned}\mu &=\sum _{k=0}^{n}k{\binom {n}{k}}p^{k}(1-p)^{n-k}\\&=np\sum _{k=0}^{n}k{\frac {(n-1)!}{(n-k)!k!}}p^{k-1}(1-p)^{(n-1)-(k-1)}\\&=np\sum _{k=1}^{n}{\frac {(n-1)!}{((n-1)-(k-1))!(k-1)!}}p^{k-1}(1-p)^{(n-1)-(k-1)}\\&=np\sum _{k=1}^{n}{\binom {n-1}{k-1}}p^{k-1}(1-p)^{(n-1)-(k-1)}\\&=np\sum _{\ell =0}^{n-1}{\binom {n-1}{\ell }}p^{\ell }(1-p)^{(n-1)-\ell }&&{\text{with }}\ell :=k-1\\&=np\sum _{\ell =0}^{m}{\binom {m}{\ell }}p^{\ell }(1-p)^{m-\ell }&&{\text{with }}m:=n-1\\&=np(p+(1-p))^{m}\\&=np\end{aligned}}$

 History

This distribution was derived by James Bernoulli. He considered the case where p = r/(r + s) where p is the probability of success and r and s are positive integers. Blaise Pascal had earlier considered the case where p = 1/2.

 See also

• Logistic regression
• Multinomial distribution
• Negative binomial distribution
• Beta-binomial distribution
• Binomial measure, an example of a multifractal measure.
• Statistical mechanics

 مراجع

• https://www.jmasi.com/ehsa/prob/binomail.htm
• https://faculty.ksu.edu.sa/mhmmurad/DocLib4/%D8%A7%D9%84%D9%88%D8%AD%D8%AF%D8%A9%20%D8%A7%D9%84%D8%AE%D8%A7%D9%85%D8%B3%D8%A9%20%D8%A7%D9%84%D8%AC%D8%B2%D8%A1%20%D8%A7%D9%84%D8%A7%D8%AB%D8%A7%D9%86%D9%8A.pdf