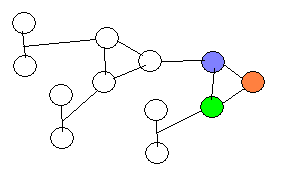
تلوين مخطط بثلاثة ألوان

مسألة NP كاملة
قابلية الإرضاء 3SAT NAE OIT
تلوين مخطط تلوين مخطط بثلاثة ألوان تلوين مخطط مستو بثلاثة ألوان
زمرة كبرى
مسار هاملتونياني
عدل

تلوين المخطط باستعمال ثلاثة ألوان هي مسألة مشتقة من المسألة العامة تلوين مخطط و تتم باستعمال ثلاثة ألوان فقط، و رغم ذلك فهي مسألة NP كاملة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 تلوين مخطط بثلاثة ألوان مسألة كاملة

انطلاقا من SAT نحصل على مخطط عادي غير موجه، حيث يكون للصيغة حل إذا و فقط إذا كان هناك تلوين بثلاثة ألوان فقط. بعبارة أوضح حل SAT يحل مشكلة التلوين و حل مشكلة التلوين تحل SAT.

 الاختصار

gadjet 3COL

يتم من SAT لكل صيغة نربطها بمخطط عادي غير موجه، طريقة إنشائه كما يلي:

1. لكل متغيرين متقابلين $x\,$ و $\lnot x$ نرسم قمتين مرتبطتين، $U_{x}\,$ خاصة ب $x\,$ و $U_{\lnot x}$ خاصة ب $\lnot x$.
2. لكل رمز $\lor$ (أول رمز)، نرسم مثلث قممه $A_{1}$ و $B_{1}$ و $C_{1}$. و تسمى A رأس المثلث.
   1. في حالة وجود $x\,$ نربط القمة $U_{x}\,$ بB. أما في حالة وجود $\lnot x$ نربط القمة $U_{\lnot x}$ بB.
   2. بالنسبة للمتغير الثاني في الصيغة clause يتم ربط القمة التي تمثله بِC بنفس طريقة الربط مع B.
3. لكل رمز $\lor$ موالي(انطلاقا من ثاني رمز)، نرسم مثلث قممه $A_{2}$ و $B_{2}$ و $C_{2}$. نربط $A_{1}$ ب $B_{2}$. و $C_{2}$ بتمثيل المتغير الثالث.
4. المثلث الأخير و الذي يرمز لآخر رمز في الصيغة clause نسمي رأسه $A$ برأس العبارة.
5. في الأخير نضيف قمتين مرتبطتين الأولى محايدة $N$ و الثانية منعدمة $Z$:
   1. القمة $N$ مرتبطة برؤوس المثلثات و بالقمم التي تمثل المتغيرات.
   2. القمة $Z$ مرتبطة برؤوس العبارات.

الآن نستعمل للتلوين الأعداد 0 و 1 و 2، القمة N تلون ب2 و القمة z تلون ب3، هذا سيؤدي لتلوين جميع رؤوس العبارات باللون 1. و بعد انتهاء عملية التلوين، بالنسبة للصيغة نعطي للمتغير $x\,$ القيمة 1 في حالة كانت القمة $U_{x}\,$ ملونة باللون 1، بينما يأخد القيمة 0 في حالة كانت القمة $U_{x}\,$ ملونة باللون 0.