تلوين مخطط

| مسألة NP كاملة |
|---|
| زمرة كبرى |
| مسار هاملتونياني |
| عدل |
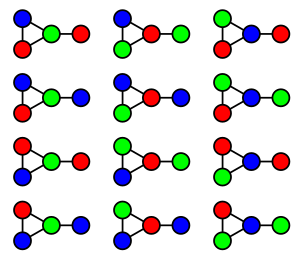
في مخطط عادي نريد تلوين كل رأس بلون، حيث لا نلون رأسين متجاورين بنفس اللون. المشكلة هي كيف نحدد أقل عدد ممكن من الألوان؟
التعريف والمصطلحات
تلوين الرؤوس
متعددة الحدود اللونية
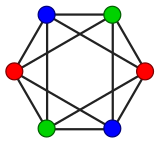
| الألوان المتاحة | 1 | 2 | 3 | 4 | … |
| عدد التلوينات | 0 | 0 | 12 | 72 | … |
The chromatic polynomial is a function P(G, t) that counts the number of t-colorings of G. As the name indicates, for a given G the function is indeed a polynomial in t. For the example graph, P(G, t) = t(t − 1)2(t − 2), and indeed P(G, 4) = 72.
The chromatic polynomial includes at least as much information about the colorability of G as does the chromatic number. Indeed, χ is the smallest positive integer that is not a root of the chromatic polynomial
| Triangle K3 | |
| Complete graph Kn | |
| Tree with n vertices | |
| Cycle Cn | |
| Petersen graph |
تلوين الأضلاع
خصائص
تحديد أقل عدد ممكن من الألوان يسمى عدد التلوين. و تحديد هذا العدد من المشاكل الكاملة, و هذا المشكل له علاقة قريبة جدا من مشكلة المخطط الكامل ضمن مخطط و مشكلة المخطط المستقر ضمن مخطط.
الخوارزميات
| تلوين المخطط | |
 | |
| القرار | |
| الاسم | Graph coloring, vertex coloring, k-coloring |
| المُدخل | Graph G with n vertices. Integer k |
| المُخرج | هل G تتيح تلوين رؤوس صحيح بعدد k من الألوان؟ |
| زمن الحساب | O(2 nn)[1] |
| التعقد | NP-complete |
| اختزال من | 3-Satisfiability |
| Garey–Johnson | GT4 |
| Optimisation | |
| الاسم | الرقم اللوني |
| المُدخل | المخطط G ذو n من الرؤوس. |
| المُخرج | χ(G) |
| التعقد | NP-hard |
| امكانية التقريب | O(n (log n)−3(log log n)2) |
| عدم امكانية التقريب | O(n1−ε) إلا إذا P = NP |
| مشكلة العـد | |
| الاسم | متعددة الحدود اللونية |
| المُدخل | المخطط G حيث n رؤوس. عدد صحيح k |
| المُخرج | العدد P (G,k) لعدد k مناسب -تلوينات G |
| زمن الحساب | O(2 nn) |
| التعقد | #P-complete |
| امكانية التقريب | FPRAS لحالات محددة |
| عدم امكانية التقريب | No PTAS إلا إذا P = NP |
زمن متعددة الحدود
تلوين طماع
التلوين بثلاثة ألوان
تلوين مخطط ما باستعمال ثلاثة ألوان فقط، هو أيضا مشكل كامل حيث يمكن اختصار أي مشكل من صنف المشاكل غير المحددة لمشكل التلوين بثلاثة ألوان.
التطبيقات
الجدولة الزمنية
تلوينات أخرى
نظرية رامسي
تلوينات أخرى
|
|
Coloring can also be considered for signed graphs and gain graphs.
انظر أيضاً
| تلوين مخطط
]].- Circular coloring
- Critical graph
- Cycle rank - Ordered chromatic number
- Graph homomorphism
- Mathematics of Sudoku
- Uniquely colorable graph
الهامش
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةbhk
وصلات خارجية
- Graph Coloring Page by Joseph Culberson (graph coloring programs)
- CoLoRaTiOn by Jim Andrews and Mike Fellows is a graph coloring puzzle
- GF-Graph Coloring Program [1]
- Links to Graph Coloring source codes
- Code for efficiently computing Tutte, Chromatic and Flow Polynomials by Gary Haggard, David J. Pearce and Gordon Royle